【基础练】人教版数学八年级下册 17.2勾股定理的逆定理

试卷日期：2025-04-03 考试类型：单元试卷

前去【出卷网】下载

一、选择题

1. 下列各组数据中，不是勾股数的是（）

A、3，4，5 B、5，12，13 C、6，8，10 D、2，3，4

查看试题解析
2. 下列各组数据中的三个数作为三角形的边长，其中能构成直角三角形的是（）

A、2，3，4 B、1， $\sqrt{2}$ ， $\sqrt{3}$ C、4，6，8 D、5，12，15

查看试题解析
3. $Δ A B C$ 中， $∠ A$ ， $∠ B$ ， $∠ C$ 的对边分别记为 $a$ ， $b$ ， $c$ ，下列条件不能判定 $Δ A B C$ 为直角三角形的是（）

A、 $∠ A + ∠ B = ∠ C$ B、 $∠ A = ∠ B = \frac{1}{2} ∠ C$ C、 $a : b : c = 3^{2} : 4^{2} : 5^{2}$ D、 $a : b : c = 5 : 12 : 13$

查看试题解析
4. 如果三角形三边长为5，m，n，且 $(m + n) (m - n) = 25$ ，那么此三角形形状为（）

A、锐角三角形 B、钝角三角形 C、等腰直角三角形 D、直角三角形

查看试题解析
5. 若三角形的三边长分别为a，b，c，且满足 ${(a - 2)}^{2} + |b - \sqrt{3}| + \sqrt{1 - c} = 0$ ，则这个三角形的形状为（）

A、钝角三角形 B、直角三角形 C、锐角三角形 D、等腰直角三角形

查看试题解析
6. 三角形的三边 $a$ ， $b$ ， $c$ 满足 $(a + b)^{2} - c^{2} = 2 a b$ ，则此三角形是（）

A、锐角三角形 B、直角三角形 C、钝角三角形 D、等边三角形

查看试题解析
7. 有六根细木棒，它们的长度分别是2，4，6，8，10，12（单位：cm），从中取出三根首尾顺次连接搭成一个直角三角形，则这三根木棒的长度分别为（）

A、2，4，8 B、4，8，10 C、6，8，10 D、8，10，12

查看试题解析
8. 如图，每个小正方形的边长都是1， $A$ ， $B$ ， $C$ 分别在格点上，则 $∠ A B C$ 的度数为（）.

A、 $30 °$ B、 $45 °$ C、 $50 °$ D、 $60 °$

查看试题解析
9. 我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题：“问有沙田一块，有三斜，其中小斜五里，中斜十二里，大斜十三里，欲知为田几何？“这道题讲的是：有一块三角形沙田，三条边长分别为 $5$ 里， $12$ 里， $13$ 里，则该沙田的面积为（）平方里．

A、 $30$ B、 $50$ C、 $60$ D、 $65$

查看试题解析

二、填空题

10. 在 $△ A B C$ 中，若 $A B = 17 ， A C = 8 ， B C = 15$ ，则根据可知 $∠ A C B =$

查看试题解析
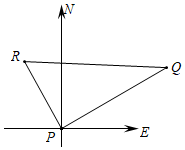
11. 已知三角形三边长分别为 $\sqrt{6}$ ， $\sqrt{6}$ ， $2 \sqrt{3}$ ，则此三角形的最大边上的高等于.

查看试题解析
12. 一个三角形的三边长的比为3：4：5，且其周长为60cm，则其面积为．

查看试题解析
13. 如图， $O A = 6$ ， $O B = 8$ ， $A B = 10$ ，点 $A$ 在点 $O$ 的北偏西 $40 °$ 方向，则点 $B$ 在点 $O$ 的方向．

查看试题解析
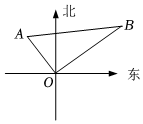14. 如图， $A D = 8$ ， $C D = 6$ ， $∠ A D C = 90 °$ ， $A B = 26$ ， $B C = 24$ ，该图形的面积等于．

查看试题解析

三、解答题

15. 在△ABC中，D是BC边上的点，AB＝13，AD＝12，BD＝5，AC＝15

(1)、求证：△ABD是直角三角形；

(2)、求DC的长．

查看试题解析
16. 如图，在正方形网格中，每个小正方形的边长都是 1.

(1)、填空： $A B =$ ， $C D =$ ；

(2)、在图中画出一条线段 $E F$ ，使得 $E F = \sqrt{10}$ ；判断以 $A B, C D, E F$ 三条线段为边能否构成直角三角形？请说明理由.

查看试题解析
17. 如图，在四边形 $A B C D$ 中， $∠ B = 90 °$ ， $A B = 16$ ， $B C = 12$ ， $A D = 21$ ， $C D = 29$ ．求四边形 $A B C D$ 的面积．

查看试题解析
18. 如图，一条伸直的橡皮筋 $A B$ 的两端被固定在水平桌面上，C是 $A B$ 上的一点， $A B = 5 cm ， A C = 4 cm$ ，将橡皮筋从C点向上垂直拉升2 $cm$ 到D点．

(1)、求 $A D$ 的长；

(2)、判断 $△ A B D$ 的形状，并说明理由．

查看试题解析
19. 如图，四边形纸片 $A B C D$ ， $A B ⊥ B C$ ．经测得 $A B = 9 cm$ ， $B C = 12 cm$ ， $C D = 8 cm$ ， $A D = 17 cm$ ．

(1)、求A、C两点之间的距离．

(2)、求这张纸片的面积．

查看试题解析
20. 如图，某港口 $P$ 位于东西方向的海岸线上，“远航”号、“海天”号轮船同时离开港口，各自沿一固定方向航行，“远航”号每小时航行 $16$ 海里，“海天”号每小时航行 $12$ 海里.它们离开港口一小时后分别位于点 $Q, R$ 处，且相距 $20$ 海里.如果知道“远航”号沿北偏东 $5 0^{°}$ 方向航行，你能判断“海天”号沿哪个方向航行吗?请说明理由.

查看试题解析