2025年山东省青岛市中考数学模拟试题
试卷日期:2025-03-19 考试类型:中考模拟
一、选择题(每题3分,共27分)
-
1. 港珠澳大桥东起香港国际机场附近的香港口岸人工岛,向西横跨伶仃洋海域后连接珠海和澳门人工岛,止于珠海港湾,全长55千米,设计时速100千米/小时,工程项目总投资额1269亿元,用科学记数法表示1269亿元为( )A、1269×108 B、1.269×108 C、1.269×1010 D、1.269×10112. 已知数a,b,c在数轴上的位置如图所示,化简|a + b| - |a - b| + |a + c|的结果为( )
 A、-a-c B、-a-b-c C、-a-2b-c D、a-2b+c3. 鲁班锁,民间也称作孔明锁、八卦锁,它起源于中国古代建筑中首创的榫卯结构.如图是鲁班锁的其中一个部件,从正面看到的平面图形是( )
A、-a-c B、-a-b-c C、-a-2b-c D、a-2b+c3. 鲁班锁,民间也称作孔明锁、八卦锁,它起源于中国古代建筑中首创的榫卯结构.如图是鲁班锁的其中一个部件,从正面看到的平面图形是( ) A、
A、 B、
B、 C、
C、 D、
D、 4. 如图,点 都在方格纸的格点上,若点A的坐标为 ,点B的坐标为 ,则点C的坐标是( )
4. 如图,点 都在方格纸的格点上,若点A的坐标为 ,点B的坐标为 ,则点C的坐标是( )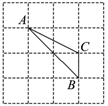 A、 B、 C、 D、5. 如图, , E为的中点,与相交于点F, , 则的度数是( )
A、 B、 C、 D、5. 如图, , E为的中点,与相交于点F, , 则的度数是( ) A、56° B、62° C、63° D、72°6. 如图,是的直径,C , D是上的两点,若 , 则的大小为( )
A、56° B、62° C、63° D、72°6. 如图,是的直径,C , D是上的两点,若 , 则的大小为( )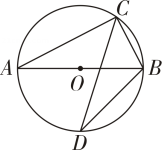 A、41° B、45° C、49° D、59°
A、41° B、45° C、49° D、59°二、填空题(每空3分,共18分)
三、作图题(共8分)
-
7. 如图, 在矩形中,是对角线.
 (1)、用尺规完成基本作图:作线段的垂直平分线,交于点O,交、延长线分别于点 E、F, 连接、 . (保留作图痕迹, 不写作法)(2)、求证: 四边形是菱形.
(1)、用尺规完成基本作图:作线段的垂直平分线,交于点O,交、延长线分别于点 E、F, 连接、 . (保留作图痕迹, 不写作法)(2)、求证: 四边形是菱形.四、解答题(共9题,共67分)
-
8. 阅读材料,并解决问题.
【学习研究】我国古代数学家赵爽在其所著的《勾股圆方图注》中记载了一元二次方程的几何解法,以为例,构造方法如下:

首先将方程变形为 , 然后画四个长为 , 宽为的矩形,按如图1所示的方式拼成一个“空心”大正方形,则图1中大正方形的面积可表示为 , 还可表示为四个矩形与一个边长为的小正方形面积之和,即 . 因此,可得新方程 . 因为表示边长,所以 , 即 . 遗憾的是,这样的做法只能得到方程的其中一个正根.
【理解应用】参照上述图的方法,请在下面三个构图中选择能够用几何法求解方程的正确构图是______.(从序号①②③中选择)

【类比迁移】小颖根据以上解法解方程 , 请将其解答过程补充完整:
第一步:将原方程变形为 , 即;
第二步:利用四个全等的矩形构造“空心”大正方形;
第三步:根据大正方形的面积可得新的方程______,解得原方程的一个根为______;
【拓展应用】一般地,对于形如的一元二次方程可以构造图2来解.

已知图2是由四个面积为3的相同矩形构成,中间围成的正方形面积为4,那么此方程的系数______,______,求得方程的正根为______.
9. 正方形的边长为5,E、F分别是边上的点,且 , 将绕点D逆时针旋转 , 得到 . (1)、求证:;(2)、若 , 求的长.
(1)、求证:;(2)、若 , 求的长.
-