人教版八年级上学期数学课时进阶测试15.2分式的运算（三阶）

试卷日期：2024-11-20 考试类型：同步测试

前去【出卷网】下载

一、选择题（每题3分）

1. 某商店有A、B两箱水果，A箱水果重量为 ${(a + 1)}^{2}$ 千克，B箱水果重量为 $(a^{2} - 1)$ 千克（其中 $a > 1$ ），两箱水果均卖了120元，那么A箱水果的单价是B箱水果单价的（）

A、 $\frac{a + 1}{a - 1}$ B、 $\frac{1}{a + 1}$ C、 $\frac{1}{a - 1}$ D、 $\frac{a - 1}{a + 1}$

查看试题解析
2. 已知：a，b，c三个数满足： $\frac{a b}{a + b} = \frac{1}{2}$ ， $\frac{b c}{b + c} = \frac{1}{3}$ ， $\frac{c a}{c + a} = \frac{1}{4}$ ，则 $\frac{a b c}{a b + b c + a c}$ 的值为（）

A、 $\frac{1}{9}$ B、 $\frac{2}{9}$ C、 $\frac{9}{2}$ D、 $\frac{1}{5}$

查看试题解析
3. 小明在纸上书写了一个正确的演算过程，同桌小亮一不小心撕坏了一角，如图所示，则撕坏的一角中“”为（）

A、 $\frac{1}{a - 4}$ B、 $\frac{4}{a + 1}$ C、 $\frac{1}{4 - a}$ D、 $- \frac{1}{a + 1}$

查看试题解析
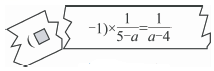4. 老师设计了接力游戏，甲、乙、丙、丁四位同学用合作的方式完成分式化简．规则是：每人只能看到前一人给的式子，并进行一步计算，再将结果传递给下一人，整个化简过程如图所示，接力中，自己负责的一步出现错误的同学是（）

A、甲和乙 B、乙和丙 C、丙和丁 D、甲和丁

查看试题解析
5. 对于下列说法，错误的个数是（　　）
① $\frac{2 x - y}{π}$ 是分式；②当x≠1时， $\frac{x^{2} - 1}{x - 1} = x + 1$ 成立；③当x=﹣3时，分式 $\frac{x + 3}{| x | - 3}$ 的值是零；④a $\div b \times \frac{1}{b} = a \div 1 = a$ ；⑤ $\frac{a}{x} + \frac{a}{y} = \frac{2 a}{x + y}$ ；⑥2﹣x $\cdot \frac{3}{2 - x} = 3$ ．

A、6个 B、5个 C、4个 D、3个

查看试题解析
6. 若 $2^{m} = 3$ ， $3 \times 2^{n - m} = 2$ ，则 $m^{0} + {(- 2021)}^{n} =$ （）

A、 $2021$ B、 $- 2020$ C、 $- 2021$ D、 $- 2022$

查看试题解析
7. 若a²+2a﹣1＝0，则 $\frac{a^{2}}{a - 2}$ （a﹣ $\frac{4}{a}$ ）的值是（）

A、﹣3 B、﹣1 C、1 D、3

查看试题解析
8. 已知 $x^{2} - 3 x + 1 = 0$ ，则 $x^{2} + x^{- 2} + 3$ 值为（）

A、10 B、9 C、12 D、3

查看试题解析

二、填空题（每题2分）

9. 若（t-3）^t-2=1，则t=.

查看试题解析
10. 已知 $a^{2} - a b + b^{2} = 0 (a \neq 0 ， b \neq 0)$ ，则式子 $\frac{b}{a} + \frac{a}{b}$ 的值等于

查看试题解析
11. 已知正实数x，y，z满足：xy+yz+zx≠1，且 $\frac{(x^{2} - 1) (y^{2} - 1)}{x y} + \frac{(y^{2} - 1) (z^{2} - 1)}{y z} + \frac{(z^{2} - 1) (x^{2} - 1)}{z x}$ =4.求 $\frac{1}{x y} + \frac{1}{y z} + \frac{1}{z x}$ 的值为.

查看试题解析
12. 一个容器装有1L水，按照如下要求把水倒出：第1次倒出 $\frac{1}{2} L$ 水，第2次倒出的水量是 $\frac{1}{2} L$ 的 $\frac{1}{3}$ ，第3次倒出的水量是 $\frac{1}{3} L$ 的 $\frac{1}{4}$ ，第4次倒出的水量是 $\frac{1}{4} L$ 的 $\frac{1}{5}$ ……，则第n次倒出后，倒出的水的总量为L．

查看试题解析
13. 已知 $x - 3 y = 0$ ，则 $\frac{2 x + y}{x^{2} - 2 x y + y^{2}} \cdot (x - y)$ 的值为．

查看试题解析

三、计算题（共6分）

14. 计算下列各式，并把结果化为只含有正整数次幂的形式：

(1)、a^-2b²·(-2a²b^-2)^-2÷(a^-4b²)；

(2)、 ${(\frac{a^{- 2}}{b^{3}})}^{3}$ ÷ ${(\frac{a^{- 2}}{b^{3}})}^{2}$ · ${(\frac{a^{- 2}}{b^{3}})}^{- 4}$ .

查看试题解析

四、解答题（共10分）

15. 在平面直角坐标系 $x O y$ 中，我们称横、纵坐标都是整数的点为“整点”，若坐标系内两个“整点” $A (p ， q) ， B (m ， n) (m \leq n)$ 满足关于x的多项式 $x^{2} + p x + q$ 能够因式分解为 $（ x + m ）（ x + n ）$ ，则称点B是点A的分解点，例如 $A (5 ， 4) ， B (1 ， 4)$ 满足 $x^{2} + 5 x + 4 = (x + 1) (x + 4)$ ，所以B是A的“分解点”．

(1)、在点 $A_{1} (3 ， 2) ， A_{2} (0 ， 5) ， A_{3} (- 3 ， 0) ， A_{4} (9 ， 0)$ 中，请找出不存在的“分解点”的点_______．

(2)、点 $P (a ， 1)$ 存在分解点，求代数式 $\frac{3 - a}{2 a - 4} \div (a + 2 - \frac{5}{a - 2})$ 的值．

(3)、在P，Q都在纵轴y轴上，（P在Q的上方），点M在横轴x轴上，且点P、Q、M都存在“分解点”，若 $△ P Q M$ 面积为5，请直接写出点M的坐标．

查看试题解析