高三数学一轮复习阶段题型检测
试卷日期:2024-11-06 考试类型:一轮复习
一、选择题
-
1. 已知 , “”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分又不必要条件2. 已知集合 , , 则( )A、 B、 C、 D、3. 已知向量满足 , 且 , 则在上的投影向量为( )A、 B、 C、 D、4. 已知:不等式的解集为 , 则是的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件5. 已知向量满足 , 且 . 则( ).A、 B、 C、 D、16. 设z=5+i , 则i(+z)=( )A、10i B、2i C、10 D、﹣27. 在复平面内,对应的点位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限
二、多项选择题
-
8. 已知复数 , , 则下列说法正确的有( )A、 B、 C、 D、在复平面内 , 对应的点关于虚轴对称9. 已知向量满足 , 设 , 则( )A、 B、在方向上的投影向量为 C、的最小值为 D、无最大值10. 下列说法正确的是( )A、向量在向量上的投影向量的坐标为 B、“”是“直线与直线平行”的充要条件 C、若正数a,b满足 , 且 , 则 D、已知为两个不同的平面,m,n是两条不同的直线,若 , 则11. 设 , 为不同的直线, , 为不同的平面,则下列结论中正确的是( )A、若 , , 则 B、若 , , 则 C、若 , , 则 D、若 , , , 则12. 如图,在棱长为2的正方体中,E是线段的中点,点M,N满足 , 其中 , 则( )
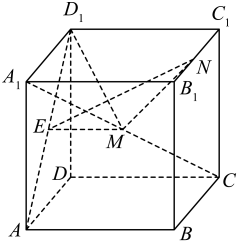 A、存在 , 使得 B、的最小值为 C、当时,直线与平面所成角的正弦值为 D、当时,过E,M,N三点的平面截正方体得到的截面多边形面积为13. 已知是定义在闭区间上的偶函数,且在y轴右侧的图象是函数图象的一部分(如图所示),则( )
A、存在 , 使得 B、的最小值为 C、当时,直线与平面所成角的正弦值为 D、当时,过E,M,N三点的平面截正方体得到的截面多边形面积为13. 已知是定义在闭区间上的偶函数,且在y轴右侧的图象是函数图象的一部分(如图所示),则( )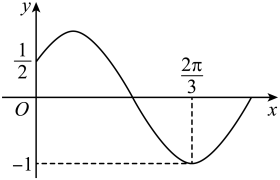 A、的定义域为 B、当时,取得最大值 C、当时,的单调递增区间为 D、当时,有且只有两个零点和14. 已知函数 , 下列说法正确的是( )A、的最小正周期为 B、点为图象的一个对称中心 C、若在上有两个实数根,则 D、若的导函数为 , 则函数的最大值为15. 下列命题中正确的有( )A、幂函数,且在单调递减,则 B、的单调递增区间是 C、定义域为 , 则 D、的值域是16. 若函数既有极大值也有极小值,则( ).A、 B、 C、 D、17. 关于函数 , 下列判断正确的是( )A、是的极大值点 B、函数有且只有1个零点 C、存在正实数 , 使得成立 D、对两个不相等的正实数 , , 若 , 则.18. 已知正数满足 , 则下列选项正确的是( )A、 B、 C、 D、19. 已知 , 是正数,且 , 下列叙述正确的是( )A、最大值为1 B、有最大值4 C、的最大值为2 D、的最小值为9
A、的定义域为 B、当时,取得最大值 C、当时,的单调递增区间为 D、当时,有且只有两个零点和14. 已知函数 , 下列说法正确的是( )A、的最小正周期为 B、点为图象的一个对称中心 C、若在上有两个实数根,则 D、若的导函数为 , 则函数的最大值为15. 下列命题中正确的有( )A、幂函数,且在单调递减,则 B、的单调递增区间是 C、定义域为 , 则 D、的值域是16. 若函数既有极大值也有极小值,则( ).A、 B、 C、 D、17. 关于函数 , 下列判断正确的是( )A、是的极大值点 B、函数有且只有1个零点 C、存在正实数 , 使得成立 D、对两个不相等的正实数 , , 若 , 则.18. 已知正数满足 , 则下列选项正确的是( )A、 B、 C、 D、19. 已知 , 是正数,且 , 下列叙述正确的是( )A、最大值为1 B、有最大值4 C、的最大值为2 D、的最小值为9三、解答题
-
20. 已知函数 .(1)、若 , 求的最大值;(2)、若 , 其中 , 求实数的取值范围.21. 已知函数f(x)=a(x﹣1)﹣lnx+1.(1)、求f(x)的单调区间;(2)、若a≤2时,证明:当x>1时,f(x)<ex﹣1恒成立.22. 已知函数f(x)=ln+ax+b(x﹣1)3 .(1)、若b=0,且f'(x)≥0,求a的最小值;(2)、证明:曲线y=f(x)是中心对称图形;(3)、若f(x)>﹣2当且仅当1<x<2,求b的取值范围.23. 已知椭圆椭圆的离心率.左顶点为 , 下顶点为B,C是线段OB的中点,其中.(1)、求椭圆方程.(2)、过点的动直线与椭圆有两个交点P,Q.在轴上是否存在点使得.若存在求出这个点纵坐标的取值范围,若不存在请说明理由.24. 双曲线 , , , 为左右顶点,过点的直线l交双曲线于两点P、Q , 且点P在第一象限.(1)、若时,求b.(2)、若 , 为等腰三角形时,求点的坐标.(3)、过点Q作OQ延长线交于点R , 若 , 求b取值范围.25. 已知圆经过点和 , 且圆心在直线上.(1)、求圆的方程;(2)、设直线经过点 , 且与圆相切,求直线的方程.(3)、为圆上任意一点,在(1)的条件下,求的最小值.26. 已知抛物线: .(1)、求抛物线的焦点F的坐标和准线的方程;(2)、过焦点F且斜率为的直线与抛物线交于两个不同的点A、B,求线段AB的长;(3)、已知点 , 是否存在定点Q,使得过点Q的直线与抛物线交于两个不同的点M、N(均不与点Р重合),且以线段MN为直径的圆恒过点P?若存在,求出点Q的坐标;若不存在,请说明理由.27. 已知圆C: .(1)、设点 , 过点M作直线l与圆C交于A , B两点,若 , 求直线l的方程;(2)、设P是直线上的点,过P点作圆C的切线PA , PB , 切点为A , B , 求证:经过A , P , C三点的圆必过定点,并求出所有定点的坐标.