湖南省娄底市新化县2017年中考数学二模试卷

试卷日期：2017-12-07 考试类型：中考模拟

前去【出卷网】下载

一、选择题

1. ﹣ $\frac{1}{2}$ 的相反数是（　　）

A、2 B、﹣2 C、 $\frac{1}{2}$ D、﹣ $\frac{1}{2}$

查看试题解析
2. 节约是一种美德，节约是一种智慧，据不完全统计，全国每年浪费的食物若折合成粮食可养活约360000000人，把350000000用科学记数法可以表示为（）

A、3.5×10¹⁰ B、3.5×10⁹ C、3.5×10⁸ D、3.5×10⁷

查看试题解析
3. 下列运算正确的是（　　）

A、x²•x³=x⁶ B、x⁶÷x⁵=x C、（﹣x²）⁴=x⁶ D、x²+x³=x⁵

查看试题解析
4. 下列说法正确的是（）

A、对角线互相垂直的四边形是菱形 B、矩形的对角线互相垂直 C、一组对边平行的四边形是平行四边形 D、四边相等的四边形是菱形

查看试题解析
5. 某校举行健美操比赛，甲、乙两班个班选20名学生参加比赛，两个班参赛学生的平均身高都是1.65米，其方差分别是s_甲²=1.9，s_乙²=2.4，则参赛学生身高比较整齐的班级是（）

A、甲班 B、乙班 C、同样整齐 D、无法确定

查看试题解析
6. 某几何体的三视图如图所示，则这个几何体是（）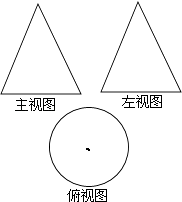

A、圆柱 B、正方体 C、球 D、圆锥

查看试题解析
7. 如图AB∥DE，∠ABC=30°，∠BCD=80°，则∠CDE=（）

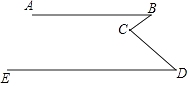A、20° B、50° C、60° D、100°

查看试题解析
8. 已知方程组 ${\begin{matrix} 2 x + y = 4 \\ x + 2 y = 5 \end{matrix}$ ，则x+y的值为（）

A、﹣1 B、0 C、2 D、3

查看试题解析
9. 如图，在△ABC中，AD，BE是两条中线，则S_△_EDC：S_△_ABC=（）

A、1：2 B、1：4 C、1：3 D、2：3

查看试题解析
10. 若一次函数y=（k﹣1）x+3的图象经过第一、二、四象限，则k的取值范围是（）

A、k＞0 B、k＜0 C、k＞1 D、k＜1

查看试题解析
11. 关于x的方程（a﹣5）x²﹣4x﹣1=0有实数根，则a满足（　　）

A、a≥1 B、a＞1且a≠5 C、a≥1且a≠5 D、a≠5

查看试题解析
12. 遂宁市某生态示范园，计划种植一批核桃，原计划总产量达36万千克，为了满足市场需求，现决定改良核桃品种，改良后平均每亩产量是原计划的1.5倍，总产量比原计划增加了9万千克，种植亩数减少了20亩，则原计划和改良后平均每亩产量各多少万千克？设原计划每亩平均产量x万千克，则改良后平均每亩产量为1.5x万千克，根据题意列方程为（）

A、 $\frac{36}{x}$ ﹣ $\frac{36 + 9}{1.5 x}$ =20 B、 $\frac{36}{x}$ ﹣ $\frac{36}{1.5 x}$ =20 C、 $\frac{36 + 9}{1.5 x}$ ﹣ $\frac{36}{x}$ =20 D、 $\frac{36}{x}$ + $\frac{36 + 9}{1.5 x}$ =20

查看试题解析

二、填空题

13. 若实数a、b满足|2017a﹣2018|+b²=0，则a^b的值为．

查看试题解析
14. 分式 $\frac{x^{2} - 9}{x + 3}$ 的值为0，那么x的值为．

查看试题解析
15. 如图是二次函数 $y_{1} = a x^{2} + b x + c$ 和一次函数y₂=kx+t的图象，当y₁≥y₂时，x的取值范围是．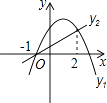

查看试题解析
16. 如图，⊙O的直径CD⊥EF，∠OEG=30°，则∠DCF=°．

查看试题解析
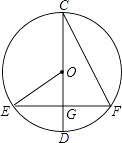17. 在10个外观相同的产品中，有3个不合格产品，现从中任意抽取1个进行检测，抽到合格产品的概率是．

查看试题解析
18. 已知：如图，O为坐标原点，四边形OABC为矩形，A（10，0），C（0，4），点D是OA的中点，点P在BC上运动，当△ODP是腰长为5的等腰三角形时，则P点的坐标为．

查看试题解析

三、解答题

19. 计算：|﹣2|+2^﹣¹﹣cos60°﹣（1﹣ $\sqrt{2}$ ）⁰ ．

查看试题解析
20. 已知a²﹣2a﹣2=0，求代数式（1﹣ $\frac{1}{a + 1}$ ）÷ $\frac{a^{3}}{a^{2} + 2 a + 1}$ 的值．

查看试题解析

四、解答题

21. 某市为了增强学生体质，全面实施“学生饮用奶”营养工程．某品牌牛奶供应商提供了原味、草莓味、菠萝味、香橙味、核桃味五种口味的牛奶提供学生饮用．浠马中学为了了解学生对不同口味牛奶的喜好，对全校订购牛奶的学生进行了随机调查（每盒各种口味牛奶的体积相同），绘制了如图两张不完整的人数统计图：

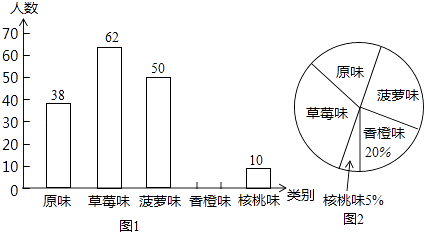(1)、本次被调查的学生有名；

(2)、补全上面的条形统计图1，并计算出喜好“菠萝味”牛奶的学生人数在扇形统计图中所占圆心角的度数；

(3)、该校共有1200名学生订购了该品牌的牛奶，牛奶供应商每天只为每名订购牛奶的学生配送一盒牛奶．要使学生每天都喝到自己喜好的口味的牛奶，牛奶供应商每天送往该校的牛奶中，草莓味要比原味多送多少盒？

查看试题解析
22. 如图，小俊在A处利用高为1.5米的测角仪AB测得楼EF顶部E的仰角为30°，然后前进12米到达C处，又测得楼顶E的仰角为60°，求楼EF的高度．（ $\sqrt{3}$ =1.732，结果精确到0.1米）

查看试题解析

五、解答题．

23. “汉十”高速铁路襄阳段正在建设中，甲、乙两个工程队计划参与一项工程建设，甲队单独施工30天完成该项工程的 $\frac{1}{3}$ ，这时乙队加入，两队还需同时施工15天，才能完成该项工程．

(1)、若乙队单独施工，需要多少天才能完成该项工程？

(2)、若甲队参与该项工程施工的时间不超过36天，则乙队至少施工多少天才能完成该项工程？

查看试题解析
24. 如图，E是▱ABCD的边CD的中点，延长AE交BC的延长线于点F.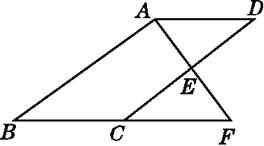

(1)、求证：△ADE≌△FCE.

(2)、若∠BAF=90°，BC=5，EF=3，求CD的长.

查看试题解析

六、解答题

25. 如图，AB是⊙O的直径，C、G是⊙O上两点，且AC=CG，过点C的直线CD⊥BG于点D，交BA的延长线于点E，连接BC，交OD于点F．

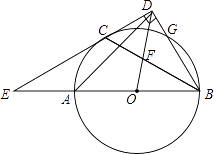(1)、求证：CD是⊙O的切线．

(2)、若 $\frac{O F}{F D} = \frac{2}{3}$ ，求∠E的度数．

(3)、连接AD，在（2）的条件下，若CD= $\sqrt{3}$ ，求AD的长．

查看试题解析
26. 如图，抛物线y=x²+bx+c与x轴交于A（﹣1，0），B（3，0）两点，顶点M关于x轴的对称点是M′．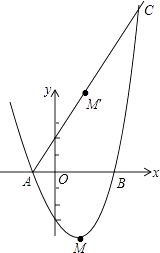

(1)、求抛物线的解析式；

(2)、若直线AM′与此抛物线的另一个交点为C，求△CAB的面积；

(3)、是否存在过A，B两点的抛物线，其顶点P关于x轴的对称点为Q，使得四边形APBQ为正方形？若存在，求出此抛物线的解析式；若不存在，请说明理由．

查看试题解析