上海市浦东新区2017-2018学年高三上学期数学期中考试试卷

试卷日期：2017-12-04 考试类型：期中考试

前去【出卷网】下载

一、填空题

1. 幂函数经过点 $(2 ， \frac{\sqrt{2}}{2})$ ，则此幂函数的解析式为．

查看试题解析
2. 若集合A={x|2x+1＞0}，B={x||x﹣1|＜2}，则A∩B= ．

查看试题解析
3. 设f^﹣¹（x）为f（x）= $\frac{x}{2 x + 1}$ 的反函数，则f^﹣¹（2）= ．

查看试题解析
4. 不等式 $\frac{1 - x}{x + 2} > 0$ 的解集是．

查看试题解析
5. 在一个圆周上有10个点，任取3个点作为顶点作三角形，一共可以作个三角形（用数字作答）．

查看试题解析
6. 已知球半径为2，球面上A、B两点的球面距离为 $\frac{2 π}{3}$ ，则线段AB的长度为．

查看试题解析
7. 已知x，y∈R⁺ ，且x+4y=1，则xy的最大值为．

查看试题解析
8. 在五个数字1，2，3，4，5中，若随机取出三个数字，则剩下两个数字都是奇数的概率是
（结果用数值表示）．

查看试题解析
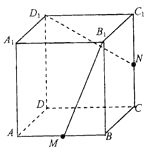
9. 若函数f（x）=（x+a）（bx+2a）（常数a、b∈R）是偶函数，且它的值域为（﹣∞，4]，则该函数的解析式f（x）= ．

查看试题解析
10. 已知总体的各个体的值由小到大依次为2，3，3，7，a，b，12，13.7，18.3，20，且总体的中位数为10.5，平均数为10．若要使该总体的方差最小，则a、b的取值分别是．

查看试题解析
11. 已知命题α：m²﹣4m+3≤0，命题β：m²﹣6m+8＜0．若α、β中有且只有一个是真命题，则实数m的取值范围是．

查看试题解析
12. 如图所示，在正方体ABCD﹣A₁B₁C₁D₁中，M、N分别是棱AB、CC₁的中点，△MB₁P的顶点P在棱CC₁与棱C₁D₁上运动，有以下四个命题：
①平面MB₁P⊥ND₁；②平面MB₁P⊥平面ND₁A₁；③△MB₁P在底面ABCD上的射影图形的面积为定值；④△MB₁P在侧面D₁C₁CD上的射影图形是三角形．
其中正确命题的序号是．

查看试题解析

二、选择题

13. 若关于x的一元二次方程ax²+bx+c=0有两个实数根，分别是x₁、x₂ ，则“ ${\begin{matrix} x_{1} + x_{2} > 2 \\ x_{1} x_{2} > 1 \end{matrix}$ ”是“两根均大于1”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要．

查看试题解析
14. 在下列命题中，不是公理的是（）

A、两条相交直线确定一个平面 B、不在同一条直线上的三点确定一个平面 C、如果直线上有两个点在平面α上，那么直线在平面α上 D、如果不同的两个平面α、β有一个公共点A，那么α、β的交集是过点A的直线．

查看试题解析
15. ${(x - \frac{1}{\sqrt[3]{x}})}^{12}$ 展开式中的常数项为（）

A、﹣1320 B、1320 C、﹣220 D、220

查看试题解析
16. 下列四个命题中正确是（）

A、函数y=a^x（a＞0且a≠1）与函数 $y = l o g_{a} a^{x}$ （a＞0且a≠1）的值域相同 B、函数y= $x^{3}$ 与y= $3^{x}$ 的值域相同 C、函数 $y = \frac{1}{2} + \frac{1}{2^{x} - 1}$ 与 $y = \frac{{(1 + 2^{x})}^{2}}{x \cdot 2^{x}}$ 都是奇函数 D、函数y= $(x - 1)^{2}$ 与y=2^x^﹣¹在区间[0，+∞）上都是增函数．

查看试题解析

三、解答题

17. 如图所示，圆锥SO的底面圆半径|OA|=1，其侧面展开图是一个圆心角为 $\frac{2 π}{3}$ 的扇形．

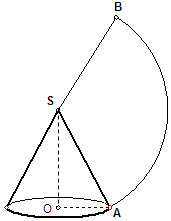(1)、求此圆锥的表面积；

(2)、求此圆锥的体积．

查看试题解析
18.

(1)、解方程：25^x⁺¹﹣9•5^x⁺²+500=0；

(2)、已知关于x的不等式ax²﹣5x+b＞0的解集为 $(- \frac{2}{3} ， \frac{1}{4})$ ，求关于x的不等式ax²+5x+b＜0的解集．

查看试题解析
19. 如图，正方体ABCD﹣A₁B₁C₁D₁的棱长为2，点P为面ADD₁A₁的对角线AD₁的中点．PM⊥平面ABCD交AD与M，MN⊥BD于N．

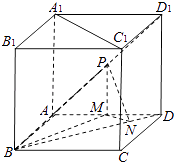(1)、求异面直线PN与A₁C₁所成角的大小；（结果可用反三角函数值表示）

(2)、求三棱锥P﹣BMN的体积．

查看试题解析
20. 已知函数 $f (x) = a^{x} + \frac{x - 2}{x + 1} (a > 1)$

(1)、判断函数f（x）的奇偶性，并说明理由；

(2)、证明：f（x）在（﹣1，+∞）上为增函数；

(3)、证明：方程f（x）=0没有负数根．

查看试题解析
21. 函数 f（x）=2x﹣ $\frac{a}{x}$ 的定义域为（0，1]（a为实数）．
（Ⅰ）当a=﹣1时，求函数y=f（x）的值域；
（Ⅱ）若函数y=f（x）在定义域上是减函数，求a的取值范围；
（Ⅲ）求函数y=f（x）在x∈（0，1]上的最大值及最小值，并求出函数取最值时x的值．

查看试题解析