2022年浙教版数学八下期末复习阶梯训练:特殊平行四边形(优生集训)
试卷日期:2022-04-15 考试类型:复习试卷
一、综合题
-
1. 如图1,在平面直角坐标系 中,已知四边形 的顶点 , 分别在 轴和 轴上.直线 经过点 ,与 轴交于点 .已知 , , . 平分 ,交 于点 ,点 是线段 上一动点.
 (1)、求 的长和 的度数;(2)、若点 是平面内任意一点,当以 、 、 、 为顶点的四边形为菱形时,求点 的坐标;(3)、如图2,在线段 上有一动点 ,点 与点 分别同时从点 和点 出发,已知当点 从点 匀速运动至点 时,点 恰好从点 匀速运动至点 ,连结 、 、 .问:在运动过程中,是否存在这样的点 和点 ,使得 的面积与 的面积相等.若存在,请直接写出相应的点 的坐标,若不存在,请说明理由.2. 如图1,在平面直角坐标系中,直线 与 轴交于点 ,与 轴交于点 与直线 交于点 ,直线 与 轴交于点 .
(1)、求 的长和 的度数;(2)、若点 是平面内任意一点,当以 、 、 、 为顶点的四边形为菱形时,求点 的坐标;(3)、如图2,在线段 上有一动点 ,点 与点 分别同时从点 和点 出发,已知当点 从点 匀速运动至点 时,点 恰好从点 匀速运动至点 ,连结 、 、 .问:在运动过程中,是否存在这样的点 和点 ,使得 的面积与 的面积相等.若存在,请直接写出相应的点 的坐标,若不存在,请说明理由.2. 如图1,在平面直角坐标系中,直线 与 轴交于点 ,与 轴交于点 与直线 交于点 ,直线 与 轴交于点 . (1)、求直线 的解析式;(2)、如图2,点 在线段 上,连接 ,过点 的直线交 轴负半轴于点 交 轴正半轴于点 ,请问: 是否为定值?若是,求出定值;若不是,请说明理由.(3)、 当点 在直线 上运动时,平面内是否存在一点 ,使得以点 为顶点的四边形是菱形?若存在,求出点 的坐标;若不存在,请说明理由.3. 如图,平行四边形ABCD中,AE⊥CD于E,BF平分∠ABC与AD交于F.AE与BF交于G.
(1)、求直线 的解析式;(2)、如图2,点 在线段 上,连接 ,过点 的直线交 轴负半轴于点 交 轴正半轴于点 ,请问: 是否为定值?若是,求出定值;若不是,请说明理由.(3)、 当点 在直线 上运动时,平面内是否存在一点 ,使得以点 为顶点的四边形是菱形?若存在,求出点 的坐标;若不存在,请说明理由.3. 如图,平行四边形ABCD中,AE⊥CD于E,BF平分∠ABC与AD交于F.AE与BF交于G.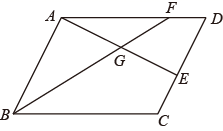 (1)、延长DC到H,使CH=DE,连接BH.求证:四边形ABHE是矩形.(2)、在(1)所画图形中,在CH的延长线上取HK=AG,当AE=AF时,求证:CK=AD.4. 如图1,在平面直角坐标系xOy中,直线l1:y=x+6交x轴于点A,交y轴于点B,经过点B的直线l2:y=kx+b交x轴于点C,且l2与l1关于y轴对称.
(1)、延长DC到H,使CH=DE,连接BH.求证:四边形ABHE是矩形.(2)、在(1)所画图形中,在CH的延长线上取HK=AG,当AE=AF时,求证:CK=AD.4. 如图1,在平面直角坐标系xOy中,直线l1:y=x+6交x轴于点A,交y轴于点B,经过点B的直线l2:y=kx+b交x轴于点C,且l2与l1关于y轴对称.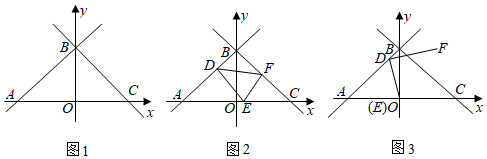 (1)、求直线l2的函数表达式;(2)、点D,E分别是线段AB,AC上的点,将线段DE绕点D逆时针α度后得到线段DF.
(1)、求直线l2的函数表达式;(2)、点D,E分别是线段AB,AC上的点,将线段DE绕点D逆时针α度后得到线段DF.①如图2,当点D的坐标为(﹣2,m),α=45°,且点F恰好落在线段BC上时,求线段AE的长;
②如图3,当点D的坐标为(﹣1,n),α=90°,且点E恰好和原点O重合时,在直线y=3﹣ 上是否存在一点G,使得∠DGF=∠DGO?若存在,直接写出点G的坐标;若不存在,请说明理由.
5. 已知点E是正方形ABCD的边CD上的动点,连接AE,过点A作AF⊥AE,交CB的延长线于点F. (1)、如图1,求证:FB=ED;(2)、点G为正方形ABCD的对角线BD上一点,连接AG,GC,GF,且GC=GF.
(1)、如图1,求证:FB=ED;(2)、点G为正方形ABCD的对角线BD上一点,连接AG,GC,GF,且GC=GF.①如图2,求∠GFA的度数;
②如图3,过点G作MH AE,分别交AF,AB,DC于点M,N,H.若AB=3,BF=1,求MH的长.
6. 如图,在平面直角坐标系中,四边形ABCO是矩形,已知点B坐标为(10,8),M,N分别是OC,AB的中点.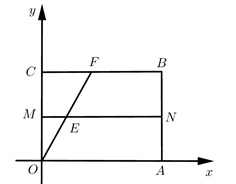 (1)、求证:四边形BCMN是矩形;(2)、点F是直线BC上一点,连接OF交直线MN于点E,当OF=OA时,求直线AF的解析式;(3)、在(2)的条件下,直线l经过点A,且解析式为y=kx+b(k≠0),若直线l与线段EM相交,求k的取值范围.7. 如图,在矩形ABCD中,O为对角线AC的中点,过点O作直线分别与矩形的边AD , BC交于M , N两点,连接CM , AN .
(1)、求证:四边形BCMN是矩形;(2)、点F是直线BC上一点,连接OF交直线MN于点E,当OF=OA时,求直线AF的解析式;(3)、在(2)的条件下,直线l经过点A,且解析式为y=kx+b(k≠0),若直线l与线段EM相交,求k的取值范围.7. 如图,在矩形ABCD中,O为对角线AC的中点,过点O作直线分别与矩形的边AD , BC交于M , N两点,连接CM , AN .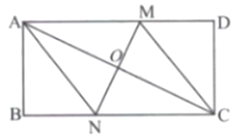 (1)、求证:四边形ANCM为平行四边形;(2)、若AD=4,AB=2,且MN⊥AC , 求DM的长.8. 阅读短文,解决问题
(1)、求证:四边形ANCM为平行四边形;(2)、若AD=4,AB=2,且MN⊥AC , 求DM的长.8. 阅读短文,解决问题定义:三角形的一个角与菱形的一个角重合,且菱形的这个角的对角顶点在三角形的这个角的对边上,则称这个菱形为该三角形的“亲密菱形”﹒例如:如图1,四边形 为菱形, 与 重合,点 在 上,则称菱形 为 的“亲密菱形”.
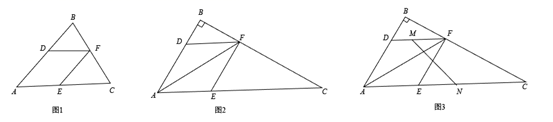
如图2,在 中, , 平分 ,交 于点 ,过点 作 , .
(1)、求证:四边形 为 的“亲密菱形”;(2)、若 , ,求四边形 的周长;(3)、如图3, 、 分别是 、 的中点,连接 .若 ,求 的值.9. 如图,矩形ABCD中,AD=2AB,E是AD边上一点,DE= AD(n为大于2的整数),连接BE,BE的垂直平分线分别交AD,BC于点F,G,FG与BE的交点为O,连接BF和EG。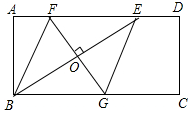 (1)、试判断四边形BFEG的形状,并说明理由;(2)、当AB=4,n=3时,求FG的长;(3)、记四边形BFEG的面积为S1 , 矩形ABCD的面积为S2 , 当 时,求n的值(直接写出结果,不必写出解答过程)。10. 如图,在平面直角坐标系中,直线l1:y=- +x+6分别与x轴、轴交于点B、C,且与直线l2:y= x交于A。
(1)、试判断四边形BFEG的形状,并说明理由;(2)、当AB=4,n=3时,求FG的长;(3)、记四边形BFEG的面积为S1 , 矩形ABCD的面积为S2 , 当 时,求n的值(直接写出结果,不必写出解答过程)。10. 如图,在平面直角坐标系中,直线l1:y=- +x+6分别与x轴、轴交于点B、C,且与直线l2:y= x交于A。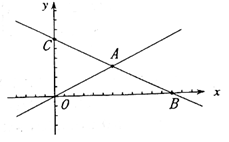 (1)、分别求出A、B、C的坐标;(2)、若D是线段OA上的点,且△COD的面积为l2 , 求直线CD的函数表达式;(3)、在(2)的条件下,设P是射线CD上的点,在平面内是否存在点Q,使以O、C、P、Q为顶点的四边形是菱形?若存在,直接写出点Q的坐标;若不存在,请说明理由。11. 如图1,直线 与y轴交于点 ,与x轴交于点 .
(1)、分别求出A、B、C的坐标;(2)、若D是线段OA上的点,且△COD的面积为l2 , 求直线CD的函数表达式;(3)、在(2)的条件下,设P是射线CD上的点,在平面内是否存在点Q,使以O、C、P、Q为顶点的四边形是菱形?若存在,直接写出点Q的坐标;若不存在,请说明理由。11. 如图1,直线 与y轴交于点 ,与x轴交于点 .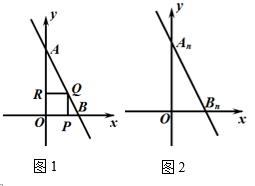 (1)、按题意填表:
(1)、按题意填表:n
1
2
3
4
5
0
0
0
0
0
4
2
0
0
0
0
0
(2)、由(1)中表格中的数据可以发现:①对于 , = , = , , ;
②直线 一定经过的点的坐标为;
(3)、如图2,正方形OPQR是△ 的内接正方形,设正方形的边长为m ,求证:1<m<2.
12. 在正方形ABCD中,点E,F,G分别在边AD,AB,CD上(点E、F、G不与正方形的顶点重合),BE,FG相交于点O,且FG⊥BE.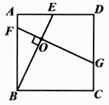 (1)、猜想BE与FG的数量关系并证明;(2)、证明:DG=AF+AE;(3)、若AE= ,FG=4,请直接写出点C到直线BE的距离;13. 如图,已知 ,直线 垂直平分 ,与边 交于点 ,连接 ,过点 作 交 于点 ,连接 .
(1)、猜想BE与FG的数量关系并证明;(2)、证明:DG=AF+AE;(3)、若AE= ,FG=4,请直接写出点C到直线BE的距离;13. 如图,已知 ,直线 垂直平分 ,与边 交于点 ,连接 ,过点 作 交 于点 ,连接 .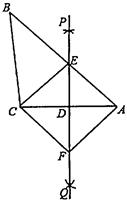 (1)、求证: ;(2)、求证:四边形 是菱形;(3)、若 , ,则菱形 的面积是多少?14. 如图,在正方形ABCD中,E是边AB上的点,连接CE,过点D作DF⊥CE,分别交BC、CE于点F、G
(1)、求证: ;(2)、求证:四边形 是菱形;(3)、若 , ,则菱形 的面积是多少?14. 如图,在正方形ABCD中,E是边AB上的点,连接CE,过点D作DF⊥CE,分别交BC、CE于点F、G (1)、求证:CE=DF;(2)、若AB=3,图中阴影部分的面积和与正方形ABCD的面积之比为2:3,则△DCG的面积为 , CG+DG的长为15. 如图,在矩形ABCD中,AB =2,E、F分别是边BC,AD上的点,连接EF,将四边形CEFD沿EF折叠,C、D的对应点分别为点G、H,EG交边AD于点M,延长HF交边BC于点N
(1)、求证:CE=DF;(2)、若AB=3,图中阴影部分的面积和与正方形ABCD的面积之比为2:3,则△DCG的面积为 , CG+DG的长为15. 如图,在矩形ABCD中,AB =2,E、F分别是边BC,AD上的点,连接EF,将四边形CEFD沿EF折叠,C、D的对应点分别为点G、H,EG交边AD于点M,延长HF交边BC于点N (1)、求证:四边形EMFN是菱形;(2)、若FN⊥BC,直接写出四边形EMFN的一条对角线的长;(3)、若EF=MF,求EN的长16. 如图①,四边形ABCD是正方形,E是对角线BD上一点,连接AE、CE
(1)、求证:四边形EMFN是菱形;(2)、若FN⊥BC,直接写出四边形EMFN的一条对角线的长;(3)、若EF=MF,求EN的长16. 如图①,四边形ABCD是正方形,E是对角线BD上一点,连接AE、CE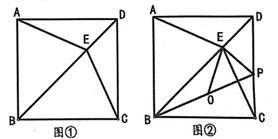 (1)、求证:AE=CE;(2)、如图②,点P是边CD上的一点,且PE⊥BD于E,连接BP,点O为BP的中点,连接OE。若∠PBC=30°,求∠POE的度数;(3)、在(2)的条件下,若OE= ,求CE的长。17. 如图所示,在中, , 点D从点C出发沿方向以每秒2个单位长度的速度向点A匀速运动,同时点E从点A出发沿方向以每秒1个单位长度的速度向点B匀速运动,当其中一个点达到终点时,另一个点也随之停止运动.设点运动的时间为t秒().过点作于点F,连接 .
(1)、求证:AE=CE;(2)、如图②,点P是边CD上的一点,且PE⊥BD于E,连接BP,点O为BP的中点,连接OE。若∠PBC=30°,求∠POE的度数;(3)、在(2)的条件下,若OE= ,求CE的长。17. 如图所示,在中, , 点D从点C出发沿方向以每秒2个单位长度的速度向点A匀速运动,同时点E从点A出发沿方向以每秒1个单位长度的速度向点B匀速运动,当其中一个点达到终点时,另一个点也随之停止运动.设点运动的时间为t秒().过点作于点F,连接 . (1)、求证:;(2)、四边形可能成为菱形吗?如果可能,求出相应的t值;如果不可能,说明理由.18. 如图:在平行四边形 中,点E在边 上,连接BE、 , 若 平分 , 平分 , 点G是 边的中点.
(1)、求证:;(2)、四边形可能成为菱形吗?如果可能,求出相应的t值;如果不可能,说明理由.18. 如图:在平行四边形 中,点E在边 上,连接BE、 , 若 平分 , 平分 , 点G是 边的中点.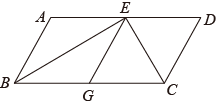 (1)、求 的度数.(2)、若 , , 求 的周长.(3)、判断四边形 的形状并证明.19. 如图,在▱ABCD 中,对角线 AC 与 BD 相交于点 O ,点 E , F 分别为 OB , OD 的中点,延长 AE 至 G ,使 EG =AE ,连接 CG .
(1)、求 的度数.(2)、若 , , 求 的周长.(3)、判断四边形 的形状并证明.19. 如图,在▱ABCD 中,对角线 AC 与 BD 相交于点 O ,点 E , F 分别为 OB , OD 的中点,延长 AE 至 G ,使 EG =AE ,连接 CG .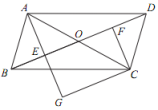 (1)、求证: △ABE≌△CDF ;(2)、当 AB 与 AC 满足什么数量关系时,四边形 EGCF 是矩形?请说明理由.20. 如图,在菱形ABCD中,AE⊥BC于点E.
(1)、求证: △ABE≌△CDF ;(2)、当 AB 与 AC 满足什么数量关系时,四边形 EGCF 是矩形?请说明理由.20. 如图,在菱形ABCD中,AE⊥BC于点E. (1)、如图1,若∠BAE=30°,AE=3,求菱形ABCD的周长及面积;(2)、如图2,作AF⊥CD于点F,连接EF,BD,求证:EF∥BD;(3)、如图3,设AE与对角线BD相交于点G,若CE=4,BE=8,四边形CDGE和△AGD的面积分别是S1和S2 , 求S1﹣S2的值.21. 如图,四边形ABCD为菱形,P为对角线BD上一点,连接AP并延长交射线BC于点E,连接PC.
(1)、如图1,若∠BAE=30°,AE=3,求菱形ABCD的周长及面积;(2)、如图2,作AF⊥CD于点F,连接EF,BD,求证:EF∥BD;(3)、如图3,设AE与对角线BD相交于点G,若CE=4,BE=8,四边形CDGE和△AGD的面积分别是S1和S2 , 求S1﹣S2的值.21. 如图,四边形ABCD为菱形,P为对角线BD上一点,连接AP并延长交射线BC于点E,连接PC.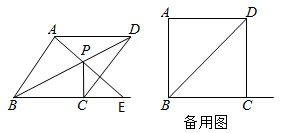 (1)、求证:∠AEB=∠PCD;(2)、当PA=PD且PC⊥BE时,求∠ABC的度数;(3)、若∠ABC=90°,△PCE是等腰三角形.直接写出∠PEC的度数 .22. 如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于F,以EC、CF为邻边作平行四边形ECFG,如图1所示.
(1)、求证:∠AEB=∠PCD;(2)、当PA=PD且PC⊥BE时,求∠ABC的度数;(3)、若∠ABC=90°,△PCE是等腰三角形.直接写出∠PEC的度数 .22. 如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于F,以EC、CF为邻边作平行四边形ECFG,如图1所示.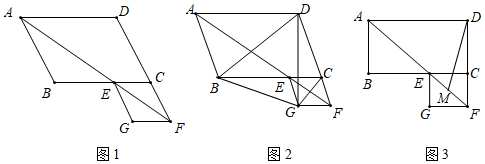 (1)、证明平行四边形ECFG是菱形;(2)、若∠ABC=120°,连接BG、CG、DG,如图2所示,
(1)、证明平行四边形ECFG是菱形;(2)、若∠ABC=120°,连接BG、CG、DG,如图2所示,①求证:△DGC≌△BGE;
②求∠BDG的度数;
(3)、若∠ABC=90°,AB=8,AD=14,M是EF的中点,如图3所示,求DM的长.23. 如图所示的是与菱形有关的三个图形.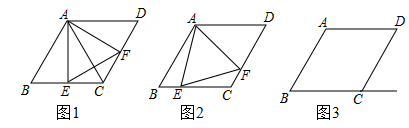 (1)、如图1,AC是菱形ABCD的对角线,∠B=60°,E、F分别是边BC、CD上的中点,连接AE、EF、AF.若AC=3,则CE+CF的长为 .(2)、如图2,在菱形ABCD中,∠B=60°.E是边BC上的点,连接AE,作∠EAF=60°,边AF交边CD于点F,连接EF.若BC=3,求CE+CF的长.(3)、在菱形ABCD中,∠B=60°,E是边BC延长线上的点,连接AE,作∠EAF=60°,边AF交边CD的延长线于点F,连接EF.当BC=3,EF⊥BC时,在图3中,将图形补充完整并求△AEF的周长.24. 如图,在 中, , 过点 的直线MN//AB,为 边上一点,过点 作 , 垂足为点 , 交直线 于点 , 连接 , .
(1)、如图1,AC是菱形ABCD的对角线,∠B=60°,E、F分别是边BC、CD上的中点,连接AE、EF、AF.若AC=3,则CE+CF的长为 .(2)、如图2,在菱形ABCD中,∠B=60°.E是边BC上的点,连接AE,作∠EAF=60°,边AF交边CD于点F,连接EF.若BC=3,求CE+CF的长.(3)、在菱形ABCD中,∠B=60°,E是边BC延长线上的点,连接AE,作∠EAF=60°,边AF交边CD的延长线于点F,连接EF.当BC=3,EF⊥BC时,在图3中,将图形补充完整并求△AEF的周长.24. 如图,在 中, , 过点 的直线MN//AB,为 边上一点,过点 作 , 垂足为点 , 交直线 于点 , 连接 , . (1)、求证:;(2)、当为中点时,四边形 是什么特殊四边形?说明你的理由;(3)、在()的条件下,当 的大小满足什么条件时,四边形 是正方形?请说明你的理由.25. 请认真完成下列数学活动
(1)、求证:;(2)、当为中点时,四边形 是什么特殊四边形?说明你的理由;(3)、在()的条件下,当 的大小满足什么条件时,四边形 是正方形?请说明你的理由.25. 请认真完成下列数学活动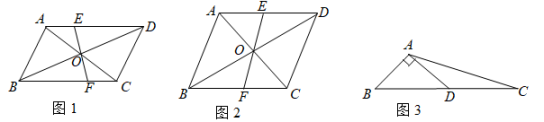
典例再现:如图1,▱ABCD的对线AC,BD相交于点O,EF过点O且与AD,BC分别相交于点E,F.求证:OE=OF.
(1)、尝试发现按图1填空:
①若▱ABCD的周长是24,OE=2,则四边形ABFE的周长为;
②若▱ABCD的面积是20,则四边形ABFE的面积是 .
(2)、应用发现如图2,在菱形ABCD中,对角线相交于点O,过点O的直线分别交AD,BC于点E,F.若AC= , AD=6,求四边形ABFE的面积.
(3)、应用拓展如图3,在△ABC中,点D是BC的中点,连接AD,若∠BAD=90°,AB=2,AC= , 则△ABC的面积是 .
26. 某数学兴趣小组在课外活动中,研究三角形和正方形的性质时,做了如下探究:在 中, , ,点 为直线 上一动点(点 不与 , 重合),以 为边在 右侧作正方形 ,连接 .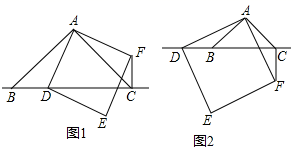 (1)、观察猜想
(1)、观察猜想如图1,当点 在线段 上时,
① 与 的位置关系为: ▲ ;
② , , 之间的数量关系为: ▲ ;
请将结论直接写在横线上,并给予证明;
(2)、数学思考如图2,当点 在线段 的延长线上时,(1)中的①,②结论是否仍然成立?若成立,请给予证明;若不成立,请你写出符合题意结论再给予证明.