2022年浙教版数学八下期末复习阶梯训练:反比例函数(优生集训)
试卷日期:2022-04-04 考试类型:复习试卷
一、综合题
-
1. 在平面直角坐标系中,四边形ABCD是平行四边形,且A(﹣1,0),B(0,﹣ ),C(3,0).
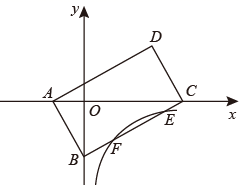 (1)、求证:四边形ABCD是矩形;(2)、若反比例函数y= 的图象与线段BC交于点E,F,且BF=EF.
(1)、求证:四边形ABCD是矩形;(2)、若反比例函数y= 的图象与线段BC交于点E,F,且BF=EF.①求点F的横坐标;
②求k值.
2. 如图,直线 与反比例函数 交于点 ,与 轴交于点 ,连接 , .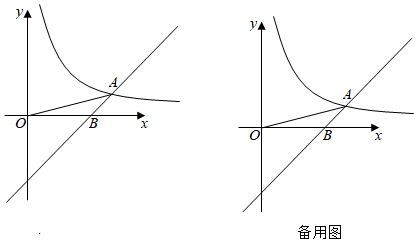 (1)、求点 的坐标及 的值;(2)、过 轴正半轴上一点 作 轴的垂线与直线 与反比例函数 的图象分别交于点 、 两点.
(1)、求点 的坐标及 的值;(2)、过 轴正半轴上一点 作 轴的垂线与直线 与反比例函数 的图象分别交于点 、 两点.①当 时,求 的长;
②若以 、 、 、 为顶点的四边形为平行四边形,求 的值;
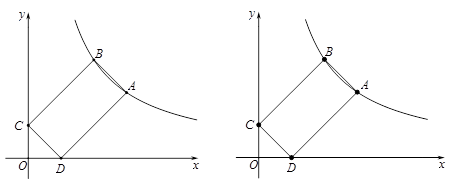
(3)、直线 与直线 、反比例函数 的图象分别交于 、 ,若 ,直接写出 的取值范围.3. 如图,在平面直角坐标系中,过点M (0,2)的直线l与x轴平行,且直线l分别与反比例函数y= (x> 0)和y= (x< 0)的图象交于点P,点Q。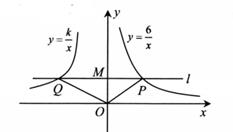 (1)、求点P的坐标;(2)、若△POQ的面积为7,求k的值。4. 点 为平面直角坐标系的原点,点 、 在反比例函数 的图象上,点 、 在反比例函数 的图象上,且 .
(1)、求点P的坐标;(2)、若△POQ的面积为7,求k的值。4. 点 为平面直角坐标系的原点,点 、 在反比例函数 的图象上,点 、 在反比例函数 的图象上,且 . (1)、若点 的坐标为 ,点 恰好为 的中点,过点 作 轴于点 ,交 的图象于点 .
(1)、若点 的坐标为 ,点 恰好为 的中点,过点 作 轴于点 ,交 的图象于点 .①请求出 、 的值;
②试求 的面积.
(2)、若 轴, , 与 间的距离为6,试说明 的值是否为某一固定值?如果是定值,试求出这个定值;若不是定值,请说明理由.5. 如图,在平面直角坐标系中,直线y=-x+5与反比例函数y= (x>0)的图象相交于点A(3,a)和点B(b , 3),点D , C分别是x轴和y轴的正半轴上的动点,且满足CD∥AB.
 (1)、求a , b的值及反比例函数的解析式;(2)、若OD=1,求点C的坐标,判断四边形ABCD的形状并说明理由;(3)、若点M是反比例函数y= (x>0)图象上的一个动点,当△AMD是以AM为直角边的等腰直角三角形时,求点M的坐标.6. 已知一次函数y=kx+b与反比例函数 的图象交于A(﹣3,2)、B(1,n)两点.
(1)、求a , b的值及反比例函数的解析式;(2)、若OD=1,求点C的坐标,判断四边形ABCD的形状并说明理由;(3)、若点M是反比例函数y= (x>0)图象上的一个动点,当△AMD是以AM为直角边的等腰直角三角形时,求点M的坐标.6. 已知一次函数y=kx+b与反比例函数 的图象交于A(﹣3,2)、B(1,n)两点.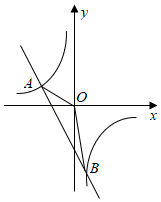 (1)、求一次函数和反比例函数的表达式;(2)、求△AOB的面积;(3)、直接写出不等式 的解集.(4)、点P在x轴上,当△PAO为等腰三角形时,直接写出点P的坐标.7. 已知:如图,平面直角坐标系中有一个等腰梯形 ,且 ,点 在 轴正半轴上,点 在 轴上(点 在点 的左侧),点 在第一象限, ,梯形的高为 .双曲线 经过点 ,直线 经过 两点.
(1)、求一次函数和反比例函数的表达式;(2)、求△AOB的面积;(3)、直接写出不等式 的解集.(4)、点P在x轴上,当△PAO为等腰三角形时,直接写出点P的坐标.7. 已知:如图,平面直角坐标系中有一个等腰梯形 ,且 ,点 在 轴正半轴上,点 在 轴上(点 在点 的左侧),点 在第一象限, ,梯形的高为 .双曲线 经过点 ,直线 经过 两点.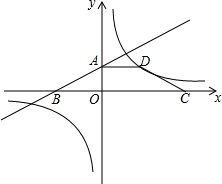 (1)、求双曲线 和直线 的解析式;(2)、点 在双曲线上,点 在 轴上,如果四边形 是平行四边形,请直接写出点 的坐标.8. 如图,已知反比例函数的图象与直线相交于点 , .
(1)、求双曲线 和直线 的解析式;(2)、点 在双曲线上,点 在 轴上,如果四边形 是平行四边形,请直接写出点 的坐标.8. 如图,已知反比例函数的图象与直线相交于点 , .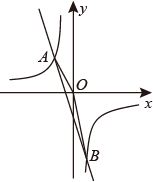 (1)、当x在什么范围内时,(直接写出答案)(2)、连接、 , 求的面积.9. 如图,在平面直角坐标系中,一次函数 的图像与反比例函数 ( >0)的图像相交于点A,一次函数 与x轴相交于点B ,与 轴相交于点C .
(1)、当x在什么范围内时,(直接写出答案)(2)、连接、 , 求的面积.9. 如图,在平面直角坐标系中,一次函数 的图像与反比例函数 ( >0)的图像相交于点A,一次函数 与x轴相交于点B ,与 轴相交于点C .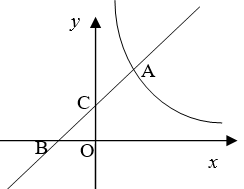 (1)、求 和 的值;(2)、点M在 轴正半轴上,且△ACM的面积为1 ,求点M坐标;(3)、在(2)的条件下,点P是一次函数 上一点,点Q是反比例函数 ( >0)图像上一点,且点P、 Q都在 轴上方。如果以B、M、P、Q为顶点的四边形为平行四边形,请直接写出点P、 Q的坐标.10. 如图6,正比例函数 的图象与反比例函数 的图象交于A、B两点,过点A
(1)、求 和 的值;(2)、点M在 轴正半轴上,且△ACM的面积为1 ,求点M坐标;(3)、在(2)的条件下,点P是一次函数 上一点,点Q是反比例函数 ( >0)图像上一点,且点P、 Q都在 轴上方。如果以B、M、P、Q为顶点的四边形为平行四边形,请直接写出点P、 Q的坐标.10. 如图6,正比例函数 的图象与反比例函数 的图象交于A、B两点,过点A作AC⊥x轴于点C , 连接BC , 若△ABC面积为2.
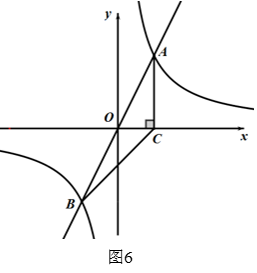 (1)、求k的值;(2)、在x轴上是否存在点D , 使△ABD为直角三角形?若存在,求出点D的坐标;若不存在,请说明理由.11. 如图,已知矩形OABC的两边OA,OC分别在x轴,y轴的正半轴上,且点B(4,3),反比例函数 图象与BC交于点D,与AB交于点E,其中D(1,3).
(1)、求k的值;(2)、在x轴上是否存在点D , 使△ABD为直角三角形?若存在,求出点D的坐标;若不存在,请说明理由.11. 如图,已知矩形OABC的两边OA,OC分别在x轴,y轴的正半轴上,且点B(4,3),反比例函数 图象与BC交于点D,与AB交于点E,其中D(1,3).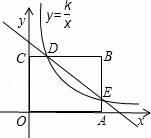 (1)、求反比例函数的解析式及E点的坐标;(2)、求直线DE的解析式;(3)、若矩形OABC对角线的交点为F(2, ),作FG⊥x轴交直线DE于点G.
(1)、求反比例函数的解析式及E点的坐标;(2)、求直线DE的解析式;(3)、若矩形OABC对角线的交点为F(2, ),作FG⊥x轴交直线DE于点G.①请判断点F是否在此反比例函数 的图象上,并说明理由;
②求FG的长度.
12. 已知 , 与 成正比例, 与 成反比例,当 时, ;当 时, .(1)、求 与 之间的函数关系式;(2)、当 时,求 的值.13. 已知:点 在反比例函数 的图像上,正比例函数的图象经过点 和点 .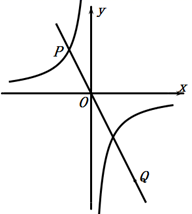 (1)、求点 的坐标;(2)、求正比例函数的解析式和点 的坐标;(3)、在 轴上求一点 ,使 的面积等于 .14. 如图所示,一次函数y=kx+b的图象与反比例函数y 交于A(1,t+2),B(﹣2t,﹣1)两点.
(1)、求点 的坐标;(2)、求正比例函数的解析式和点 的坐标;(3)、在 轴上求一点 ,使 的面积等于 .14. 如图所示,一次函数y=kx+b的图象与反比例函数y 交于A(1,t+2),B(﹣2t,﹣1)两点.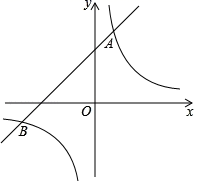 (1)、求一次函数和反比例函数的函数表达式;(2)、点C(x1 , y1)和D(x2 , y2)是反比例函数y 图象上任意两点,
(1)、求一次函数和反比例函数的函数表达式;(2)、点C(x1 , y1)和D(x2 , y2)是反比例函数y 图象上任意两点,①若x1<x2<0,p ,q ,试判断p、q的大小关系,并说明理由;
②若x1<﹣4,0<x2<1,过C、D两点分别作直线AB的垂线,垂足分别为E、F,当x1x2=﹣4时,判断四边形CEFD的形状,并说明理由.
15. 小明在研究矩形面积S与矩形的边长x,y之间的关系时,得到下表数据:x
0.5
1
1.5
2
3
4
6
12
y
12
6
4
3
2

1
0.5
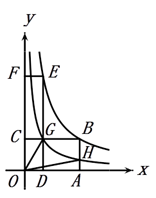
结果发现一个数据被墨水涂黑了.
(1)、被墨水涂黑的数据为.(2)、y与x之间的函数关系式为(其中x>0),且y随x的增大而.(3)、如图是小明画出的y关于x的函数图象,点B、E均在该函数的图象上,其中矩形OABC的面积记为S1 , 矩形ODEF的面积记为S2 , 请判断S1和S2的大小关系,并说明理由.(4)、在(3)的条件下,DE交BC于点G,反比例函数y= 的图象经过点G交AB于点H,连接OG、OH,则四边形OGBH的面积为.16. 某一农家计划利用已有的一堵长为8m的墙,用篱笆圈成一个面积为12m2的矩形ABCD花园,现在可用的篱笆总长为11m.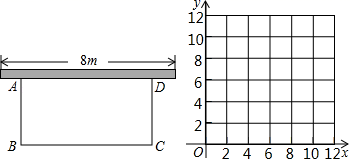 (1)、若设 , .请写出y关于x的函数表达式;(2)、若要使11m的篱笆全部用完,能否围成面积为15m2的花园?若能,请求出长和宽;若不能,请说明理由;(3)、若要使11m的篱笆全部用完,请写出y关于x的第二种函数解析式.请在坐标系中画出两个函数的图象,观察图象,满足条件的围法有几种?请说明理由.17. 如图,已知,A(0,4),B(﹣3,0),C(2,0),D为B点关于AC的对称点,反比例函数y= 的图象经过D点.
(1)、若设 , .请写出y关于x的函数表达式;(2)、若要使11m的篱笆全部用完,能否围成面积为15m2的花园?若能,请求出长和宽;若不能,请说明理由;(3)、若要使11m的篱笆全部用完,请写出y关于x的第二种函数解析式.请在坐标系中画出两个函数的图象,观察图象,满足条件的围法有几种?请说明理由.17. 如图,已知,A(0,4),B(﹣3,0),C(2,0),D为B点关于AC的对称点,反比例函数y= 的图象经过D点.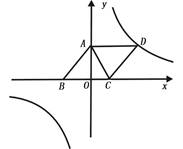 (1)、证明:四边形ABCD为菱形;(2)、求此反比例函数的解析式;(3)、设过点C和点D的一次函数y=kx+b,求不等式kx+b﹣ >0的解.(请直接写出当 时的答案);(4)、已知在y= 的图象上一点N,y轴上一点M,且点A、B、M、N组成四边形是平行四边形,求M点的坐标.18. 如图,一次函数 的图象与 轴交于点A,正方形ABCD的顶点B在 轴上,点D在直线 上,且AO=OB,反比例函数 ( )经过点C.
(1)、证明:四边形ABCD为菱形;(2)、求此反比例函数的解析式;(3)、设过点C和点D的一次函数y=kx+b,求不等式kx+b﹣ >0的解.(请直接写出当 时的答案);(4)、已知在y= 的图象上一点N,y轴上一点M,且点A、B、M、N组成四边形是平行四边形,求M点的坐标.18. 如图,一次函数 的图象与 轴交于点A,正方形ABCD的顶点B在 轴上,点D在直线 上,且AO=OB,反比例函数 ( )经过点C. (1)、求一次函数和反比例函数的解析式;(2)、点P是 轴上一动点,当 的周长最小时,求出P点的坐标;(3)、在(2)的条件下,以点C、D、P为顶点作平行四边形,直接写出第四个顶点M的坐标.19. 如图,在直角坐标系中,等腰三角形OAB的顶点A在反比例函数y 的图象上.若OA=AB=5,点B的坐标为(6,0).
(1)、求一次函数和反比例函数的解析式;(2)、点P是 轴上一动点,当 的周长最小时,求出P点的坐标;(3)、在(2)的条件下,以点C、D、P为顶点作平行四边形,直接写出第四个顶点M的坐标.19. 如图,在直角坐标系中,等腰三角形OAB的顶点A在反比例函数y 的图象上.若OA=AB=5,点B的坐标为(6,0).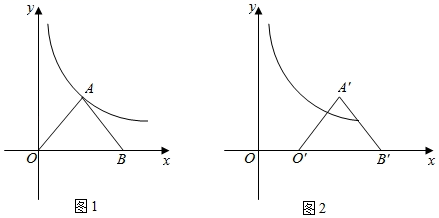 (1)、如图1,求反比例函数y 的表达式.(2)、如图2,把△OAB向右平移a个单位长度,对应得到△O'A'B',设A'B'的中点为M.
(1)、如图1,求反比例函数y 的表达式.(2)、如图2,把△OAB向右平移a个单位长度,对应得到△O'A'B',设A'B'的中点为M.①求点M的坐标(用含a的代数式表示);
②当反比例函数y 的图象经过点M时,求a的值.
20. 如图1,在平行四边形ABCD中,AD x轴,AD=7,原点O是对角线AC的中点,顶点A的坐标为(﹣3,3),反比例函数 在第一象限的图象过四边形ABCD的顶点D.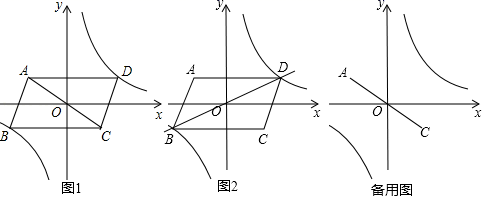 (1)、D点坐标为 , k=.(2)、①平行四边形ABCD的顶点B是否在反比例函数的图象上?为什么?
(1)、D点坐标为 , k=.(2)、①平行四边形ABCD的顶点B是否在反比例函数的图象上?为什么?②如图2,连接BD并延长,设直线BD解析式为 ,根据图象直接写出不等式 的x的取值范围;
(3)、是否存在两点P、Q分别在反比例函数图象的两支上,使得四边形AQCP是菱形?若存在,求出P、Q两点的坐标.21. 如图,反比例函数 (k>0)的图象与正比例函数 的图象交于A、B两点(点A在第一象限).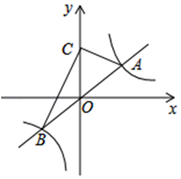 (1)、当点A的横坐标为2时.求k的值;(2)、若k=12,点C为y轴正半轴上一点,∠ACB=90°
(1)、当点A的横坐标为2时.求k的值;(2)、若k=12,点C为y轴正半轴上一点,∠ACB=90°①求 ACB的面积;
②以A、B、C、D为顶点作平行四边形,直接写出第四个顶点D的坐标.
22. 如图,在平面直角坐标系 中,函数 的图象经过点(-6,1),直线 与y轴交于点(0,-2).
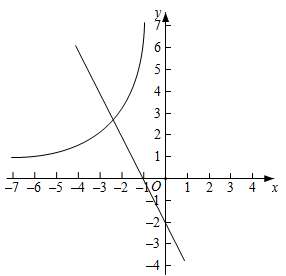 (1)、求k,m的值;(2)、过第二象限的点P(n,-2n)作平行于x轴的直线,交直线y=mx+m于点A,交函数 的图象于点B.
(1)、求k,m的值;(2)、过第二象限的点P(n,-2n)作平行于x轴的直线,交直线y=mx+m于点A,交函数 的图象于点B.①当n=-1时,判断线段PA与PB的数量关系,并说明理由;
②若PB≥2PA,结合函数的图象,直接写出n的取值范围.
23. 如图1,矩形的边OA在x轴上,边OC在y轴上,函数 (k>0,x>0)的图象与BC边相交于点M(点M不与点B、C重合),与AB边相交于点N, . (1)、若点B的坐标为(4,2),i=0.5,求k的值和点N的坐标;(2)、连接OB,过M作MQ⊥OB,垂足为Q;
(1)、若点B的坐标为(4,2),i=0.5,求k的值和点N的坐标;(2)、连接OB,过M作MQ⊥OB,垂足为Q;①如图2.当k=1, 时,设OB长为p,MQ长为q,求p与q的函数关系式;
②如图3,连接NQ,记四边形OANQ,△NQB,△QBM,四边形MCOQ的面积分别为S1、S2、S3、S4.判断S1+S3与S2+S4的数量关系,并说明理由.
24. 如图在平面直角坐标系中,O为原点,A、B两点分别在y轴、x轴的正半轴上,△AOB的一条内角平分线、一条外角平分线交于点P,P在反比例函数 的图像上. (1)、求点P的坐标;(2)、若OA=OB,则①∠P的度数为 ▲ ;②求出此时直线AB的函数关系式;(3)、如果直线AB的关系式为y=kx+n,且0<n<2,作反比例函数 ,过点P(0,1)作x轴的平行线与 的图像交于点M,与 的图像交于点N,过点N作y轴的平行线与y=kx+n的图像交于点Q,若MN+QN的和始终是一个定值d,求此时k的值及定值d.25. 如图,函数 的图象过点 和 两点
(1)、求点P的坐标;(2)、若OA=OB,则①∠P的度数为 ▲ ;②求出此时直线AB的函数关系式;(3)、如果直线AB的关系式为y=kx+n,且0<n<2,作反比例函数 ,过点P(0,1)作x轴的平行线与 的图像交于点M,与 的图像交于点N,过点N作y轴的平行线与y=kx+n的图像交于点Q,若MN+QN的和始终是一个定值d,求此时k的值及定值d.25. 如图,函数 的图象过点 和 两点 (1)、求n和k的值;(2)、将直线 沿x轴向左移动得直线 ,交x轴于点D,交y轴于点E,交 于点C,若 ,求直线 的解析式;(3)、在(2)的条件下,第二象限内是否存在点F,使得 为等腰直角三角形,若存在,请直接写出点F的坐标;若不存在,请说明理由.
(1)、求n和k的值;(2)、将直线 沿x轴向左移动得直线 ,交x轴于点D,交y轴于点E,交 于点C,若 ,求直线 的解析式;(3)、在(2)的条件下,第二象限内是否存在点F,使得 为等腰直角三角形,若存在,请直接写出点F的坐标;若不存在,请说明理由.