2022年浙教版数学八下期末复习阶梯训练:反比例函数(提高训练)
试卷日期:2022-04-04 考试类型:复习试卷
一、单选题
-
1. 函数 与 在同一平面直角坐标系中的图象可能是( )A、
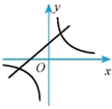 B、
B、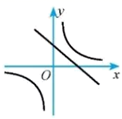 C、
C、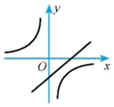 D、
D、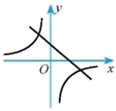 2. 关于反比例函数 的图象,下列说法正确的是( )A、 随着 的增大而增大 B、图象分布在一三象限 C、当 时, D、若 在该图象上,则 也在该图象上3. 已知函数 ,又 , 对应的函数值分别是 , ,若 ,则有( )A、 B、 C、 D、4. 已知点(﹣2,y1),(﹣3,y2),(2,y3)在函数y=﹣ 的图象上,则( )A、y1<y2<y3 B、y3<y2<y1 C、y3<y1<y2 D、y2<y1<y35. 如图,在平面直角坐标系中,点O为坐标原点,点A(﹣3,0)和点B(0,2)都在坐标轴上,若反比例函数y= 的图象经过矩形AOBC的对称中心,则k的值为( )
2. 关于反比例函数 的图象,下列说法正确的是( )A、 随着 的增大而增大 B、图象分布在一三象限 C、当 时, D、若 在该图象上,则 也在该图象上3. 已知函数 ,又 , 对应的函数值分别是 , ,若 ,则有( )A、 B、 C、 D、4. 已知点(﹣2,y1),(﹣3,y2),(2,y3)在函数y=﹣ 的图象上,则( )A、y1<y2<y3 B、y3<y2<y1 C、y3<y1<y2 D、y2<y1<y35. 如图,在平面直角坐标系中,点O为坐标原点,点A(﹣3,0)和点B(0,2)都在坐标轴上,若反比例函数y= 的图象经过矩形AOBC的对称中心,则k的值为( )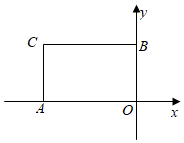 A、3 B、﹣3 C、1.5 D、﹣1.56. 反比例函数的图象经过(﹣1,3)点,则这个反比例函数的表达式为( )A、y=﹣ B、y= C、y=﹣ D、y=7. 点A(x1 , y1),B(x2 , y2),C(x3 , y3)在反比例函数y= 的图象上,若x1<x2<0<x3 , 则y1 , y2 , y3的大小关系是( )A、y1>y2>y3 B、y3>y2>y1 C、y2>y1>y3 D、y3>y1>y28. 下列关于反比例函数 ,说法不正确的是( )A、点(-2,1)、(-1,2)均在其图象上 B、双曲线分布在二、四象限 C、该函数图象上有两点A 、B ,若 < ,则 < D、当 时,x的范围是0 < x < 19. 反比例函数的图象如图所示,则这个反比例函数的表达式可能是( )
A、3 B、﹣3 C、1.5 D、﹣1.56. 反比例函数的图象经过(﹣1,3)点,则这个反比例函数的表达式为( )A、y=﹣ B、y= C、y=﹣ D、y=7. 点A(x1 , y1),B(x2 , y2),C(x3 , y3)在反比例函数y= 的图象上,若x1<x2<0<x3 , 则y1 , y2 , y3的大小关系是( )A、y1>y2>y3 B、y3>y2>y1 C、y2>y1>y3 D、y3>y1>y28. 下列关于反比例函数 ,说法不正确的是( )A、点(-2,1)、(-1,2)均在其图象上 B、双曲线分布在二、四象限 C、该函数图象上有两点A 、B ,若 < ,则 < D、当 时,x的范围是0 < x < 19. 反比例函数的图象如图所示,则这个反比例函数的表达式可能是( )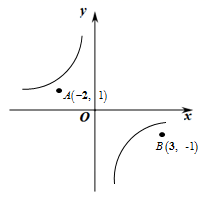 A、 B、 C、 D、10. 反比例函数 的图象如图所示,当 时, 的取值范围是( )
A、 B、 C、 D、10. 反比例函数 的图象如图所示,当 时, 的取值范围是( )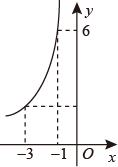 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 已知一个函数的图象与 的图象关于 轴成轴对称,则该函数的表达式为.12. 函数 为常数)的图象上有三点 ,则函数值 的大小关系是(用“<"连接).13. 已知反比例函数的图象位于第二、四象限,则k的取值范围是 .14. 如图,在平面直角坐标系中,等腰Rt△ABC的顶点A、B分别在x轴、y轴上,反比例函数y= (k>0,x>0)的图象经过直角顶点C.若OA=7,OB=3,则k的值为 .
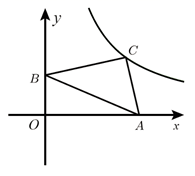 15. 如图,过原点的直线交反比例函数 图象于 , 两点,过点 分别作 轴, 轴的垂线,交反比例函数 ( )的图象于 , 两点.若 ,则图中阴影部分的面积为.
15. 如图,过原点的直线交反比例函数 图象于 , 两点,过点 分别作 轴, 轴的垂线,交反比例函数 ( )的图象于 , 两点.若 ,则图中阴影部分的面积为.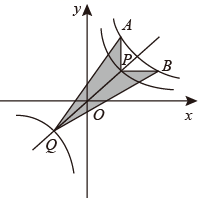 16. 反比例函数y= ,当1≤x≤3时,函数y的最大值和最小值之差为4,则k=.
16. 反比例函数y= ,当1≤x≤3时,函数y的最大值和最小值之差为4,则k=.三、解答题
-
17. 某车队要把4000吨货物运到雅安地震灾区(方案定后,每天的运量不变)。
(1)、从运输开始,每天运输的货物吨数n(单位:吨)与运输时间t(单位:天)之间有怎样的函数关系式?
(2)、因地震,到灾区的道路受阻,实际每天比原计划少运20%,则推迟1天完成任务,求原计划完成任务的天数.18. 如图,在平面直角坐标系中,正比例函数y=kx(k>0)与反比例函数y= 的图象分别交于A、C两点,已知点B与点D关于坐标原点O成中心对称,且点B的坐标为(m , 0).其中m>0. (1)、四边形ABCD的是 . (填写四边形ABCD的形状)(2)、当点A的坐标为(n , 3)时,四边形ABCD是矩形,求mn的值.
(1)、四边形ABCD的是 . (填写四边形ABCD的形状)(2)、当点A的坐标为(n , 3)时,四边形ABCD是矩形,求mn的值.
(3)、试探究:随着k与m的变化,四边形ABCD能不能成为菱形?若能,请直接写出k的值;若不能,请说明理由.
19. 如图,一次函数 的图象与反比例函数 的图象交于点A﹙−2,−5﹚、C﹙5,n﹚,交y轴于点B,交x轴于点D.
 (1)、求反比例函数 和一次函数 的表达式;(2)、连接OA、OC.求△AOC的面积.
(1)、求反比例函数 和一次函数 的表达式;(2)、连接OA、OC.求△AOC的面积.
20. 如图,已知A(﹣4,),B(﹣1,2)是一次函数y=kx+b与反比例函数y=(m≠0,x<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.(1)根据图象直接回答:在第二象限内,当x取何值时,一次函数大于反比例函数的值?
(2)求一次函数解析式及m的值;
(3)P是线段AB上的一点,连接PC,PD,若△PCA和△PDB面积相等,求点P坐标.
 21. 已知反比例函数y= (k为常数,k≠0)的图象经过点A(2,3).
21. 已知反比例函数y= (k为常数,k≠0)的图象经过点A(2,3).(Ⅰ)求这个函数的解析式;
(Ⅱ)判断点B(﹣1,6),C(3,2)是否在这个函数的图象上,并说明理由;
(Ⅲ)当﹣3<x<﹣1时,求y的取值范围.
22. 某乡镇要在生活垃圾存放区建一个老年活动中心,这样必须把1200立方米的生活垃圾运走:(1)假如每天能运x立方米,所需时间为y天,写出y与x之间的函数表达式;
(2)若每辆拖拉机一天能运12立方米,则5辆这样的拖拉机要用多少天才能运完?
(3)在(2)的情况下,运了8天后,剩下的任务要在不超过6天的时间内完成,那么至少需要增加多少辆这样的拖拉机才能按时完成任务?
四、综合题
-
23. 如图,在直角坐标平面内,正比例函数的图像与一个反比例函数图象在第一象限内的交点为点A,过点A作AB⊥x轴,垂足为点B,AB=3.
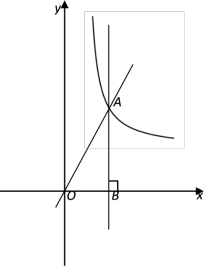 (1)、求反比例函数的解析式;(2)、在直线AB上是否存在点C,使点C到直线OA的距离等于它到点B的距离?若存在,求点C的坐标;若不存在,请说明理由;(3)、已知点P在直线AB上,如果△AOP是等腰三角形,请直接写出点P的坐标.24. 为了节能减排,某公司从2018年开始投入技术改进资金,经技术改进后产品的成本不断降低,具体数据如表:
(1)、求反比例函数的解析式;(2)、在直线AB上是否存在点C,使点C到直线OA的距离等于它到点B的距离?若存在,求点C的坐标;若不存在,请说明理由;(3)、已知点P在直线AB上,如果△AOP是等腰三角形,请直接写出点P的坐标.24. 为了节能减排,某公司从2018年开始投入技术改进资金,经技术改进后产品的成本不断降低,具体数据如表:年度
2018
2019
2020
2021
投入技术改进资金x万元
2.5
3
4
4.5
产品成本y万元
14.4
12
9
8
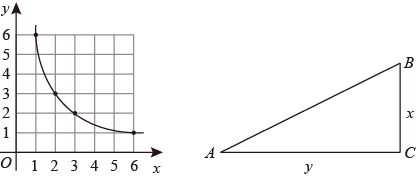
(1)、分析表中数据,请从一次函数和反比例函数中确定一个函数表示其变化规律,求出y与x的函数关系式,并说明理由;(2)、若2022年公司打算投入技术改进资金5万元,预计2022年产品成本比2021年降低多少万元?(3)、若2023年公司打算把投入技术改进资金x和产品成本y之和控制在12万元,请分别求出投入技术改进资金和产品成本.25. 阅读材料:已知:一次函数y=﹣x+b与反比例函数y= (x>0),当两个函数的图象有交点时,求b的取值范围.
 (1)、方方给出了下列解答:
(1)、方方给出了下列解答:﹣x+b=
x2﹣bx+4=0
∵两个函数有交点
∴△=b2﹣16≥0
但是方方遇到了困难:利用已学的知识无法解b2﹣16≥0这个不等式;
此时,圆圆提供了另一种解题思路;
第1步:先求出两个函数图象只有一个交点时,b= ▲ ;
第2步:画出只有一个交点时两函数的图象(请帮圆圆在直角坐标系中画出图象);
第3步:通过平移y=﹣x+b的图象,观察得出两个函数的图象有交点时b的取值范围是 ▲ .
应用:
如图,Rt△ABC中,∠C=90°,BC的长为x,AC的长为y,且S△ABC=12.
(2)、求y关于x的函数表达式;(3)、设x+y=m,求m的取值范围.