2022年浙教版数学八下期末复习阶梯训练：特殊平行四边形（优生加练）
试卷日期：2022-04-03 考试类型：复习试卷
一、单选题
-
1. 如图，在正方形ABCD中，点P在对角线BD上，PE⊥BC，PF⊥CD，E，F分别为垂足，连结AP，EF，则下列命题：①若AP=5，则EF=5；②若AP⊥BD，则EF∥BD；③若正方形边长为4，则EF的最小值为2，其中正确的命题是（ ）
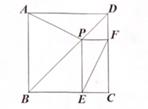A、①② B、①③ C、②③ D、①②③2. 如图，正方形ABCD的边长为a，P是对角线AC上的点，连结PB，过点P作PQ⊥BP交线段CD于点Q。当DQ=2CQ时，BP的长为（ ）
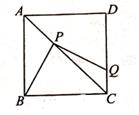A、 B、 C、 D、3. 在正方形ABCD的对角线BD上取一点E，连结AE，过点E作EF⊥AE交BC于点F，将线段EF向右平移m个单位，使得点E落在CD上，F落在BC上，已知AE+EF+CF=24，CD=10，则m的值为（ ）
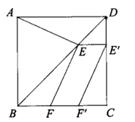A、6 B、4 -2 C、4 D、2 +24. 如图，在菱形 中，M、N分别是 和 的中点， 于点P，连接 ，若 ，则 （ ）
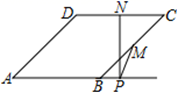A、 B、 C、 D、5. 如图， 、 是正方形 的边 上的两个动点，满足 ，连接 交 于点 ，连接 交 于点 ，连接 ，若正方形的边长为2，则线段 的最小值是（ ）
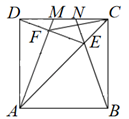A、2 B、1 C、 D、6. 如图，在正方形ABCD中，G是对角线BD上的一点，GE⊥CD ， GF⊥BC ， E ， F分别为垂足，连结AG ． 若AG＝8，四边形CEGF的面积为18，则该正方形的边长为（ ）
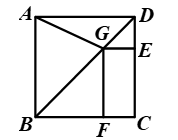A、10 B、12 C、5＋2 D、12－7. 如图，正方形ABCD中，E、F均为中点，则下列结论中：①AF⊥DE； ②AD=BP； ③PE+PF= PC； ④PE+PF=PC.其中正确的是（ ）
A、①④ B、①②④ C、①③ D、①②③8. 如图，在△ABC中，AB＝3，AC＝4，BC＝5，P为边BC上一动点，PE⊥AB于点E，PF⊥AC于点F，则EF的最小值为（ ）
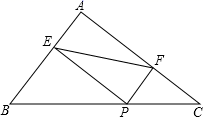A、2 B、2.4 C、3.2 D、3.69. 如图，在Rt△ABC中，∠ACB＝90°，AC＝4，AB＝6，分别以AB，AC，BC为边在AB的同侧作正方形ABEF，ACPQ，BCMN，四块阴影部分的面积分别为S1 ， S2 ， S3 ， S4 ， 则S1﹣S2+S3+S4的值是（ ）
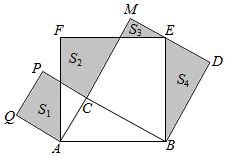A、12 B、24 C、 D、10. 如图所示，E、F分别是正方形ABCD的边CD和AD上的点且CE=DF，AE、BF相交于点O，下列结论：①AE=BF；②AE⊥BF；③AO=OE；SΔAOB=S四边形DEOF；⑤∠BAE=∠AFB，其中正确的有（ ）
A、2个 B、3个 C、4个 D、5个二、填空题
-
11. 如图，C为线段 上一动点，分别过B，D作 ， ，连接 ， ，已知 ， ， ，设 .请用含x的代数式表示 的长为 ， 根据上述方法，求出 的最小值为.
12. 如图，长方形ABCD中，AD＝8，AB＝4，BQ＝5，点P在AD边上运动，当△BPQ为等腰三角形时，AP的长为 ．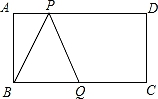
13. 我国古代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”，它是由4个全等的直角三角形与1个小正方形拼成的一个大正方形，已知大正方形的面积为25.小正方形的面积为3.
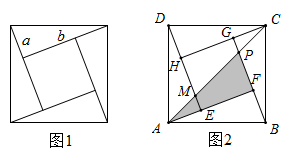(1)、如图1，若用a，b表示直角三角形的两条直角边 ， .(2)、如图2，若拼成的大正方形为正方形 ，中间的小正方形为正方形 ，连接 ，交 于点P，交 于点M， .14. 如图，在直角三角形 中，直角边 ， ，以它的三边分别作出了正方形 、 、 ，把 、 、 的面积分别记为 、 、 ，则 .
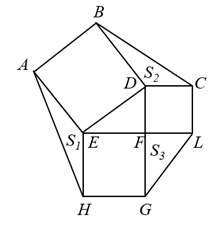15. 如图，在矩形ABCD中，AB＝4，BC＝8，E为CD边的中点，若P、Q为BC边上的两个动点，且PQ＝2，四边形APQE的周长最小值为.
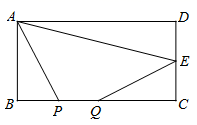16. 如图，正方形 的边长为 ， 为 上一点，且 ， 为 边上的一个动点连接 ，以 为边向右侧作等边 ，连接 ，则 的最小值为.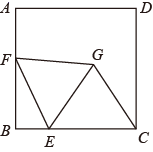
三、解答题
-
17. 如图，在矩形 中， ， ，若点M、N分别是线段 、 上的两个动点，则求 的最小值.
18. 如图，在平面直角坐标系中长方形ABCO的顶点A，C的坐标分别为(0，8) ，(20，0)，D是OC的中点，点P在AB上运动，当△ODP是腰长为10的等腰三角形时，求点P的坐标.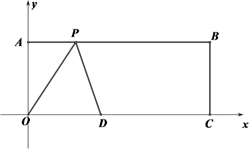
19. 如图，在平行四边形ABCD中，BF平分∠ABC交AD于点F，AE⊥BF于点O，交BC于点E，连接EF．求证：四边形ABEF是菱形；
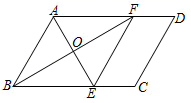20. 如图，在平面直角坐标系中，矩形OABC的顶点A、C的坐标分别为（10，0），（0，4），点D是OA的中点，点P在BC上运动，当△ODP是腰长为5的等腰三角形时，求点P的坐标.
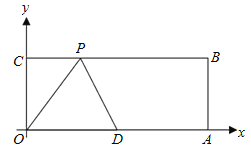21. 如图1，点C在线段AB上，分别以AC、BC为边在线段AB的同侧作正方形ACDE和正方形BCMN，连结AM、BD．
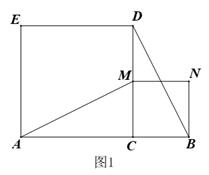(1)、AM与BD的关系是： ．(2)、如果将正方形BCMN绕点C顺时针旋转锐角α，它不变（如图2）．（1）中所得的结论是否仍然成立？请说明理由．
(3)、在（2）的条件下，连接AB、DM，若AC＝4，BC＝2，求 的值．22. 如图，△ABC中，点O为AC边上的一个动点，过点O作直线MN∥BC，设MN交∠BCA的外角平分线CF于点F，交∠ACB内角平分线CE于E.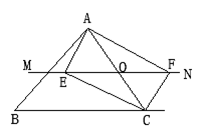
(1)、求证：EO=FO；(2)、当点O运动到何处时，四边形AECF是矩形？并证明你的结论；(3)、若AC边上存在点O，使四边形AECF是正方形，猜想△ABC的形状并证明你的结论。四、综合题
-
23. 对于平面直角坐标系xOy中的线段AB和点M，给出定义：若M满足：MA＝MB，则称M是线段AB的“对称点”，其中，当0°＜∠AMB＜90°，称M为线段AB的“劣对称点”；当90°≤∠AMB≤180°时，则称M为“优对称点”.
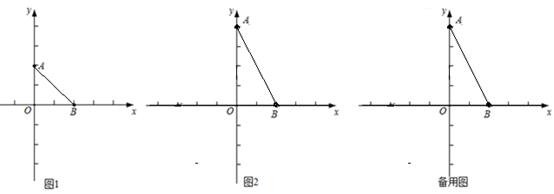(1)、如图1，点A，B的坐标分别为（0，2），（2，0），则在坐标M1（0，0），M2（2，3），M3（4，4）中，是线段AB的“对称点”为：；是线段AB的“劣对称点”为.(2)、如图2，点A的坐标为（0，4），点B的坐标为（2，0），若M为线段AB的“优对称点民主点”，求出点M的横坐标m的取值范围；(3)、在（2）的条件下，点P为x轴上的动点（不与B重合），若T为AB的“对称点”，当线段TB与TP的和最小时，直接写出T关于直线AB的对称点S的坐标.24. 如图，四边形ABCD中，AB∥CD，∠C＝110°.E为BC的中点，直线FG经过点E，DG⊥FG于点G，BF⊥FG于点F.
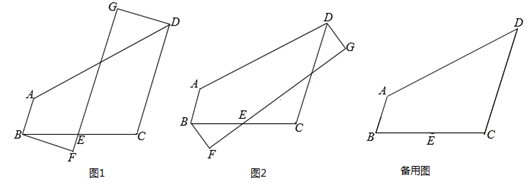(1)、如图1，当∠BEF＝70°时，求证：DG＝BF；(2)、如图2，当∠BEF≠70°时，若BC＝DC，DG＝BF，请直接写出∠BEF的度数；(3)、当DG－BF的值最大时，直接写出∠BEF的度数.25. 如图，在平面直角坐标系中，直线AB：y＝ x＋m与x轴交于点A，与y轴交于点B（0，2），直线AC经过y轴负半轴上的点C，且OA＝OC.
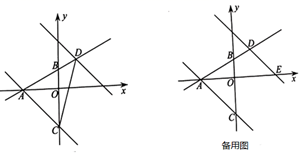(1)、求直线AC的函数表达式；(2)、直线AC向上平移9个单位，平移后的直线与直线AB交于点D，连结DC，求△ACD面积；(3)、在（2）的条件下，平移后的直线与x轴交于点E，点M为直线AB上的一点，在平面直角坐标系中是否存在点N，使以点E，D，M，N为顶点的四边形是矩形，若存在，请直接写出点N的坐标；若不存在，请说明理由.