2022年浙教版数学八下期末复习阶梯训练：特殊平行四边形（提高训练）
试卷日期：2022-04-03 考试类型：复习试卷
一、单选题
-
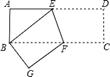
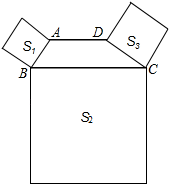
1. 一个长方形的周长为28厘米，长的2倍比宽的3倍多3厘米，则这个长方形的面积是（ ）A、45平方厘米 B、35平方厘米 C、25平方厘米 D、20平方厘米2. 如图，四边形ABCD中，AD∥BC，∠ABC+∠DCB＝90°，且BC＝2AD，以AB、BC、DC为边向外作正方形，其面积分别为S1、S2、S3 ， 若S1＝4，S3＝12，则S2的值为（ ）
A、16 B、24 C、48 D、643. 已知四边形ABCD是平行四边形，下列说法：①当 时，它是矩形；② 时，它是菱形；③当 时，它是菱形；④当 时，它是正方形.其中正确的有（ ）A、①② B、②④ C、③④ D、②4. 如图，某自动感应门的正上方 处装着一个感应器，离地 米，当人体进入感应器的感应范围内时，感应门就会自动打开．一个身高1.6米的学生 正对门，缓慢走到离门1.2米的地方时 米），感应门自动打开，则人头顶离感应器的距离 等于
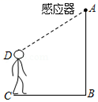A、1.2米 B、1.5米 C、2.0米 D、2.5米5. 如图，在菱形ABCD中， AB=4，∠B=60°，AE⊥BC，AF⊥CD ，垂足分别为点E，F，连结EF，则 △AEF 的面积是（ ）
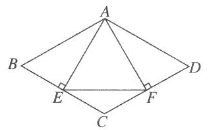A、 B、 C、 D、6. 如图所示，在菱形ABCD中，对角线AC，BD相交于点O，E为BC的中点，连结OE，则OE的长一定等于（ ）
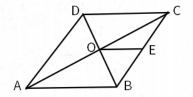A、BE B、AO C、AD D、OB7. 如图，四边形ABCD是正方形，BE⊥EF，DF⊥EF，BE=2.5dm，DF=4dm，那么EF的长为（ ）
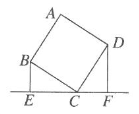A、6.5dm B、6dm C、5.5dm D、4dm8. 如图所示，在 ABCD中，E为BC边上一点，以AE为边作正方形AEFG，若∠BAE=40°，∠CEF=15°，则∠D的度数是（ ）
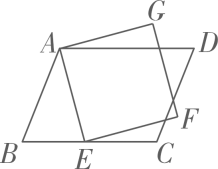A、65° B、55° C、70° D、75°9. 在▱ABCD中，AB=3，BC=4，当口ABCD的面积最大时，下列结论：①AC=5；②∠A+∠C=180°；③AC⊥BD；④AC=BD.其中正确的有（ ）A、①②③ B、①②④ C、②③④ D、①③④10. 《九章算术》是中国传统数学中最早记载无理数的著作.书中对开方开不尽的数叫做“面”.例如面积为3的正方形的边长为3“面”，关于3“面”的说法正确的是（ ）A、它是无限循环小数 B、它是0和1之间的实数 C、它不存在 D、它是1和2之间的实数二、填空题
-
11. 如图，一个正方形摆放在桌面上，那么这个正方形的边长为 ．
12. 如图，图形的各个顶点都在33正方形网格的格点上.则.
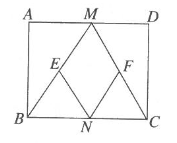
13. 如图所示，在矩形ABCD中，CE⊥BD，点E为垂足，连结AE，若∠DCE：∠ECB=3：1，则∠ACE=.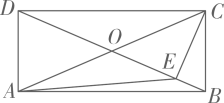
14. 在△ABC中，点D，E，F分别在BC，AB，CA上，且DE//CA，DF//BA，有下列说法：①如果∠BAC=90°，那么四边形AEDF是矩形；②如果AD平分∠BAC，那么四边形AEDF是菱形；③如果AD⊥BC且AB=AC，那么四边形AEDF是菱形；④如果AD⊥BC且AB=AC，那么四边形AEDF是正方形，其中正确的有.(填序号)
15. 三国时期，数学家赵爽绘制了“勾股圆方图”，又叫“赵爽弦图”，如图所示，△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形，四边形ABCD和四边形EFGH都是正方形，如果EF＝2，AH＝6，那么四边形ABCD的面积等于.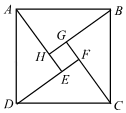
16. 如图，点E是矩形ABCD边AD上一点，点F，G，H分别是BE，BC，CE的中点，AF＝6，则GH的长为 ．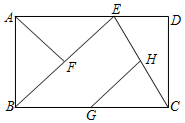
三、解答题
-
17. 如图，在四边形 中， 是 的垂直平分线， 是 上一点， 交 于 ，连接 ． ，试证明四边形 是菱形．
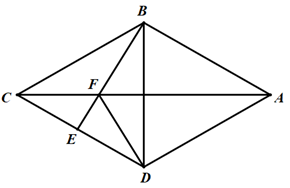18. 如图，在 中，AF ， BH ， CH ， DF分别是 ， ， 与 的平分线，AF与BH交于点E ， CH与DF交于点G ．求证： ．
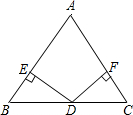
19. 如图，四边形 是菱形，对角线 cm， cm， 于 ，求 的长．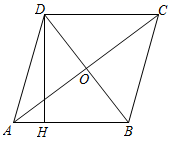
20. 如图，△ABC中，AB＝AC ， AD平分∠BAC交BC于点D ， AE平分∠BAC的外角，且∠AEB＝90°．求证：四边形ADBE是矩形．
21. 已知四边形 是菱形， 、 、 、 、分别是菱形 各边的中点，连接 、 、 、 ，判断四边形 的形状，并说明理由.
22. 如图，在菱形 中，点 ， 分别在边 ， 上，且 .求证： .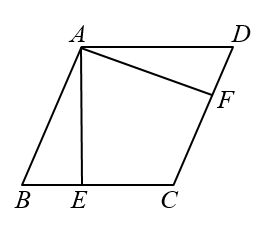
四、综合题
