高中数学人教A版（2019）选修三第七章离散型随机变量及其分布

试卷日期：2022-04-01 考试类型：同步测试

前去【出卷网】下载

一、单选题

1. 已知随机变量X，Y满足 $Y = 2 X + 3$ ， Y的期望 $E (Y) = \frac{7}{3}$ ， X的分布列为：
X
-1
0
1
P
$\frac{1}{2}$
a
b
则a，b的值分别为（）

A、 $a = \frac{1}{6} ， b = \frac{1}{3}$ B、 $a = \frac{1}{4} ， b = \frac{1}{4}$ C、 $a = \frac{1}{3} ， b = \frac{1}{6}$ D、 $a = \frac{3}{8} ， b = \frac{1}{8}$

查看试题解析
2. 已知某批零件的长度（单位：毫米）服从正态分布 $N (100 ， 3^{2})$ ，从中随机抽取一件，其长度落在区间 $(103 ， 106)$ 内的概率为（）
（附：若随机变量 $ξ$ 服从正态分布 $N (μ ， σ^{2})$ ，则 $P (μ - σ < ξ < μ - σ) = 68.26 %$ ， $P (μ - 2 σ < ξ < μ - 2 σ) = 95.44 %$ ）

A、4.56% B、13.59% C、27.18% D、31.74%

查看试题解析
3. 设随机变量 $ξ ∼ B (2 ， p) ， η ∼ B (4 ， p)$ ，若 $P (ξ \geq 1) = \frac{5}{9}$ ，则 $P (η \geq 2)$ 的值为（）

A、 $\frac{32}{81}$ B、 $\frac{11}{27}$ C、 $\frac{65}{81}$ D、 $\frac{16}{81}$

查看试题解析
4. 已知随机变量X，Y分别满足，X～B（8，p），Y～N（μ， $σ^{2}$ ），且期望E（X）=E（Y），又P（Y≥3）= $\frac{1}{2}$ ，则p=（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{3}{8}$ D、 $\frac{1}{2}$

查看试题解析
5. 某校高三有1000人参加考试，统计发现数学成绩近似服从正态分布N(105，σ²)，且成绩优良（不低于120分）的人数为360，则此次考试数学成绩及格（不低于90分）的人数约为（）

A、360 B、640 C、720 D、780

查看试题解析
6. 随机变量ξ的分布列如下表：
ξ
1
a
9
P
b
$1 - 2 b$
b
其中 $1 < a < 9$ ， $0 < b < \frac{1}{2}$ ，则下列说法正确的是（）

A、若 $a = 5$ ，则当 $0 < b < \frac{1}{2}$ 时， $E (ξ)$ 随b的增大而增大 B、若 $a = 5$ ，则当 $0 < b < \frac{1}{2}$ 时， $E (ξ)$ 随b的增大而减小 C、若 $b = \frac{1}{3}$ ，则当 $a = 5$ 时， $D (ξ)$ 有最小值 D、若 $b = \frac{1}{3}$ ，则当 $a = 5$ 时， $D (ξ)$ 有最大值

查看试题解析
7. 已知甲盒子中有3个红球，1个白球，乙盒子中有2个红球，2个白球，同时从甲，乙两个盒子中取出i个球进行交换，交换后，分别记甲、乙两个盒中红球个数 $ξ_{i} ， η_{i} (i = 1 ， 2)$ ，则（）

A、 $E (ξ_{1}) = E (η_{1})$ B、 $E (ξ_{1}) < E (η_{1})$ C、 $E (ξ_{2}) = E (η_{2})$ D、 $E (ξ_{2}) < E (η_{2})$

查看试题解析
8. 下列说法正确的有（）

A、两个随机变量的线性相关性越强，则相关系数 $r$ 的绝对值越接近于0 B、若 $X$ 是随机变量，则 $E (2 X + 1) = 2 E (X) + 1 ， D (2 X + 1) = 4 D (X) + 1$ . C、已知随机变量 $ξ ∼ N (0 ， 1)$ ，若 $P (ξ > 1) = p$ ，则 $P (ξ > - 1) = 1 - 2 p$ D、设随机变量 $ξ$ 表示发生概率为 $p$ 的事件在一次随机实验中发生的次数，则 $D (ξ) \leq \frac{1}{4}$

查看试题解析

二、多选题

9. 已知随机事件A，B发生的概率分别为 $P (A) = 0.3 ， P (B) = 0.6$ ，下列说法正确的有（）

A、若 $P (A B) = 0.18$ ，则A，B相互独立 B、若A，B相互独立，则 $P (B | A) = 0.6$ C、若 $P (B | A) = 0.4$ ，则 $P (A B) = 0.12$ D、若 $A \subseteq B$ ，则 $P (A | B) = 0.3$

查看试题解析
10. 已知甲盒中有1个白球和2个黑球，乙盒中有2个白球和3个黑球，从乙盒中随机抽取 $i (i = 1 ， 2)$ 个球放入甲盒中．放入i个球后，甲盒中含有黑球的个数记为 $x_{i} (i = 1 ， 2)$ ，现从甲盒中取1个球是黑球的概率记为 $P_{i} (i = 1 ， 2)$ ，则（）

A、 $P_{1} < P_{2}$ B、 $P_{1} > P_{2}$ C、 $E (x_{2}) < E (x_{1})$ D、 $E (x_{2}) > E (x_{1})$

查看试题解析
11. 下列说法正确的是（）

A、设离散型随机变量X等可能取1，2，3，…，n，若 $P (X < 4) = 0.3$ ，则 $n = 10$ B、设随机变量X服从二项分布 $B (6 ， \frac{1}{2})$ ，则 $P (X = 2) = \frac{15}{32}$ C、设离散型随机变量 $η$ 服从两点分布，若 $P (η = 1) = 2 P (η = 0)$ ，则 $P (η = 0) = \frac{1}{3}$ D、设随机变量x服从正态分布 $N (2 ， σ^{2})$ 且 $P (X < 4) = 0.9$ ，则 $P (0 < X < 2) = 0.3$

查看试题解析

12. 设随机变量

ξ

的分布列如下：

$ξ$	1	2	3	4	5	6	7	8	9	10
$P$	$a_{1}$	$a_{2}$	$a_{3}$	$a_{4}$	$a_{5}$	$a_{6}$	$a_{7}$	$a_{8}$	$a_{9}$	$a_{10}$

则（）

A、当

{a_{n}}

为等差数列时，

a_{3} + a_{6} = \frac{1}{6}

B、数列

{a_{n}}

的通项公式可能为

a_{n} = \frac{11}{10 n (n + 1)}

C、当数列

{a_{n}}

满足

a_{n} = \frac{1}{2^{n}} (n = 1 ， 2 ， \cdot \cdot \cdot ， 9)

时，

a_{10} = \frac{1}{2^{9}}

D、当数列

{a_{n}}

满足

P (ξ \leq k) = k^{2} a_{k} (k = 1 ， 2 ， 3 ， \cdot \cdot \cdot ， 10)

时，

a_{n} = \frac{11}{10 n (n + 1)}

查看试题解析

三、填空题

13. 为了弘扬中华民族敬老爱老的传统美德，切实关爱社区老年人的身体健康，社区卫生服务中心联合医院为老年人进行免费体检，并送上健康的祝福.已知重阳节当天，医院彩超室接待了80岁以上的老年人5位，70岁到80岁之间的老年人3位，为了进一步了解各年龄阶段老年人的健康情况，现从8人中随机抽取3人，则抽取的3人中80岁以上的老年人人数的数学期望为.

查看试题解析
14. 甲、乙两名运动员在羽毛球场进行羽毛球比赛，已知每局比赛甲胜的概率为P，乙胜的概率为1-p，且各局比赛结果相互独立.当比赛采取5局3胜制时，甲用4局赢得比赛的概率为 $\frac{8}{27}$ .现甲、乙进行7局比赛，采取7局4胜制，则甲获胜时比赛局数X的数学期望为

查看试题解析
15. 已知 $X \sim B (3 ， \frac{3}{5})$ ，且 $Y = - 5 X + 2$ ，则 $Y$ 的方差为．

查看试题解析
16. 在射击训练中，某射击运动员一次射击命中的概率为 $\frac{9}{10}$ ，连续两次射击命中的概率为 $\frac{4}{5}$ .已知他第一发子弹命中，则他第二发子弹命中的概率为.

查看试题解析

四、解答题

17. 为了买到包括星黛露毛线玩具，达菲雪莉玫和星黛露毛绒玩具钥匙圈等商品，12月29日凌晨，约5000名游客在上海迪士尼外夜排长龙，此现象在网络上引发了广泛讨论.为了解广大民对下通玩偶的喜爱程度，某市一玩具商城随机抽取了100名市民，以分数表示对卡通玩偶的喜爱程度（喜爱程度越高，分数越高，满分为100分）到如下频率分布直方图.

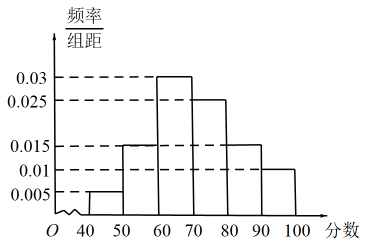(1)、试估计该市市民对卡通玩偶平均喜爱程度的分数值；

(2)、用上述100名市民对玩偶喜爱程度分数值的频率分布估算所有排队游客分数值的概率分布，在所有游客中随机抽取2人，对分数值在区间 $[70 ， 80)$ 内的游客送一个玩偶，分数值在区间 $[80 ， 100]$ 内的游客赠送两个玩偶，分数值低于70分的游客不送玩偶，记总共送出的玩偶个数为 $X$ ，求 $E (X)$ .

查看试题解析
18. 2022年2月4日至2月20日，第24届冬季奥林匹克运动会在北京和张家口隆重举行.北京市各校大学生争相出征服务冬奥会，经统计某校在校大学生有9000人，男生与女生的人数之比是2：1，按性别用分层抽样的方法从该校大学生中抽取9名参加冬奥会比赛场馆服务培训，培训分4天完成，每天奖励若干名“优秀学员”，累计获2次或2次以上者可获2022冬奥会吉祥物“冰墩墩”或“雪容融”一个.

(1)、若从这抽取的9名大学生中随机选出3人服务“国家体育馆”，求选出的3人中至少有一位是女生的概率.

(2)、设参加服务培训的大学生甲每天获“优秀学员”奖励的概率均为 $\frac{2}{3}$ ，记同学甲获得“优秀学员”的次数为X，试求X的分布列及其数学期望 $E (X)$ ，并以获得“优秀学员”的次数期望为参考，试预测该同学甲能否获得冬奥会吉祥物？

查看试题解析
19. 将8株某种果树的幼苗分种在4个坑内，每坑种2株，每株幼苗成活的概率为0.5.若一个坑内至少有1株幼苗成活，则这个坑不需要补种，若一个坑内的幼苗都没成活，则这个坑需要补种，每补种1个坑需15元，用X表示补种费用.

(1)、求一个坑不需要补种的概率；

(2)、求4个坑中恰有2个坑需要补种的概率；

(3)、求X的数学期望.

查看试题解析
20. “双减”政策实施以来，各地纷纷推行课后服务“5+2"模式，即学校每周周一至周五5天都要面向所有学生提供课后服务，每天至少2小时．某学校的课后服务有学业辅导体育锻炼、实践能力创新培养三大类别，为了解该校学生上个月参加课后服务的情况，该校从全校学生中随机抽取了100人作为样本．发现样本中未参加任何课后服务的有14人，样本中仅参加某一类课后服务的学生分布情况如下：
每周参加活动天数
课后服务活动
1天
2~4天
5天
仅参加学业辅导
10人
11人
4人
仅参加体育锻炼
5人
12人
1人
仅参加实践能力创新培养
3人
12人
1人

(1)、从全校学生中随机抽取1人．估计该学生上个月至少参加了两类课后服务活动的概率；

(2)、从全校学生中随机抽取3人．以频率估计概率，以X表示这3人中上个月仅参加学业辅导的人数．求X的分布列和数学期望；

(3)、老样本中上个月未参加任何课后服务的学生有 $n (0 < n \leq 14)$ 人在本月选择仅参加学业辅导．样本中其他学生参加课后服务的情况在本月没有变化．从全校学生中随机抽取3人．以频率估计概率，以X表示这3人中上个月仅参加学业辅导的人数，以Y表示这3人中本月仅参加学业辅导的人数．试判断方差 $D (X)$ 、 $D (Y)$ 的大小关系（结论不要求证明）．

查看试题解析
21. 2022年冬奥会在北京举行，冬奥会吉祥物“冰墩墩”自亮相以来就好评不断，出现了“一墩难求”的现象.主办方现委托某公司推出一款以“冰墩墩”为原型的纪念品在专卖店进行售卖.已知这款纪念品的生产成本为80元/件，为了确定其销售价格，调查了对这款纪念品有购买意向的消费者（以下把对该纪念品有购买意向的消费者简称为消费者）的心理价位，并将收集的100名消费者的心理价位整理如下：
心理价位（元/件）
90
100
110
120
人数
10
20
50
20
假设当且仅当这款纪念品的销售价格小于或等于某位消费者的心理价位时，该消费者就会购买该纪念品.公司为了满足更多消费者的需求，规定每位消费者最多只能购买一件该纪念品.设这款纪念品的销售价格为x（单位：元/件）， $90 < x \leq 120$ ，且每位消费者是否购买该纪念品相互独立.用样本的频率分布估计总体的分布，频率视为概率.

(1)、若 $x = 100$ ，试估计消费者购买该纪念品的概率；已知某时段有4名消费者进店，X为这一时段该纪念品的购买人数，试求X的分布列和数学期望 $E (X)$ ；

(2)、假设共有M名消费者，设该公司售卖这款纪念品所得总利润为Y（单位：元），当该纪念品的销售价格x定为多少时，Y的数学期望 $E (Y)$ 达到最大值？

查看试题解析
22. 中医药传承数千年，治病救人济苍生.中国工程院院士张伯礼在接受记者采访时说：“中医药在治疗新冠肺炎中发挥了核心作用，能显著降低轻症病人发展为重症病人的几率.对改善发热､咳嗽､乏力等症状，中药起效非常快，对肺部炎症的吸收和病毒转阴都有明显效果.”2021年12月某地爆发了新冠疫情，医护人员对确诊患者进行积极救治.现有6位症状相同的确诊患者，平均分成A，B两组，A组服用甲种中药，B组服用乙种中药.服药一个疗程后，A组中每人康复的概率都为 $\frac{13}{15}$ ， B组3人康复的概率分别为 $\frac{9}{10}$ ， $\frac{3}{4}$ ， $\frac{3}{4}$ .

(1)、设事件C表示A组中恰好有1人康复，事件D表示B组中恰好有1人康复，求 $P (C D)$ ；

(2)、若服药一个疗程后，每康复1人积2分，假设认定：积分期望值越高药性越好，请问甲､乙两种中药哪种药性更好？

查看试题解析

每周参加活动天数课后服务活动	1天	2~4天	5天
仅参加学业辅导	10人	11人	4人
仅参加体育锻炼	5人	12人	1人
仅参加实践能力创新培养	3人	12人	1人

X	-1	0	1
P	$\frac{1}{2}$	a	b

心理价位（元/件）	90	100	110	120
人数	10	20	50	20

高中数学人教A版（2019） 选修三 第七章 离散型随机变量及其分布

一、单选题

二、多选题

三、填空题

四、解答题

高中数学人教A版（2019）选修三第七章离散型随机变量及其分布