高中数学人教A版(2019) 必修二 解三角形月考试卷
试卷日期:2022-04-01 考试类型:月考试卷
一、单选题
-
1. 在 中,已知 , , ,则角C为( )A、 B、 C、 或 D、2. 在 中,若 ,则角 等于( )A、 B、 C、 D、3. 在 中,内角 , , 所对的边分别为 , , ,若 , ,当 有两解时, 的取值范围是( )A、 B、 C、 D、4. 的内角 , , 的对边分别为 , , ,若 , ,则 的值为( )A、2 B、 C、6 D、5. 在 中,内角 、 、 所对的边分别为 、 、 ,满足 ,则 =( )A、 B、 C、 D、6. 的内角 , , 的对边分别是 , , .已知 , , 边上的中线长度为 ,则 ( )A、 B、 C、1 D、7. 在 中,角 、 、 所对的边分别是 、 、 ,若 ,则 是( )A、等边三角形 B、有一内角是 的直角三角形 C、等腰直角三角形 D、有一内角是 的等腰三角形8. 在中,给出如下命题:
① 若 ,则 是锐角三角形
② 若 ,则 是等腰三角形
③ 若 ,则 是等腰直角三角形
④ 若 ,则 是等腰或直角三角形
其中,所有正确命题的序号是 ( )
A、①② B、②③ C、②④ D、③④二、多选题
-
9. 甲,乙两楼相距 ,从乙楼底仰望甲楼顶的仰角为 ,从甲楼顶望乙楼顶的俯角为 ,则下列说法正确的有( )A、甲楼的高度为 B、甲楼的高度为 C、乙楼的高度为 D、乙楼的高度为10. 若△ABC的内角A,B,C所对的边分别为a,b,c,且满足 ,则下列结论正确的是( )A、角C一定为锐角 B、a2 + 2b2 - c2 = 0 C、3tanA + tanC = 0 D、tanB的最大值为11. 在锐角 中,角A , B , C所对的边分别为a , b , c , 已知 ,且 ,则( )A、 B、角B的取值范围是 C、 的取值范围是 D、 的取值范围是12. 在平面直角坐标系 中, 的三个顶点O,A,B的坐标分别为 , , ,设 , , ,则( )A、 B、 C、 (R为 外接圆的半径) D、
三、填空题
-
13. 在△ABC中,D是AB的中点,∠ACD与∠CBD互为余角,AD=2,AC=3,则sinA的值为.14. 在 中, , , ,延长 到 ,使得 ,则 的长为 .15. 已知 的内角 , , 的对边分别为 , , ,点 在边 上,且 , , ,则 的面积的最大值为.16. 锐角 的内切圆的圆心为 ,内角 , , 所对的边分别为 , , .若 ,且 的外接圆半径为1,则 周长的取值范围为.
四、解答题
-
17. 如图,在 中,角A,B,C的对边分别为a,b,c,且满足asinB+bcosA=c ,线段BC的中点为D.
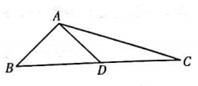 (1)、求角B的大小;(2)、已知 ,求 的大小.18. 记 是内角 , , 的对边分别为 , , .已知 ,点 在边 上, .(1)、证明: ;(2)、若 ,求 .19. 在 中,内角 , , 对应的边分别为 , , ,设 , ,且 .(1)、求 的值;(2)、若 , ,点 满足 ,求 的长.20. 在条件:① ,② ③ , .且 ,这三个条件中任选一个,补充在下面问题中:
(1)、求角B的大小;(2)、已知 ,求 的大小.18. 记 是内角 , , 的对边分别为 , , .已知 ,点 在边 上, .(1)、证明: ;(2)、若 ,求 .19. 在 中,内角 , , 对应的边分别为 , , ,设 , ,且 .(1)、求 的值;(2)、若 , ,点 满足 ,求 的长.20. 在条件:① ,② ③ , .且 ,这三个条件中任选一个,补充在下面问题中:中,内角 , , 所对边长分别是 , , .若 , , ▲ . 求 的面积.
(选择多个条件时,按你第一个选择结果给分)