高中数学人教A版(2019) 必修二 第六章 第四节 平面向量的应用
试卷日期:2022-03-26 考试类型:月考试卷
一、单选题
-
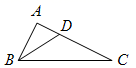
1. 在 中,内角 , , 的对边分别为 , , ,若 , , ,则 ( )A、3 B、2 C、1 D、2. 如图,已知 为 中 的角平分线,若 , ,则 ( )
 A、1 B、2 C、3 D、3. 在四边形 中, , , , ,则 的长为( )A、 B、 C、 D、4. 在 中,角 , , 所对的边分别为 , , ,且 , ,若满足条件的 有两个,则 的取值范围是( )A、 B、 C、 D、5. 在 中,内角A,B,C的对边分别是a,b,c,且 , ,则 的面积为( )A、 B、 C、 D、6. 如图,一辆汽车在一条水平的公路上向正西方向行驶,到 处时测得公路北侧一山顶 在西偏北45°的方向上,行驶 后到达 处,测得此山顶在西偏北75°的方向上,仰角为60°,则此山的高度 为( )
A、1 B、2 C、3 D、3. 在四边形 中, , , , ,则 的长为( )A、 B、 C、 D、4. 在 中,角 , , 所对的边分别为 , , ,且 , ,若满足条件的 有两个,则 的取值范围是( )A、 B、 C、 D、5. 在 中,内角A,B,C的对边分别是a,b,c,且 , ,则 的面积为( )A、 B、 C、 D、6. 如图,一辆汽车在一条水平的公路上向正西方向行驶,到 处时测得公路北侧一山顶 在西偏北45°的方向上,行驶 后到达 处,测得此山顶在西偏北75°的方向上,仰角为60°,则此山的高度 为( )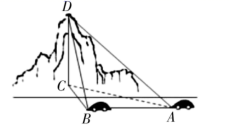 A、 B、 C、 D、6007. 已知 的内角 , , 所对的边分别为 , , ,若 , ,则 面积的最大值为( )A、 B、 C、 D、8. 在 中,A,B,C分别为 三边a,b,c所对的角.若 ,且满足关系式 ,则 ( )A、2 B、4 C、6 D、8
A、 B、 C、 D、6007. 已知 的内角 , , 所对的边分别为 , , ,若 , ,则 面积的最大值为( )A、 B、 C、 D、8. 在 中,A,B,C分别为 三边a,b,c所对的角.若 ,且满足关系式 ,则 ( )A、2 B、4 C、6 D、8二、多选题
-
9. 如图, 的三个内角 , , 对应的三条边分别是 , , , 为钝角, , , , ,则下列结论正确的有( )
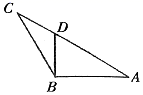 A、 B、 C、 D、 的面积为10. 已知 的三个内角 , , 所对的边分别为 , , ,则下列条件能推导出 一定是锐角三角形的是( )A、 B、 C、 D、11. 已知点 在 所在平面内,则( )A、满足 时, 是 的外心 B、满足 时, 是 的重心 C、满足 时, 是 的内心 D、满足 时, 是 的垂心12. 在△ 中, , , ,P为△ 内一点, ,下列结论正确的是( )A、若 ,则 B、若 ,则 C、△ 的面积的最大值为 D、△ 的面积的取值范围是
A、 B、 C、 D、 的面积为10. 已知 的三个内角 , , 所对的边分别为 , , ,则下列条件能推导出 一定是锐角三角形的是( )A、 B、 C、 D、11. 已知点 在 所在平面内,则( )A、满足 时, 是 的外心 B、满足 时, 是 的重心 C、满足 时, 是 的内心 D、满足 时, 是 的垂心12. 在△ 中, , , ,P为△ 内一点, ,下列结论正确的是( )A、若 ,则 B、若 ,则 C、△ 的面积的最大值为 D、△ 的面积的取值范围是三、填空题
-
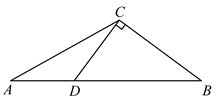
13. 在锐角 中,角 的对边分别为 ,若 , ,则边 的取值范围是 .14. 在 中,点D在边 上, ,则 的长为 .
 15. 在 中,角 , , 的对边分别是 , , ,若 ,则 .16. 在 中,角 、 、 所对的边分别为 、 、 , , ,若点 在边 上,并且 , 为 的外心,则 之长为 .
15. 在 中,角 , , 的对边分别是 , , ,若 ,则 .16. 在 中,角 、 、 所对的边分别为 、 、 , , ,若点 在边 上,并且 , 为 的外心,则 之长为 .四、解答题
-
17. 已知a,b,c是 的内角A,B,C的对边,且 .(1)、求角A的大小;(2)、若 , 的周长为 ,求c.18. 中,内角 , , 所对的边分别为 , , , , 且 .(1)、求的大小;(2)、若的周长为 , 求边上中线的长度.19. 已知 的内角 所对的边分别为 ,且__________.请从下面三个条件中任选一个,补充在题目的横线上,并作答.
① ;② :③ 的面积为 .
(1)、求角 的大小;(2)、若点 满足 ,且 ,求 的最小值.
