高中数学人教A版(2019) 必修二 第六章 第三节 平面向量的概念与运算
试卷日期:2022-03-26 考试类型:月考试卷
一、单选题
-
1. 已知△ 的边 上有一点 满足 ,则 可表示为( )A、 B、 C、 D、2. 已知向量 , .若 ,则实数 ( )A、2或-2 B、2 C、0 D、-23. 已知向量 , ,满足 ,且 ,则 ( )A、 B、 C、-3 D、4. 已知 , 为坐标原点,则下列说法正确的是( )A、 B、 三点共线 C、 三点共线 D、5. 已知向量 ,则下列结论不正确的是( )A、 B、 与 可以作为基底 C、 + = D、 ﹣ 与 方向相反6. 已知 , ,则 ( )A、 B、 C、 D、7. 已知向量 满足 ,且 ,则 与 的夹角 为( )A、 B、 C、 D、8. 设有四边形ABCD,O为空间任意一点,且 ,则四边形ABCD是( )A、空间四边形 B、平行四边形 C、等腰梯形 D、矩形9. 已知D,E为所在平面内的点,且 , , 若 , 则( )A、-3 B、3 C、 D、10. 已知正的边长为2,A,B分别在x轴,y轴的正半轴(含原点)上滑动,则的最大值是( )A、 B、3 C、2 D、11. 已知平面向量 与 的夹角为60°, , ,则 的值为( )A、 B、2 C、4 D、12. 如图所示, 是 的中线. 是 上的一点,且 ,若 ,其中 ,则 的值为( )
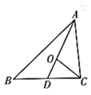 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 中, 点 在直线 上,且 ,则 等于 .14. 在 中,点 为 的外心, ,则 .15. 已知向量 , 是两个互相垂直的单位向量, 是坐标原点, , ,若 是直角三角形,则实数 的值为 .16. 已知a,b为单位向量,且a-b=0,若c=2a- b,则cos<a,c>=。
三、解答题
-
17. 设平面向量 , , .(1)、求 的值;(2)、若 ,求 的值.18. 在等边 中, ,点 为 的中点, 交 于点 .
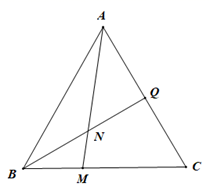 (1)、证明:点 为 的中点;(2)、若 ,求 的面积.19. 已知向量 , ,(1)、若 与 共线,求实数 ;(2)、求 的最小值及相应的 值.
(1)、证明:点 为 的中点;(2)、若 ,求 的面积.19. 已知向量 , ,(1)、若 与 共线,求实数 ;(2)、求 的最小值及相应的 值.