高中数学人教A版(2019)选择性必修二 第五章 一元函数的导数及其应用章末测验一
试卷日期:2022-03-22 考试类型:单元试卷
一、单选题
-
1. 下列各式正确的是( )A、 B、 C、 D、2. 已知是奇函数并且是上的单调函数,若方程有三个不同的实数解,则实数的取值范围为( )A、 B、 C、 D、3. 若函数 , 则是在有两个不同零点的( )A、充分不必要条件 B、必要不充分条件 C、充分且必要条件 D、既不充分也不必要条件4. 已知a,为正实数,直线与曲线相切,则的最小值是( )A、6 B、 C、8 D、5. 已知a>0,函数 , 若函数恰有两个零点,则实数a的取值范围是( )A、 B、 C、 D、6. 现有一球形气球,在吹气球时,气球的体积V(单位:L)与直径d(单位:)的关系式为 , 当时,气球体积的瞬时变化率为( )A、2π B、π C、 D、7. 定义在上的函数序列满足(为的导函数),且 , 都有 . 若存在 , 使得数列是首项和公比均为的等比数列,则下列关系式一定成立的是( ).A、 B、 C、 D、8. 已知 , 曲线在不同的三点 , , 处的切线均平行于x轴,则m的取值范围是( )A、 B、 C、 D、
二、多选题
-
9. 已如函数 , 则以下结论正确的是( )A、函数存在极大值和极小值 B、 C、函数存在最小值 D、对于任意实数k,方程最多有4个实数解10. 函数的图象如图所示,则下列结论正确的有( )
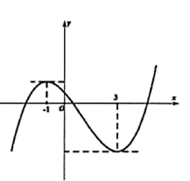 A、 B、 C、 D、11. 已知函数 , 则( )A、在上单调递减,在上单调递增 B、有2个不同的零点 C、若a, , 则 D、若且 , 则12. 函数 的定义域为 ,导函数 在 内的图象如图所示,则( )
A、 B、 C、 D、11. 已知函数 , 则( )A、在上单调递减,在上单调递增 B、有2个不同的零点 C、若a, , 则 D、若且 , 则12. 函数 的定义域为 ,导函数 在 内的图象如图所示,则( )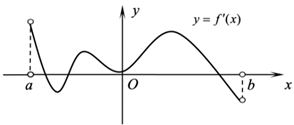 A、函数 在 内一定不存在最小值 B、函数 在 内只有一个极小值点 C、函数 在 内有两个极大值点 D、函数 在 内可能没有零点
A、函数 在 内一定不存在最小值 B、函数 在 内只有一个极小值点 C、函数 在 内有两个极大值点 D、函数 在 内可能没有零点三、填空题
-
13. 函数在点处的切线方程是.14. 对任意 , 若不等式恒成立,则实数a的最大值为 .15. 若函数恰有两个零点,则a的值为 .16. 已知函数 , 其中.若 , 则有个零点;若有两个零点,则实数的值构成的集合是.
四、解答题
-
17. 设实数 , 且 , 函数.(1)、求函数的单调区间;(2)、若函数有两个不同的零点.
(i)求的取值范围;
(ii)证明:.