江苏省无锡市惠山区2017年中考数学模拟试卷（4月份）

试卷日期：2017-11-27 考试类型：中考模拟

前去【出卷网】下载

一、选择题

  • 1. ﹣2的倒数是（   ）
    A、﹣ 12 B、12 C、﹣2 D、2

    查看试题解析

  • 2. 函数y= x−2 中自变量x的取值范围是（   ）
    A、x＞2 B、x≥2 C、x≤2 D、x≠2

    查看试题解析

  • 3. sin45°的值等于（   ）
    A、12 B、22 C、32 D、1

    查看试题解析

  • 4. 下列地方银行的标志中，既不是轴对称图形，也不是中心对称图形的是（   ）
    A、 B、 C、 D、

    查看试题解析

  • 5. 已知某圆锥的底面半径为3cm，母线长5cm，则它的侧面展开图的面积为（   ）
    A、30cm2 B、15cm2 C、30πcm2 D、15πcm2

    查看试题解析

  • 6. 六多边形的内角和为（   ）
    A、180° B、360° C、720° D、1080°

    查看试题解析

  • 7. 已知，AB是⊙O的弦，且OA=AB，则∠AOB的度数为（   ）
    A、30° B、45° C、60° D、90°

    查看试题解析

  • 8. 某区新教师招聘中，七位评委独立给出分数，得到一列数．若去掉一个最高分和一个最低分，得到一列新数，那么这两列数的相关统计量中，一定相等的是（   ）
    A、中位数 B、众数 C、方差 D、平均数

    查看试题解析

  • 9. 在△ABC中，AC=4，AB=5，则△ABC面积的最大值为（   ）
    A、6 B、10 C、12 D、20

    查看试题解析

  • 10. 直线l：y=mx﹣m+1（m为常数，且m≠0）与坐标轴交于A、B两点，若△AOB（O是原点）的面积恰为2，则符合要求的直线l有（   ）
    A、1条 B、2条 C、3条 D、4条

    查看试题解析

二、填空题

  • 11. 分解因式：xy﹣x=

    查看试题解析

  • 12. 去年无锡GDP（国民生产总值）总量实现约916 000 000 000元，该数据用科学记数法表示为元．

    查看试题解析

  • 13. 分式方程 4x = 2x+1 的解是 ．

    查看试题解析

  • 14. 若点A（1，m）在反比例函数y= 3x 的图象上，则m的值为 ．

    查看试题解析

  • 15. 写出命题“两直线平行，同位角相等”的结论部分： ．

    查看试题解析

  • 16. 如图，菱形ABCD中，对角线AC交BD于O，AB=8，E是CB的中点，则OE的长等于 ．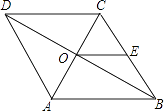

    查看试题解析

  • 17. 如图，∠A=110°，在边AN上取B，C，使AB=BC．点P为边AM上一点，将△APB沿PB折叠，使点A落在角内点E处，连接CE，则∠BPE+∠BCE=°．

    查看试题解析

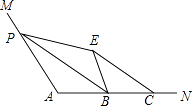  • 18. 已知，在平面直角坐标系中，点A（4，0），点B（m， 33 m），点C为线段OA上一点（点O为原点），则AB+BC的最小值为 ．

    查看试题解析

三、解答题

  • 19. 计算：计算与化简
    (1)、9 ﹣（﹣2）2+（﹣0.1）0；
    (2)、（x﹣2）2﹣（x+3）（x﹣1）．

    查看试题解析

  • 20. 计算：解不等式和方程组
    (1)、解不等式：5+x≥3（x﹣1）；
    (2)、解方程组： {x=3−y①2x+y=5② ．

    查看试题解析

  • 21. 已知，如图，等边△ABC中，点D为BC延长线上一点，点E为CA延长线上一点，且AE=DC，求证：AD=BE．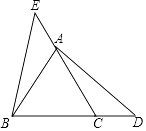


    查看试题解析

  • 22. 某校为迎接体育中考，了解学生的体育情况，学校随机调查了本校九年级50名学生“30秒跳绳”的次数，并将调查所得的数据整理如下：

    30秒跳绳次数的频数、频率分布表

    成绩段

    频数

    频率

    0≤x＜20

    5

    0.1

    20≤x＜40

    10

    a

    40≤x＜60

    b

    0.14

    60≤x＜80

    m

    c

    80≤x＜100

    12

    n

    根据以上图表信息，解答下列问题：

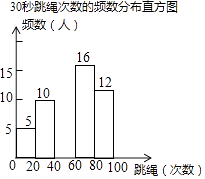    (1)、表中的a= ， m=；
    (2)、请把频数分布直方图补充完整；（画图后请标注相应的数据）
    (3)、若该校九年级共有600名学生，请你估计“30秒跳绳”的次数60次以上（含60次）的学生有多少人？

    查看试题解析

  • 23. 在2017年“KFC”篮球赛进校园活动中，某校甲、乙两队进行决赛，比赛规则规定：两队之间进行3局比赛，3局比赛必须全部打完，只要赢满2局的队为获胜队，假如甲、乙两队之间每局比赛输赢的机会相同，且乙队已经赢得了第1局比赛，那么甲队获胜的概率是多少？（请用“画树状图”或“列表”等方法写出分析过程）

    查看试题解析

  • 24. 已知，如图，线段AB，利用无刻度的直尺和圆规，作一个满足条件的△ABC：①△ABC为直角三角形；②tan∠A= 13 ．（注：不要求写作法，但保留作图痕迹）

    查看试题解析

  • 25. 在一张足够大的纸板上截取一个面积为3600平方厘米的矩形纸板ABCD，如图1，再在矩形纸板的四个角上切去边长相等的小正方形，再把它的边沿虚线折起，做成一个无盖的长方体纸盒，底面为矩形EFGH，如图2．设小正方形的边长为x厘米．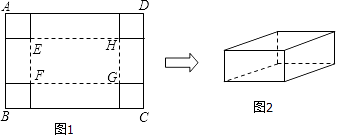

    (1)、当矩形纸板ABCD的一边长为90厘米时，求纸盒的侧面积的最大值；
    (2)、当EH：EF=7：2，且侧面积与底面积之比为9：7时，求x的值．

    查看试题解析

  • 26. 已知二次函数y=ax2﹣8ax（a＜0）的图象与x轴的正半轴交于点A，它的顶点为P．点C为y轴正半轴上一点，直线AC与该图象的另一交点为B，与过点P且垂直于x轴的直线交于点D，且CB：AB=1：7．

    (1)、求点A的坐标及点C的坐标（用含a的代数式表示）；
    (2)、连接BP，若△BDP与△AOC相似（点O为原点），求此二次函数的关系式．

    查看试题解析

  • 27. 如图，一次函数y=﹣ 12 x+m（m＞0）的图象与x轴、y轴分别交于点A，B，点C在线段OA上，点C的横坐标为n，点D在线段AB上，且AD=2BD，将△ACD绕点D旋转180°后得到△A1C1D．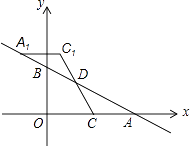

    (1)、若点C1恰好落在y轴上，试求 nm 的值；
    (2)、当n=4时，若△A1C1D被y轴分得两部分图形的面积比为3：5，求该一次函数的解析式．

    查看试题解析

  • 28. 阅读理解：小明热爱数学，在课外书上看到了一个有趣的定理﹣﹣“中线长定理”：三角形两边的平方和等于第三边的一半与第三边上的中线的平方和的两倍．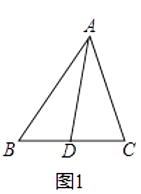
     
    如图1，在△ABC中，点D为BC的中点，根据“中线长定理”，可得：

    AB2+AC2=2AD2+2BD2 ． 小明尝试对它进行证明，部分过程如下：

    解：过点A作AE⊥BC于点E，如图2，在Rt△ABE中，AB2=AE2+BE2 ，

    同理可得：AC2=AE2+CE2 ， AD2=AE2+DE2 ，

    为证明的方便，不妨设BD=CD=x，DE=y，

    ∴AB2+AC2=AE2+BE2+AE2+CE2=…

    (1)、请你完成小明剩余的证明过程；
    (2)、理解运用：
    ①在△ABC中，点D为BC的中点，AB=6，AC=4，BC=8，则AD=；

    ②如图3，⊙O的半径为6，点A在圆内，且OA=2 2 ，点B和点C在⊙O上，且∠BAC=90°，点E、F分别为AO、BC的中点，则EF的长为


    (3)、拓展延伸：
    小明解决上述问题后，联想到《能力训练》上的题目：如图4，已知⊙O的半径为5 5 ，以A（﹣3，4）为直角顶点的△ABC的另两个顶点B，C都在⊙O上，D为BC的中点，求AD长的最大值．

    请你利用上面的方法和结论，求出AD长的最大值．

    查看试题解析