江苏省南京市溧水区2017年中考数学二模试卷

试卷日期：2017-11-27 考试类型：中考模拟

前去【出卷网】下载

一、选择题

1. 肥皂泡的泡壁厚度大约是0.000 07mm，用科学记数法表示为（）

A、7×10^﹣⁴ B、7×10^﹣⁵ C、0.7×10^﹣⁴ D、0.7×10^﹣⁵

查看试题解析
2. 下列计算正确的是（）

A、b⁵•b⁵=2b⁵ B、（aⁿ^﹣¹）³=a³ⁿ^﹣¹ C、a+2a²=3a³ D、（a﹣b）⁵（b﹣a）⁴=（a﹣b）⁹

查看试题解析
3. 数轴上的两个数﹣3与a，并且a＞﹣3，它们之间的距离可以表示为（）

A、3﹣a B、﹣3﹣a C、a﹣3 D、a+3

查看试题解析
4. 估计 $\frac{\sqrt{5} - 1}{2}$ 介于（）

A、0.6与0.7之间 B、0.7与0.8之间 C、0.8与0.9之间 D、0.9与1之间

查看试题解析
5. 如图所示，若干个全等的正五边形排成环状，要完成这一圆环共需要正五边形的个数为（）

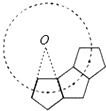A、10 B、9 C、8 D、7

查看试题解析
6. 如图，矩形ABCD中，AB=4，AD=7，其中点E为CD的中点．有一动点P，从点A按A→B→C→E的顺序在矩形ABCD的边上移动，移动到点E停止，在此过程中以点A，P，E三点为顶点的直角三角形的个数为（）

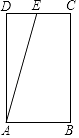A、2 B、3 C、4 D、5

查看试题解析

二、填空题

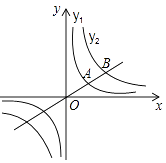
7. 5的算术平方根是；将 $\frac{1}{25}$ 写成负整数指数幂的形式是

查看试题解析
8. 计算 $\frac{\sqrt{3} - 3}{\sqrt{3}}$ 的结果是．

查看试题解析
9. 设x₁x₂是方程2x²+nx+m=0的两个根，且x₁+x₂=4，x₁x₂=3，则n= ．

查看试题解析
10. 在函数y= $\frac{x}{x + 1}$ 中，自变量x的取值范围是．

查看试题解析
11. 方程 $\frac{x - 2}{x}$ = $\frac{1}{3}$ 的解是．

查看试题解析
12. 已知（x﹣y﹣3）²+|x+y+2|=0，则x²﹣y²的值是．

查看试题解析
13. 若a^m=6，aⁿ=3，则a^m⁺²ⁿ的值为．

查看试题解析
14. 如图，过原点O的直线与反比例函数y₁、y₂的图象在第一象限内分别交于点A、B，且A为OB的中点．若点B的坐标为（8，2），则y₁与x的函数表达式是．

查看试题解析
15. 如图，在⊙O的内接五边形ABCDE中，∠B+∠E=215°，则∠CAD=°．

查看试题解析
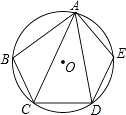16. 如图，四边形ABCD中，E、F、G、H依次是各边中点，O是四边形内一点，若S_四边形_AEOH=3，S_四边形_BFOE=4，S_四边形_CGOF=5，则S_四边形_DHOG= ．

查看试题解析

三、解答题

17. 解不等式组 ${\begin{matrix} 3 x + 1 \leq 2 (x + 1) \\ - x < 5 x + 12 \end{matrix}$ ，并写出它的整数解．

查看试题解析
18. 计算 $\frac{a}{a - 1}$ ﹣ $\frac{3 a - 1}{a^{2} - 1}$ ．

查看试题解析
19. 某校为更好的开展“冬季趣味运动会”活动，随机在各年级抽查了部分学生，了解他们最喜爱的趣味运动项目类型（跳长绳、踢毽子、背夹球、拔河共四类），并将统计结果绘制成如图不完整的频数分布表．
根据以上信息回答下列问题：
最喜爱的趣味运动项目类型频数分布表：
项目类型
频数
频率
跳长绳
25
a
踢毽子
20
0.2
背夹球
b
0.4
拔河
15
0.15

(1)、直接写出a= ， b=；

(2)、利用频数分布表中的数据，在图中绘制扇形统计图（注明项目、百分比、圆心角）；

(3)、若全校共有学生1200名，估计该校最喜爱背夹球和拔河的学生大约有多少人？

查看试题解析
20. 如图，在Rt△ABC中，∠BAC=90°，AD是BC边上的中线，过点D作BA的平行线交AC于点O，过点A作BC的平行线交DO的延长线于点E，连接CE．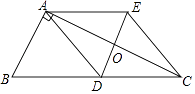

(1)、求证：四边形ADCE是菱形；

(2)、作出△ABC外接圆，不写作法，请指出圆心与半径；

(3)、若AO：BD= $\sqrt{3}$ ：2，求证：点E在△ABC的外接圆上．

查看试题解析
21. 综合题：求下列事件概率

(1)、小杨和小姜住在同一个小区，该小区到苏果超市有A、B、C三条路线．
①求小杨随机选择一条路线，恰好是A路线的概率；
②求小杨和小姜两人分别随机选择一条路线去苏果超市，恰好两人选择同一条路线的概率．

(2)、有4位顾客在超市中选购4种品牌的方便面．如果每位顾客从4种品牌中随机的选购一种，那么4位顾客选购同一品牌的概率是，至少有2位顾客选择的不是同一品牌的概率是（直接填字母序号）
A． $\frac{1}{4}$ B．（ $\frac{1}{4}$ ）³ C.1﹣（ $\frac{1}{4}$ ）³ D.1﹣（ $\frac{3}{4}$ ）³ ．

查看试题解析
22. 如图，四边形ABCD内接于⊙O，BD是⊙O的直径，AE⊥CD于点E，DA平分∠BDE．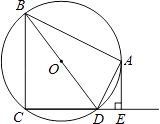

(1)、求证：AE是⊙O的切线；

(2)、如果AB=4，AE=2，求⊙O的半径．

查看试题解析
23. 新房装修后，甲居民购买家居用品的清单如下表，因污水导致部分信息无法识别，根据下表解决问题：
家居用品名称
单价（元）
数量（个）
金额（元）
挂钟
30
2
60
垃圾桶
15

塑料鞋架
40

艺术字画
a
2
90
电热水壶
35
1
b
合计
8
280

(1)、直接写出a= ， b=；

(2)、甲居民购买了垃圾桶，塑料鞋架各几个？

(3)、若甲居民再次购买艺术字画和垃圾桶两种家居用品，共花费150元，则有哪几种不同的购买方案？

查看试题解析
24. 某种事物经历了加热，冷却两个联系过程，折线图DEF表示食物的温度y（℃）与时间x（s）之间的函数关系（0≤x≤160），已知线段EF表示的函数关系中，时间每增加1s，食物温度下降0.3℃，根据图象解答下列问题；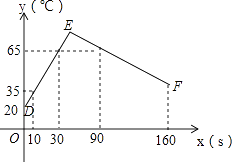

(1)、当时间为20s、100s时，该食物的温度分别为℃，℃；

(2)、求线段DE所表示的y与x之间的函数表达式；

(3)、时间是多少时，该食物的温度最高？最高是多少？

查看试题解析
25. 如图，为了测出某塔CD的高度，在塔前的平地上选择一点A，用测角仪测得塔顶D的仰角为30°，在A、C之间选择一点B（A、B、C三点在同一直线上）．用测角仪测得塔顶D的仰角为75°，且AB间的距离为40m．

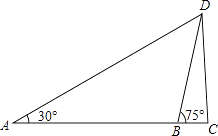(1)、求点B到AD的距离；

(2)、求塔高CD（结果用根号表示）．

查看试题解析
26. 已知二次函数y₁=a（x﹣2）²+k中，函数y₁与自变量x的部分对应值如表：
x
…
1
2
3
4
…
y
…
2
1
2
5
…

(1)、求该二次函数的表达式；

(2)、将该函数的图象向左平移2个单位长度，得到二次函数y₂的图象，分别在y₁、y₂的图象上取点A（m，n₁）B（m+1，n₂），试比较n₁与n₂的大小．

查看试题解析
27. 【问题探究】
已知：如图①所示，∠MPN的顶点为P，⊙O的圆心O从顶点P出发，沿着PN方向平移．

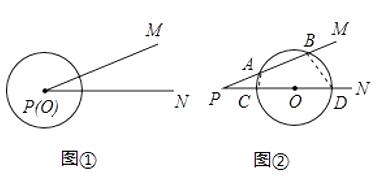(1)、如图②所示，当⊙O分别与射线PM，PN相交于A、B、C、D四个点，连接AC、BD，可以证得△PAC∽△ ，从而可以得到：PA•P B=P C•P D．

(2)、如图③所示，当⊙O与射线PM相切于点A，与射线PN相交于C、D两个点．求证：PA²=PC•PD．

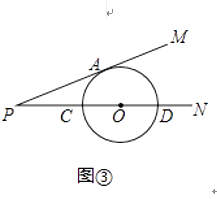(3)、【简单应用】
如图④所示，（2）中条件不变，经过点P的另一条射线与⊙O相交于E、F两点．利用上述（1），（2）两问的结论，直接写出线段PA与PE、PF之间的数量关系；当PA=4 $\sqrt{3}$ ，E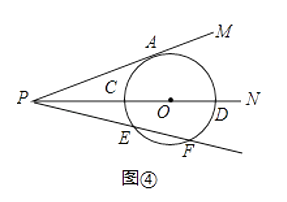F=2，则PE= ．

(4)、【拓展延伸】如图⑤所示，在以O为圆心的两个同心圆中，A、B是大⊙O上的任意两点，经过A、B 两点作线段，分别交小⊙O于C、E、D、F四个点．求证：AC•AE=BD•BF．（友情提醒：可直接运用本题上面所得到的相关结论）

查看试题解析

项目类型	频数	频率
跳长绳	25	a
踢毽子	20	0.2
背夹球	b	0.4
拔河	15	0.15

家居用品名称	单价（元）	数量（个）	金额（元）
挂钟	30	2	60
垃圾桶	15
塑料鞋架	40
艺术字画	a	2	90
电热水壶	35	1	b
合计		8	280

x	…	1	2	3	4	…
y	…	2	1	2	5	…