江苏省连云港市2017年中考数学模拟试卷
试卷日期:2017-11-27 考试类型:中考模拟
一、选择题
-
1. 下列事件中最适合使用普查方式收集数据的是( )
A、了解某班同学的身高情况 B、了解全市每天丢弃的废旧电池数 C、了解50发炮弹的杀伤半径 D、了解我省农民的年人均收入情况2. 下列水平放置的四个几何体中,主视图与其它三个不相同的是( )A、 B、
B、 C、
C、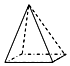 D、
D、 3. 下列函数中,自变量x的取值范围是x>3的是( )A、y=x﹣3 B、 C、 D、y=4. 已知反比例函数y=﹣ , 下列结论不正确的是( )A、图象必经过点(﹣1,3) B、若x>1,则﹣3<y<0 C、图象在第二、四象限内 D、y随x的增大而增大5. 下列各式结果是负数的是( )A、﹣(﹣3) B、﹣|﹣3| C、3﹣2 D、(﹣3)26. 如图,在平面直角坐标系中,菱形OACB的顶点O在原点,点C的坐标为(4,0),点B的纵坐标是﹣1,则顶点A坐标是( )
3. 下列函数中,自变量x的取值范围是x>3的是( )A、y=x﹣3 B、 C、 D、y=4. 已知反比例函数y=﹣ , 下列结论不正确的是( )A、图象必经过点(﹣1,3) B、若x>1,则﹣3<y<0 C、图象在第二、四象限内 D、y随x的增大而增大5. 下列各式结果是负数的是( )A、﹣(﹣3) B、﹣|﹣3| C、3﹣2 D、(﹣3)26. 如图,在平面直角坐标系中,菱形OACB的顶点O在原点,点C的坐标为(4,0),点B的纵坐标是﹣1,则顶点A坐标是( )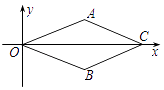 A、(2,1) B、(1,﹣2) C、(1,2) D、(2,﹣1)7.
A、(2,1) B、(1,﹣2) C、(1,2) D、(2,﹣1)7.已知一次函数y=kx+b的图象如图,则关于x的不等式k(x﹣4)﹣2b>0的解集为( )
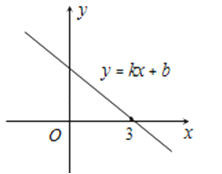 A、x>﹣2 B、x<﹣2 C、x>2 D、x<38. 在△ABC中,AB=3,AC= .当∠B最大时,BC的长是( )A、 B、 C、 D、2
A、x>﹣2 B、x<﹣2 C、x>2 D、x<38. 在△ABC中,AB=3,AC= .当∠B最大时,BC的长是( )A、 B、 C、 D、2二、填空题
-
9. 的倒数为 .10. 我国的南海资源丰富,其面积为3500000平方千米,相当于渤海、黄海和东海总面积的3倍.其中3500000用科学记数法可表示为 .11. 如果实数x、y满足方程组 ,那么x2﹣y2= .12. 某药品原价每盒25元,为了响应国家解决老百姓看病贵的号召,经过连续两次降价,现在售价每盒16元,则该药品平均每次降价的百分率是 .13. 口袋内装有一些除颜色外完全相同的红球、白球和黑球,从中摸出一球,摸出红球的概率是0.2,摸出白球的概率是0.5,那么摸出黑球的概率是 .
14. 若正多边形的一个内角等于140°,则这个正多边形的边数是 .15. 如图,⊙O的半径是4,△ABC是⊙O的内接三角形,过圆心O分别作AB,BC,AC的垂线,垂足为E,F,G,连接EF.若OG﹦1,则EF为 . 16. 在△ABC中,AB=AC,CD=CB,若∠ACD=42°,则∠BAC=°.
16. 在△ABC中,AB=AC,CD=CB,若∠ACD=42°,则∠BAC=°. 17. 如图,一段抛物线y=﹣x(x﹣3)(0≤x≤3),记为C1 , 它与x轴交于点O,A1;将C1绕点A1旋转180°得C2 , 交x 轴于点A2;将C2绕点A2旋转180°得C3 , 交x 轴于点A3;…如此进行下去,得到一条“波浪线”.若点P(37,m)在此“波浪线”上,则m的值为 .
17. 如图,一段抛物线y=﹣x(x﹣3)(0≤x≤3),记为C1 , 它与x轴交于点O,A1;将C1绕点A1旋转180°得C2 , 交x 轴于点A2;将C2绕点A2旋转180°得C3 , 交x 轴于点A3;…如此进行下去,得到一条“波浪线”.若点P(37,m)在此“波浪线”上,则m的值为 .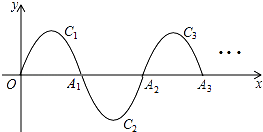 18. 如图,矩形ABCD被分成四部分,其中△ABE、△ECF、△ADF的面积分别为2、3、4,则△AEF的面积为 .
18. 如图,矩形ABCD被分成四部分,其中△ABE、△ECF、△ADF的面积分别为2、3、4,则△AEF的面积为 .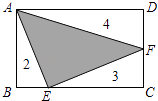
三、解答题
-
19. 计算题:计算题
(1)、计算:(2)、解不等式: .20. 先化简再求值: ,其中x是方程x2=2x的根.21. 某中学初三(1)班共有40名同学,在一次30秒跳绳测试中他们的成绩统计如下表:跳绳数/个
81
85
90
93
95
98
100
人 数
1
2
8
11
5
将这些数据按组距5(个)分组,绘制成如图的频数分布直方图(不完整).
 (1)、将表中空缺的数据填写完整,并补全频数分布直方图;(2)、这个班同学这次跳绳成绩的众数是个,中位数是个;(3)、若跳满90个可得满分,学校初三年级共有720人,试估计该中学初三年级还有多少人跳绳不能得满分.
(1)、将表中空缺的数据填写完整,并补全频数分布直方图;(2)、这个班同学这次跳绳成绩的众数是个,中位数是个;(3)、若跳满90个可得满分,学校初三年级共有720人,试估计该中学初三年级还有多少人跳绳不能得满分.
22. 甲、乙、丙、丁四位同学进行一次羽毛球单打比赛,要从中选出两位同学打第一场比赛.请用树状图法或列表法,求恰好选中甲、乙两位同学的概率.23. 分如图,在▱ABCD中,点E、F分别是AD、BC的中点,分别连接BE、DF、BD.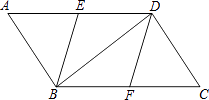 (1)、求证:△AEB≌△CFD;(2)、若四边形EBFD是菱形,求∠ABD的度数.24. 为了提高产品的附加值,某公司计划将研发生产的1200件新产品进行精加工后再投放市场.现有甲、乙两个工厂都具备加工能力,公司派出相关人员分别到这两间工厂了解情况,获得如下信息:
(1)、求证:△AEB≌△CFD;(2)、若四边形EBFD是菱形,求∠ABD的度数.24. 为了提高产品的附加值,某公司计划将研发生产的1200件新产品进行精加工后再投放市场.现有甲、乙两个工厂都具备加工能力,公司派出相关人员分别到这两间工厂了解情况,获得如下信息:信息一:甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天;
信息二:乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍.
根据以上信息,求甲、乙两个工厂每天分别能加工多少件新产品?
25. 如图所示,把一张长方形卡片ABCD放在每格宽度为12mm的横格纸中,恰好四个顶点都在横格线上,已知∠α=36°,求长方形卡片的周长.(精确到1mm)(参考数据:sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)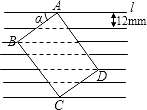 26. 如图,点E是边长为1的正方形ABCD的边AB上任意一点(不含A,B),过B,C,E三点的圆与BD相交于点F,与CD相交于点G,与∠ABC的外角平分线相交于点H.
26. 如图,点E是边长为1的正方形ABCD的边AB上任意一点(不含A,B),过B,C,E三点的圆与BD相交于点F,与CD相交于点G,与∠ABC的外角平分线相交于点H.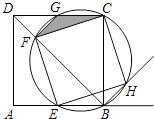 (1)、求证:四边形EFCH是正方形;
(1)、求证:四边形EFCH是正方形;
(2)、设BE=x,△CFG的面积为y,求y与x的函数关系式,并求y的最大值.27. 已知:点E为AB边上的一个动点.(1)、如图1,若△ABC是等边三角形,以CE为边在BC的同侧作等边△DEC,连结AD.试比较∠DAC与∠B的大小,并说明理由;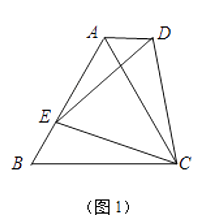 (2)、如图2,若△ABC中,AB=AC,以CE为底边在BC的同侧作等腰△DEC,且△DEC∽△ABC,连结AD.试判断AD与BC的位置关系,并说明理由;
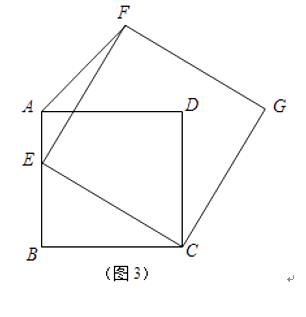
(2)、如图2,若△ABC中,AB=AC,以CE为底边在BC的同侧作等腰△DEC,且△DEC∽△ABC,连结AD.试判断AD与BC的位置关系,并说明理由; (3)、如图3,若四边形ABCD是边长为2的正方形,以CE为边在BC的同侧作正方形ECGF.
(3)、如图3,若四边形ABCD是边长为2的正方形,以CE为边在BC的同侧作正方形ECGF.①试说明点G一定在AD的延长线上;
②当点E在AB边上由点B运动至点A时,点F随之运动,求点F的运动路径长.
 28. 在平面直角坐标系xOy中,抛物线y=ax2+bx+4经过A(﹣3,0)、B(4,0)两点,且与y轴交于点C,点D在x轴的负半轴上,且BD=BC,有一动点P从点A出发,沿线段AB以每秒1个单位长度的速度向点B移动,同时另一个动点Q从点C出发,沿线段CA以某一速度向点A移动.
28. 在平面直角坐标系xOy中,抛物线y=ax2+bx+4经过A(﹣3,0)、B(4,0)两点,且与y轴交于点C,点D在x轴的负半轴上,且BD=BC,有一动点P从点A出发,沿线段AB以每秒1个单位长度的速度向点B移动,同时另一个动点Q从点C出发,沿线段CA以某一速度向点A移动. (1)、求该抛物线的解析式;(2)、若经过t秒的移动,线段PQ被CD垂直平分,求此时t的值;(3)、该抛物线的对称轴上是否存在一点M,使MQ+MA的值最小?若存在,求出点M的坐标;若不存在,请说明理由.
(1)、求该抛物线的解析式;(2)、若经过t秒的移动,线段PQ被CD垂直平分,求此时t的值;(3)、该抛物线的对称轴上是否存在一点M,使MQ+MA的值最小?若存在,求出点M的坐标;若不存在,请说明理由.