湖南省岳阳市2017年中考数学二模试卷
试卷日期:2017-11-27 考试类型:中考模拟
一、选择题
-
1. 实数a,b,c,d在数轴上的对应点的位置如图所示,这四个数中,绝对值最大的是( )
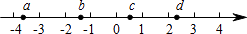 A、a B、b C、c D、d2. 下列四个圆形图案中,分别以它们所在圆的圆心为旋转中心,顺时针旋转120°后,能与原图形完全重合的是( )A、
A、a B、b C、c D、d2. 下列四个圆形图案中,分别以它们所在圆的圆心为旋转中心,顺时针旋转120°后,能与原图形完全重合的是( )A、 B、
B、 C、
C、 D、
D、 3. 下列计算正确的是( )A、 + = B、(ab3)2=a2b5 C、2a+3a=6a D、a•a3=a44. 某市6月份日平均气温统计如图所示,则在日平均气温这组数据中,众数和中位数分别是( )
3. 下列计算正确的是( )A、 + = B、(ab3)2=a2b5 C、2a+3a=6a D、a•a3=a44. 某市6月份日平均气温统计如图所示,则在日平均气温这组数据中,众数和中位数分别是( )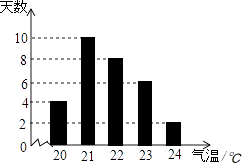 A、21,21 B、21,21.5 C、21,22 D、22,225. 如图,若平行四边形ABCD中,AB=6,AD=4,∠B=150°,则平行四边形ABCD的面积为( )
A、21,21 B、21,21.5 C、21,22 D、22,225. 如图,若平行四边形ABCD中,AB=6,AD=4,∠B=150°,则平行四边形ABCD的面积为( )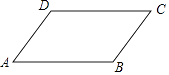 A、6 B、12 C、12 D、246. 已知关于x的一元二次方程mx2+2x﹣1=0有两个不相等的实数根,则m的取值范围是( )A、m<﹣1 B、m>1 C、m<1且m≠0 D、m>﹣1且m≠07. 在六张卡片上分别写有 ,π,1.5,5,0, 六个数,从中任意抽取一张,卡片上的数为无理数的概率是( )A、 B、 C、 D、8. 如图,过半径为6的圆O上一点A作圆O的切线l,P为圆O的一个动点,作PH⊥l于点H,连接PA.如果PA=x,AH=y,那么下列图象中,能大致表示y与x的函数关系的是( )
A、6 B、12 C、12 D、246. 已知关于x的一元二次方程mx2+2x﹣1=0有两个不相等的实数根,则m的取值范围是( )A、m<﹣1 B、m>1 C、m<1且m≠0 D、m>﹣1且m≠07. 在六张卡片上分别写有 ,π,1.5,5,0, 六个数,从中任意抽取一张,卡片上的数为无理数的概率是( )A、 B、 C、 D、8. 如图,过半径为6的圆O上一点A作圆O的切线l,P为圆O的一个动点,作PH⊥l于点H,连接PA.如果PA=x,AH=y,那么下列图象中,能大致表示y与x的函数关系的是( )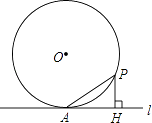 A、
A、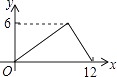 B、
B、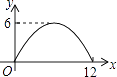 C、
C、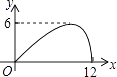 D、
D、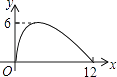
二、填空题
-
9. 已知∠A=47°,则∠A的余角等于度.10. 使代数式 有意义的x的取值范围是 .
11. 如图,点P为∠AOB平分线上的一点,PC⊥OB于点C,且PC=4,点P到OA的距离为 .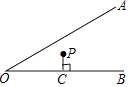 12. 计算: = .13. 2017年岳阳教育将完成实事攻坚任务,实施薄改工程,利用中央和地方专项资金9.4亿元,改造薄弱学校800所,9.4亿元用科学记数法表示为元.14. 甲乙两人进行飞镖比赛,每人各投5次,其中甲所得环数的方差为15,乙所得环数的方差为12.5,那么成绩较稳定的是(填“甲”或“乙”).15. 如图所示,圆内接四边形ABCD两组对边的延长线分别相交于点E,F,且∠A=56°,∠E=32°,则∠F= .
12. 计算: = .13. 2017年岳阳教育将完成实事攻坚任务,实施薄改工程,利用中央和地方专项资金9.4亿元,改造薄弱学校800所,9.4亿元用科学记数法表示为元.14. 甲乙两人进行飞镖比赛,每人各投5次,其中甲所得环数的方差为15,乙所得环数的方差为12.5,那么成绩较稳定的是(填“甲”或“乙”).15. 如图所示,圆内接四边形ABCD两组对边的延长线分别相交于点E,F,且∠A=56°,∠E=32°,则∠F= . 16. 在平面直角坐标系xOy中,正方形A1B1C1O、A2B2C2B1、A3B3C3B2 , …,按图所示的方式放置.点A1、A2、A3 , …和点B1、B2、B3 , …分别在直线y=kx+b和x轴上.已知C1(1,﹣1),C2( , ),则点A3的坐标是 .
16. 在平面直角坐标系xOy中,正方形A1B1C1O、A2B2C2B1、A3B3C3B2 , …,按图所示的方式放置.点A1、A2、A3 , …和点B1、B2、B3 , …分别在直线y=kx+b和x轴上.已知C1(1,﹣1),C2( , ),则点A3的坐标是 .
三、解答题
-
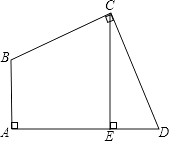
17. 计算:( )﹣1﹣2cos30°+ +(2017﹣π)0 .18. 已知x2﹣3x+2=0,求代数式(x﹣1)(3x+1)﹣(x+2)2+5的值.19. 如图,四边形ABCD中,∠A=∠BCD=90°,BC=CD,CE⊥AD,垂足为E,求证:AE=CE.
 20. 保障房建设是民心工程,某市从2012年开始加快保障房建设进程,现统计了该市2012年到2016年5月新建保障房情况,绘制成如图所示的折线统计图和不完整的条形统计图.
20. 保障房建设是民心工程,某市从2012年开始加快保障房建设进程,现统计了该市2012年到2016年5月新建保障房情况,绘制成如图所示的折线统计图和不完整的条形统计图.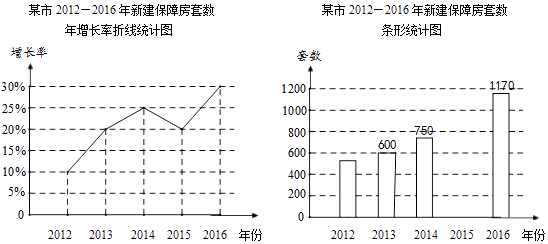 (1)、小丽看了统计图后说:“该市2015年新建保障房的套数比2014年少了.”你认为小丽说法正确吗?请说明理由;
(1)、小丽看了统计图后说:“该市2015年新建保障房的套数比2014年少了.”你认为小丽说法正确吗?请说明理由;
(2)、求补全条形统计图;(3)、求这5年平均每年新建保障房的套数.21. 如图所示,等边三角形ABC放置在平面直角坐标系中,已知A(0,0)、B(6,0),反比例函数的图象经过点C.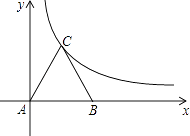 (1)、求点C的坐标及反比例函数的解析式.(2)、将等边△ABC向上平移n个单位,使点B恰好落在双曲线上,求n的值.22. 2015年某企业按餐厨垃圾处理费50元/吨、建筑垃圾处理费20元/吨的收费标准,共支付餐厨和建筑垃圾处理费7000元.从2016年元月起,收费标准上调为:餐厨垃圾处理费120元/吨,建筑垃圾处理费40元/吨.若该企业2016年处理的这两种垃圾数量与2015年相比没有变化,就要多支付垃圾处理费8600元.(1)、该企业2015年处理的餐厨垃圾和建筑垃圾各多少吨?(2)、该企业计划2016年将上述两种垃圾处理总量减少到200吨,且建筑垃圾处理量不超过餐厨垃圾处理量的3倍,则2016年该企业最少需要支付这两种垃圾处理费共多少元?23. 在△ABC中,CA=CB,在△AED中,DA=DE,点D,E分别在CA,AB上.(1)、如图①,若∠ACB=∠ADE=90°,则CD与BE的数量关系是;
(1)、求点C的坐标及反比例函数的解析式.(2)、将等边△ABC向上平移n个单位,使点B恰好落在双曲线上,求n的值.22. 2015年某企业按餐厨垃圾处理费50元/吨、建筑垃圾处理费20元/吨的收费标准,共支付餐厨和建筑垃圾处理费7000元.从2016年元月起,收费标准上调为:餐厨垃圾处理费120元/吨,建筑垃圾处理费40元/吨.若该企业2016年处理的这两种垃圾数量与2015年相比没有变化,就要多支付垃圾处理费8600元.(1)、该企业2015年处理的餐厨垃圾和建筑垃圾各多少吨?(2)、该企业计划2016年将上述两种垃圾处理总量减少到200吨,且建筑垃圾处理量不超过餐厨垃圾处理量的3倍,则2016年该企业最少需要支付这两种垃圾处理费共多少元?23. 在△ABC中,CA=CB,在△AED中,DA=DE,点D,E分别在CA,AB上.(1)、如图①,若∠ACB=∠ADE=90°,则CD与BE的数量关系是;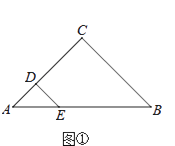 (2)、若∠ACB=∠ADE=120°,将△AED绕点A旋转至如图②所示的位置,则CD与BE的数量关系是;,
(2)、若∠ACB=∠ADE=120°,将△AED绕点A旋转至如图②所示的位置,则CD与BE的数量关系是;,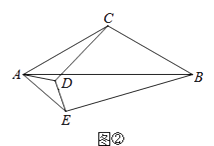 (3)、若∠ACB=∠ADE=2α(0°<α<90°),将△AED绕点A旋转至如图③所示的位置,探究线段CD与BE的数量关系,并加以证明(用含α的式子表示).
(3)、若∠ACB=∠ADE=2α(0°<α<90°),将△AED绕点A旋转至如图③所示的位置,探究线段CD与BE的数量关系,并加以证明(用含α的式子表示). 24. 如图,在平面直角坐标系中,抛物线y=ax2+bx﹣3(a≠0)与x轴交于点A(﹣2,0)、B(4,0)两点,与y轴交于点C.
24. 如图,在平面直角坐标系中,抛物线y=ax2+bx﹣3(a≠0)与x轴交于点A(﹣2,0)、B(4,0)两点,与y轴交于点C.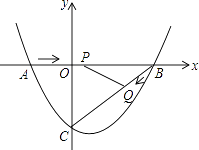 (1)、求抛物线的解析式;(2)、点P从A点出发,在线段AB上以每秒3个单位长度的速度向B点运动,同时点Q从B点出发,在线段BC上以每秒1个单位长度的速度向C点运动,其中一个点到达终点时,另一个点也停止运动,当△PBQ存在时,求运动多少秒使△PBQ的面积最大,最大面积是多少?(3)、当△PBQ的面积最大时,在BC下方的抛物线上存在点K,使S△CBK:S△PBQ=5:2,求K点坐标.
(1)、求抛物线的解析式;(2)、点P从A点出发,在线段AB上以每秒3个单位长度的速度向B点运动,同时点Q从B点出发,在线段BC上以每秒1个单位长度的速度向C点运动,其中一个点到达终点时,另一个点也停止运动,当△PBQ存在时,求运动多少秒使△PBQ的面积最大,最大面积是多少?(3)、当△PBQ的面积最大时,在BC下方的抛物线上存在点K,使S△CBK:S△PBQ=5:2,求K点坐标.