河北省张家口市2016-2017学年高一下学期数学期末考试试卷

试卷日期：2017-11-23 考试类型：期末考试

前去【出卷网】下载

一、选择题

1. 若实数a，b∈R且a＞b，则下列不等式恒成立的是（）

A、a²＞b² B、 $\frac{a}{b} > 1$ C、2^a＞2^b D、lg（a﹣b）＞0

查看试题解析
2. 如果ac＜0，bc＜0，那么直线ax+by+c=0不通过（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 已知数列{a_n}为等差数列，且a₂+a₃+a₁₀+a₁₁=48，则a₆+a₇=（）

A、21 B、22 C、23 D、24

查看试题解析
4. 已知x＞3，则对于函数f（x）=x+ $\frac{4}{x - 3}$ ，下列说法正确的是（）

A、函数f（x）有最大值7 B、函数f（x）有最小值7 C、函数f（x）有最小值4 D、函数f（x）有最大值4

查看试题解析
5. 在△ABC中，内角A，B，C的对边分别为a，b，c且a²=b²+c²+bc，则A=（）

A、 $\frac{2 π}{3}$ B、 $\frac{5 π}{6}$ C、 $\frac{π}{6}$ D、 $\frac{π}{3}$

查看试题解析
6. 已知点（x₀ ， y₀）在x²+y²=r²（r＞0）外，则直线x₀x+y₀y=r²与圆x²+y²=r²的位置关系为（）

A、相交 B、相切 C、相离 D、相交、相切、相离三种情况均有可能

查看试题解析
7. α，β为两个不同的平面，m，n为两条不同的直线，下列命题中正确的是（）
①若α∥β，m⊂α，则m∥β；
②若m∥α，n⊂α，则m∥n；
③若α⊥β，α∩β=n，m⊥n，则m⊥β；
④若n⊥α，n⊥β，m⊥α，则m⊥β．

A、①③ B、①④ C、②③ D、②④

查看试题解析
8. 四棱锥S﹣ABCD的底面ABCD是正方形，各侧棱长与底面的边长均相等，M为SA的中点，则直线BM与SC所成的角的余弦值为（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{6}}{3}$ C、 $\frac{\sqrt{3}}{3}$ D、 $\frac{\sqrt{2}}{4}$

查看试题解析
9. 已知实数x，y满足 ${\begin{matrix} 2 x + y \leq 2 \\ x \geq 0 \\ x + y \geq 0 \end{matrix}$ ，z=（x+1）²+（y+2）² ，则z的最小值为（）

A、 $\frac{3 \sqrt{2}}{2}$ B、 $\frac{9}{2}$ C、 $\sqrt{5}$ D、5

查看试题解析
10. 设等差数列{a_n}的前n项和为S_n ，若S₇=21，S₁₇=34，则S₂₇=（）

A、27 B、﹣27 C、0 D、37

查看试题解析
11. 一个几何体的三视图如图所示，已知这个几何体的体积为 $10 \sqrt{3}$ ，则这个几何体的外接球的表面积为（）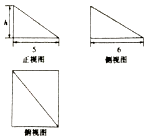

A、8π B、24π C、48π D、64π

查看试题解析
12. 平面α内有一以AB为直径的圆，PA⊥α，点C在圆周上移动（不与A，B重合），点D，E分别是A在PC，PB上的射影，则（）

A、∠ACD是二面角A﹣PC﹣B的平面角 B、∠AED是二面角A﹣PB﹣C的平面角 C、∠EDA是二面角A﹣PC﹣B的平面角 D、∠DAE是二面角B﹣PA﹣C的平面角

查看试题解析

二、填空题

13. 已知等比数列{a_n}的首项为32，公比为﹣ $\frac{1}{2}$ ，则等比数列{a_n}的前5项和为．

查看试题解析
14. 若直线l₁：（a+2）x+（a﹣1）y+8=0与直线l₂：（a﹣3）x+（a+2）y﹣7=0垂直，那么a的值为．

查看试题解析
15. 已知三棱柱ABC﹣A₁B₁C₁中，底面△ABC为等边三角形，AA₁⊥平面ABC，AB=4，AA₁=6．点E，F分别是棱BB₁ ， CC₁上的点，则三棱锥A﹣A₁EF的体积为．

查看试题解析
16. 甲、乙两位打字员在两台电脑上各自输入A，B两种类型的文件的部分文字才能使这两类文件成为成品．已知A文件需要甲输入0.5小时，乙输入0.2小时；B文件需要甲输入0.3小时，乙输入0.6小时．在一个工作日中，甲至多只能输入6小时，乙至多只能输入8小时，A文件每份的利润为60元，B文件每份的利润为80元，则甲、乙两位打字员在一个工作日内获得的最大利润是元．

查看试题解析

三、解答题

17. 如图所示，三棱锥V﹣ABC中，VA=VB=AC=BC=2，AB=2 $\sqrt{3}$ ，VC=1，线段AB的中点为D．

(1)、求证：平面VCD⊥平面ABC；

(2)、求三棱锥V﹣ABC的体积．

查看试题解析
18. 已知数列{a_n}的首项a₁=1，前n项和为S_n ，且满足（n+1）a_n=2S_n（n∈N^*）．

(1)、求数列{a_n}的通项公式；

(2)、设b_n=a_ncos（πa_n），求数列{b_n）的前n项和T_n ．

查看试题解析
19. 设△ABC的内角A，B，C所对的边分别为a，b，c且acosB=4，bsinA=3．

(1)、求tanB及边长a的值；

(2)、若△ABC的面积S=9，求△ABC的周长．

查看试题解析
20. 已知a∈R，解关于x的不等式（a﹣1）x²+（2a+3）x+a+2＜0．

查看试题解析
21. 已知点H（x₀ ， y₀）在圆C：x²+y²+Dx+Ey+F=0（其中点C为圆心，D²+E²﹣4F＞0）外，由点H向圆C引切线，其中一个切点为M．
求证：|HM|= $\sqrt{x_{0}^{2} + y_{0}^{2} + D x_{0} + E y_{0} + F}$ ；

(1)、已知点H（x₀ ， y₀）在圆C：x²+y²+Dx+Ey+F=0（其中点C为圆心，D²+E²﹣4F＞0）外，由点H向圆C引切线，其中一个切点为M．
求证：|HM|= $\sqrt{x_{0}^{2} + y_{0}^{2} + D x_{0} + E y_{0} + F}$ ；

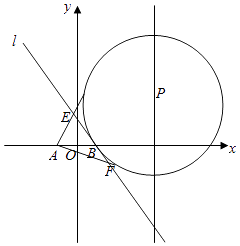
(2)、如图，P是直线x=4上一动点，以P为圆心的圆P经定点B（1，0），直线l是圆P在点B处的切线，过A（﹣1，0）作圆P的两条切线分别与l交于E，F两点．
求证：|EA|+|EB|为定值．

查看试题解析
22. 已知长方体ABCD﹣A₁B₁C₁D₁中，底面ABCD为正方形，DD₁⊥平面ABCD，AB=4，AA₁=2，点E₁在棱C₁D₁上，且D₁E₁=3．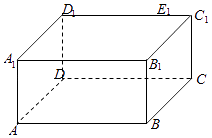
（Ⅰ）在棱CD上确定一点E，使得直线EE₁∥平面D₁DB，并写出证明过程；
（Ⅱ）若动点F在正方形ABCD内，且AF=2，请说明点F的轨迹，探求E₁F长度的最小值并求此时直线E₁F与平面ABCD所成角的正弦值．

查看试题解析