河北省廊坊市省级示范高中联合体2016-2017学年高一下学期数学期末考试试卷

试卷日期：2017-11-23 考试类型：期末考试

前去【出卷网】下载

一、选择题

1. 数列{a_n}的前几项为 $\frac{1}{2} ， 3 ， \frac{11}{2} ， 8 ， \frac{21}{2} \dots$ ，则此数列的通项可能是（）

A、 $a_{n} = \frac{5 n - 4}{2}$ B、 $a_{n} = \frac{3 n - 2}{2}$ C、 $a_{n} = \frac{6 n - 5}{2}$ D、 $a_{n} = \frac{10 n - 9}{2}$

查看试题解析
2. 对于任意实数a、b、c、d，下列命题中，真命题为（）
①若a＞b，c≠0，则ac＞bc；
②若a＞b，则ac²＞bc²；
③若ac²＞bc² ，则a＞b；
④若a＞b，则 $\frac{1}{a}$ ＜ $\frac{1}{b}$ ．

A、① B、② C、③ D、④

查看试题解析
3. 在空间直角坐标系中点P（1，3，﹣5）关于xOy对称的点的坐标是（　　）

A、（﹣1，3，﹣5） B、（1，﹣3，5） C、（1，3，5） D、（﹣1，﹣3，5）

查看试题解析
4. 直线mx+ $\frac{n}{2}$ y﹣1=0在y轴上的截距是﹣1，且它的倾斜角是直线 $\sqrt{3} x - y - 3 \sqrt{3}$ =0的倾斜角的2倍，则（）

A、m=﹣ $\sqrt{3}$ ，n=﹣2 B、m= $\sqrt{3}$ ，n=2 C、m= $\sqrt{3}$ ，n=﹣2 D、m=﹣ $\sqrt{3}$ ，n=2

查看试题解析
5. 圆心为（0，1）且与直线y=2相切的圆的方程为（）

A、（x﹣1）²+y²=1 B、（x+1）²+y²=1 C、x²+（y﹣1）²=1 D、x²+（y+1）²=1

查看试题解析
6. 已知等比数列{a_n}中，各项都是正数，且a₁ ， $\frac{1}{2}$ a₃ ， 2a₂成等差数列，则 $\frac{a_{9} + a_{10}}{a_{7} + a_{8}}$ =（　　）

A、1+ $\sqrt{2}$ B、1﹣ $\sqrt{2}$ C、3+2 $\sqrt{2}$ D、3﹣2 $\sqrt{2}$

查看试题解析
7. 关于x的不等式ax²+bx+2＞0的解集为（﹣1，2），则关于x的不等式bx²﹣ax﹣2＞0的解集为（）

A、（﹣2，1） B、（﹣∞，﹣2）∪（1，+∞） C、（﹣∞，﹣1）∪（2，+∞） D、（﹣1，2）

查看试题解析
8. 某观察站C与两灯塔A、B的距离分别为a米和b米，测得灯塔A在观察站C西偏北60°，灯塔B在观察站C北偏东60°，则两灯塔A、B间的距离为（）

A、 $\sqrt{a^{2} + b^{2}}$ 米 B、 $\sqrt{a^{2} + b^{2} - a b}$ 米 C、 $\sqrt{a^{2} + b^{2} + a b}$ 米 D、 $\sqrt{a^{2} + b^{2} - \sqrt{3} a b}$ 米

查看试题解析
9. 设m，n，l为空间不重合的直线，α，β，γ是空间不重合的平面，则下列说法准确的个数是（）
①m∥l，n∥l，则m∥n；②m⊥l，n⊥l，则m∥n；③若m∥l，m∥α，则l∥α； ④若l∥m，l⊂α，m⊂β，则α∥β；⑤若m⊂α，m∥β，l⊂β，l∥α，则α∥β⑥α∥γ，β∥γ，则α∥β．

A、0 B、1 C、2 D、3

查看试题解析
10. 设M是△ABC内一点，且S_△_ABC的面积为2，定义f（M）=（m，n，p），其中m，n，p分别是△MBC，△MCA，△MAB的面积，若△ABC内一动点P满足f（P）=（1，x，y），则 $\frac{1}{x} + \frac{4}{y}$ 的最小值是（）

A、1 B、4 C、9 D、12

查看试题解析
11. 若一个正三棱柱的主视图如图所示，其顶点都在一个球面上，则该球的表面积为（）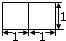

A、 $\frac{16 π}{3}$ B、 $\frac{19 π}{3}$ C、 $\frac{19 π}{12}$ D、 $\frac{4 π}{3}$

查看试题解析
12. 定义 $\frac{n}{p_{1} + p_{2} + \dots + p_{n}}$ 为n个正数p₁ ， p₂ ， …，p_n的“均倒数”．若已知正数数列{a_n}的前n项的“均倒数”为 $\frac{1}{2 n + 1}$ ，又b_n= $\frac{a_{n} + 1}{4}$ ，则 $\frac{1}{b_{1} b_{2}}$ + $\frac{1}{b_{2} b_{3}}$ + $\frac{1}{b_{3} b_{4}}$ +…+ $\frac{1}{b_{2015} b_{2016}}$ =（）

A、 $\frac{2013}{2014}$ B、 $\frac{2014}{2015}$ C、 $\frac{2015}{2016}$ D、 $\frac{1}{2015}$

查看试题解析

二、填空题

13. 若直线mx﹣（m+2）y+2=0与3x﹣my﹣1=0互相垂直，则点（m，1）到y轴的距离为．

查看试题解析
14. 已知圆锥的母线长为5cm，侧面积为15πcm² ，则此圆锥的体积为 cm³ ．

查看试题解析
15. 若实数x、y满足 ${\begin{matrix} y \geq 0 \\ x - 2 y \geq 2 \\ x + y \leq 5 \end{matrix}$ ，则x+2y的最小值是．

查看试题解析
16. 已知点p（x，y）是直线kx+y+4=0（k＞0）上一动点，PA、PB是圆C：x²+y²﹣2y=0的两条切线，A、B是切点，若四边形PACB的最小面积是2，则k的值为．

查看试题解析

三、解答题

17. 在△ABC中，角A，B，C所对的边分别为a，b，c，满足（2b﹣c）cosA=acosC．

(1)、求角A；

(2)、若 $a = \sqrt{13}$ ，b+c=5，求△ABC的面积．

查看试题解析
18. 如图，在四棱锥P﹣ABCD中，底面ABCD的平行四边形，∠ADC=60°， $A B = \frac{1}{2} A D$ ，PA⊥面ABCD，E为PD的中点．
（Ⅰ）求证：AB⊥PC
（Ⅱ）若PA=AB= $\frac{1}{2} A D = 2$ ，求三棱锥P﹣AEC的体积．

查看试题解析
19. 已知{a_n}是各项为正数的等比数列，{b_n}是等差数列，且a₁=b₁=1，b₂+b₃=2a₃ ， a₅﹣3b₂=7．

(1)、求{a_n}和{b_n}的通项公式；

(2)、设c_n=a_nb_n ， n∈N^* ，求数列{c_n}的前n项和为S_n ．

查看试题解析
20. 已知圆C：（x+2）²+y²=5，直线l：mx﹣y+1+2m=0，m∈R．

(1)、求证：对m∈R，直线l与圆C总有两个不同的交点A、B；

(2)、求弦AB的中点M的轨迹方程，并说明其轨迹是什么曲线；

(3)、是否存在实数m，使得圆C上有四点到直线l的距离为 $\frac{4 \sqrt{5}}{5}$ ？若存在，求出m的范围；若不存在，说明理由．

查看试题解析
21. 如图，三棱柱ABC﹣A₁B₁C₁的底面是边长为2的正三角形且侧棱垂直于底面，侧棱长是 $\sqrt{3}$ ，D是AC的中点．

(1)、求证：B₁C∥平面A₁BD；

(2)、求二面角A₁﹣BD﹣A的大小；

(3)、求直线AB₁与平面A₁BD所成的角的正弦值．

查看试题解析
22. 数列{a_n}的前n项和为S_n ，且S_n=n（n+1），n∈N^* ．

(1)、求数列{a_n}的通项公式；

(2)、若数列{b_n}满足： $a_{n} = \frac{b_{1}}{3 + 1} + \frac{b_{2}}{3^{2} + 1} + \dots + \frac{b_{n}}{3^{n} + 1}$ ，求数列{b_n}的通项公式；

(3)、令 $c_{n} = \frac{a_{n} b_{n}}{4} ， n \in N^{*}$ ，求数列{c_n}的前n项和T_n ．

查看试题解析