河北省衡水市深州中学2016-2017学年高一下学期数学期末考试试卷

试卷日期：2017-11-23 考试类型：期末考试

前去【出卷网】下载

一、选择题

1. 已知集合A={x|x＞0}，函数f（x）= $\sqrt{2 - x}$ 的定义域为集合B，则A∩B=（）

A、（0，+∞） B、（2，+∞） C、（﹣∞，2] D、（0，2]

查看试题解析
2. 已知 $c o s α = - \frac{4}{5}$ 且 $α \in (\frac{π}{2} ， π)$ ，则sin（ $α + \frac{π}{4})$ 等于（）

A、 $\frac{7 \sqrt{2}}{10}$ B、﹣ $\frac{\sqrt{2}}{10}$ C、 $\frac{\sqrt{2}}{10}$ D、﹣ $\frac{7 \sqrt{2}}{10}$

查看试题解析
3. 下列函数中，既是偶函数，又在（1，4）上单调递减的为（）

A、y=3x⁴﹣2x B、y=3^|^x^| C、y=e^x﹣e^﹣^x D、 $y = l o g_{\frac{1}{2}} | x |$

查看试题解析
4. 在△ABC中，AB=4，BC=3，∠ABC=60°，则AC=（）

A、13 B、 $\sqrt{13}$ C、37 D、 $\sqrt{37}$

查看试题解析
5. 某公司为对本公司的160名员工的身体状况进行调查，先将员工随机编号为1，2，3，…，159，160，采用系统抽样的方法（等间距地抽取，每段抽取一个个体）将抽取的一个样本．已知抽取的员工中最小的两个编号为5，21，那么抽取的员工中，最大的编号应该是（）

A、141 B、142 C、149 D、150

查看试题解析
6. 由直线y=x+1上的一点向圆（x﹣3）²+y²=1引切线，则切线长的最小值为（）

A、1 B、2 $\sqrt{2}$ C、 $\sqrt{7}$ D、3

查看试题解析
7. 某程序框图如图所示，则该程序运行后输出的值是（）

A、0 B、﹣1 C、﹣2 D、﹣8

查看试题解析
8. 已知cos（α﹣ $\frac{π}{6}$ ）+sinα= $\frac{4}{5} \sqrt{3}$ ，则sin（α+ $\frac{7 π}{6}$ ）的值是（）

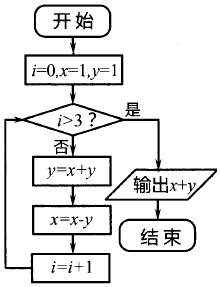A、 $\frac{4}{5}$ B、﹣ $\frac{4}{5}$ C、﹣ $\frac{3}{5}$ D、 $\frac{3}{5}$

查看试题解析
9. 如图所示，某几何体的三视图中，正视图和侧视图都是腰长为1的等腰直角三角形，则该几何体的体积为（）

A、 $\frac{1}{6}$ B、 $\frac{1}{3}$ C、1 D、 $1 + \sqrt{2}$

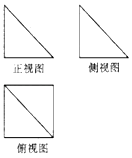查看试题解析
10. 已知函数f（x）=Asin（ωx+φ）（A，ω，φ为常数，A＞0，ω＞0，|φ|＜π）的部分图象如图所示，则下列结论正确的是（）

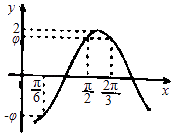A、函数f（x）的最小正周期为 $\frac{π}{2}$ B、直线x=﹣ $\frac{π}{12}$ 是函数f（x）图象的一条对称轴 C、函数f（x）在区间[﹣ $\frac{5 π}{12}$ ， $\frac{π}{6}$ ]上单调递增 D、将函数f（x）的图象向左平移 $\frac{π}{3}$ 个单位，得到函数g（x）的图象，则g（x）=2sin2x

查看试题解析
11. 已知函数f（x）=2sin（2x）﹣1，在[0， $\frac{π}{2}]$ 上随机取一个数a，则f（a）＞0的概率是（）

A、 $\frac{2}{3}$ B、 $\frac{1}{3}$ C、 $\frac{5}{6}$ D、 $\frac{1}{2}$

查看试题解析
12. 若a＜b＜c，则函数f（x）=（x﹣a）（x﹣b）+（x﹣b）（x﹣c）+（x﹣c）（x﹣a）的两个零点分别位于区间（）

A、（a，b）和（b，c）内 B、（﹣∞，a）和（a，b）内 C、（b，c）和（c，+∞）内 D、（﹣∞，a）和（c，+∞）内

查看试题解析

二、填空题

13. 设函数f（x）=3^x+9^x ，则f（log₃2）= ．

查看试题解析
14. 设向量 $\vec{e_{1}}$ ， $\vec{e_{2}}$ 是夹角为 $\frac{2 π}{3}$ 的单位向量，若 $\vec{a}$ = $\vec{e_{1}}$ + $\vec{e_{2}}$ ，则| $\vec{a}$ |= ．

查看试题解析
15. 一个均匀的正四面体的表面上分别标有数字1，2，3，4，现随机投掷两次，得到朝下的面上的数字分别为a，b，若方程x²﹣ax﹣b=0至少有一根m∈{1，2，3，4}，就称该方程为“漂亮方程”，则方程为“漂亮方程”的概率为．

查看试题解析
16. 已知三棱锥P﹣ABC中，PA=4，AB=AC=2 $\sqrt{3}$ ，BC=6，PA⊥平面ABC，则此三棱锥的外接球的半径为．

查看试题解析

三、解答题

17. 已知函数 $f (x) = s i n (2 x + \frac{π}{6}) + 2 c o s^{2} x$ ．

(1)、求函数y=f（x）的周期，并写出其单调递减区间；

(2)、当 $x \in [0 ， \frac{π}{2}]$ 时，求f（x）的最大值与最小值．

查看试题解析
18. 2015年下学期某市教育局对某校高三文科数学进行教学调研，从该校文科生中随机抽取40名学生的数学成绩进行统计，将他们的成绩分成六段[80，90），[90，100），[100，110），[110，120），[120，130），[130，140）后得到如图所示的频率分布直方图．

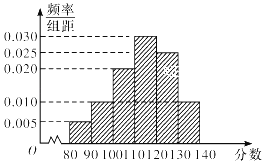(1)、求这40名学生中数学成绩不低于120分的学生人数；

(2)、若从数学成绩[80，100）内的学生中任意抽取2人，求成绩在[80，90）中至少有一人的概率．

查看试题解析
19. 在正三棱柱ABC﹣A₁B₁C₁中，点D是BC的中点．

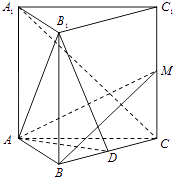(1)、求证：A₁C∥平面AB₁D；

(2)、设M为棱CC₁的点，且满足BM⊥B₁D，求证：平面AB₁D⊥平面ABM．

查看试题解析
20. 已知向量 $\vec{a}$ = $(c o s \frac{3}{2} x ， s i n \frac{3}{2} x)$ ， $\vec{b}$ = $(c o s \frac{x}{2} ， - s i n \frac{x}{2})$ ，且 $x \in [0 ， \frac{π}{2}]$

(1)、求 $\vec{a} \cdot \vec{b}$ 及| $\vec{a} + \vec{b}$ |

(2)、若f（x）= $\vec{a} \cdot \vec{b}$ ﹣2λ| $\vec{a} + \vec{b}$ |的最小值为 $- \frac{3}{2}$ ，求正实数λ的值．

查看试题解析
21. 在△ABC中，a，b，c分别是内角A，B，C的对边，且（a+c）²=b²+3ac
（Ⅰ）求角B的大小；
（Ⅱ）若b=2，且sinB+sin（C﹣A）=2sin2A，求△ABC的面积．

查看试题解析
22. 已知圆C：x²+y²+2x﹣4y+3=0．

(1)、若圆C的切线在x轴、y轴上的截距相等，求切线的方程；

(2)、从圆C外一点P（x₁ ， y₁）向圆引一条切线，切点为M，O为坐标原点，且有|PM|=|PO|，求使|PM|最小的点P的坐标．

查看试题解析