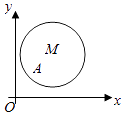河北省邯郸市2016-2017学年高一下学期数学期末考试试卷

试卷日期：2017-11-23 考试类型：期末考试

前去【出卷网】下载

一、选择题

1. 计算sin $\frac{7 π}{6}$ =（）

A、 $\frac{1}{2}$ B、 $- \frac{1}{2}$ C、 $\frac{\sqrt{3}}{2}$ D、 $- \frac{\sqrt{3}}{2}$

查看试题解析
2. 已知向量 $\vec{a}$ =（2，1）， $\vec{b}$ =（x，﹣2），若 $\vec{a}$ ∥ $\vec{b}$ ，则 $\vec{a}$ + $\vec{b}$ 等于（　　）

A、（﹣2，﹣1） B、（2，1） C、（3，﹣1） D、（﹣3，1）

查看试题解析
3. 如图是2007年在广州举行的全国少数民族运动会上，七位评委为某民族舞蹈打出的分数的茎叶统计图，去掉一个最高分和一个最低分后，所剩数据的平均数和方差分别为（）

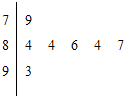A、84，4.84 B、84，1.6 C、85，1.6 D、85，4

查看试题解析
4. 已知圆C圆心是直线x﹣y+1=0与x轴的交点，且圆C与直线x+y+3=0相切，则圆C的方程是（）

A、（x+1）²+y²=2 B、（x﹣1）²+y²=2 C、（x+1）²+y²=8 D、（x﹣1）²+y²=8

查看试题解析
5. 若以连续掷两次骰子分别得到的点数m，n作为点P的坐标，求点P落在圆x²+y²=16外部的概率是（）

A、 $\frac{5}{9}$ B、 $\frac{2}{3}$ C、 $\frac{7}{9}$ D、 $\frac{8}{9}$

查看试题解析
6. 要得到函数y= $\sqrt{3}$ sin2x+cos2x的图象，只需将函数y=2sin2x的图象（）

A、向左平移 $\frac{π}{6}$ 个单位 B、向右平移 $\frac{π}{6}$ 个单位 C、向左平移 $\frac{π}{12}$ 个单位 D、向右平移 $\frac{π}{12}$ 个单位

查看试题解析
7. 如图是计算1 $+ \frac{1}{3} + \frac{1}{5} + \dots + \frac{1}{19}$ 的值的程序框图，则图中①、②处应填写的语句分别是（）

A、n=n+2，i＞10？ B、n=n+2，i≥10？ C、n=n+1，i＞10？ D、n=n+1，i≥10？

查看试题解析
8. 任取x∈[﹣ $\frac{π}{6}$ ， $\frac{π}{2}$ ]，则使 sinx+cosx∈[1， $\sqrt{2}$ ]的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{3}{4}$ C、 $\frac{2}{3}$ D、 $\frac{1}{3}$

查看试题解析
9. 平面上有四个互异的点A，B，C，D，已知（ $\vec{D B} + \vec{D C} - 2 \vec{D A}$ ） $\cdot \vec{C B}$ =0，则△ABC的形状为（）

A、直角三角形 B、等腰三角形 C、等腰直角三角形 D、等边三角形

查看试题解析
10. 已知ω＞0，函数f（x）=sin（ωx+ $\frac{π}{3}$ ）在（ $\frac{π}{2}$ ，π）上单调递减，则ω的取值范围是）

A、[ $\frac{1}{3}$ ， $\frac{7}{6}$ ] B、[ $\frac{1}{3}$ ， $\frac{5}{6}$ ] C、[0， $\frac{1}{3}$ ] D、[0，3]

查看试题解析
11. 已知直线2x+y﹣k=0（k＞0）与圆x²+y²=4交于不同的两点A，B，O是坐标原点，且有| $\vec{O A} + \vec{O B}$ | $\geq \frac{\sqrt{3}}{3}$ | $\vec{A B}$ |，那么k的取值范围是（）

A、[ $\sqrt{5}$ ，+∞） B、[ $\sqrt{5}$ ，2 $\sqrt{5}$ ） C、[ $\sqrt{3}$ ，+∞） D、[ $\sqrt{3}$ ，2 $\sqrt{5}$ ）

查看试题解析
12. 已知定义在R上的奇函数f（x），满足f（x﹣2）=﹣f（x），且当x∈[0，1]时，f（x）=x²+x+sinx，若方程f（x）=m（m＞0）在区间[﹣4，4]上有四个不同的根x₁ ， x₂ ， x₃ ， x₄ ，则x₁+x₂+x₃+x₄的值为（）

A、2 B、﹣2 C、4 D、﹣4

查看试题解析

二、填空题

13. 在一次对人体脂肪百分比和年龄关系的研究中，研究人员获得如下一组样本数据：
年龄x
21
24
34
41
脂肪y
9.5
17.5
24.9
28.1
由表中数据求得y关于x的线性回归方程为 $\hat{y}$ =0.6x $+ \hat{a}$ ，若年龄x的值为45，则脂肪含量y的估计值为．

查看试题解析
14. 已知tanα=﹣ $\frac{1}{2}$ ，则cos²α﹣sin²α的值为．

查看试题解析
15. 若圆C：x²+（y﹣2）²=5与恒过点P（0，1）的直线交于A，B两点，则弦AB的中点M的轨迹方程为．

查看试题解析
16. 如图，半径为1的扇形AOB的圆心角为120°，点C在 $\hat{A B}$ 上，且∠COA=30°，若 $\vec{O C}$ = $λ \vec{O A} + μ \vec{O B}$ ，则λ+μ ．

查看试题解析

三、解答题

17. 已知 $\vec{a}$ ， $\vec{b}$ 为两个非零向量，且| $\vec{a}$ |=2，| $\vec{b}$ |=1，（ $\vec{a}$ + $\vec{b}$ ） $⊥ \vec{b}$ ．
（Ⅰ）求 $\vec{a}$ 与 $\vec{b}$ 的夹角
（Ⅱ）求|3 $\vec{a} - 2 \vec{b}$ |．

查看试题解析
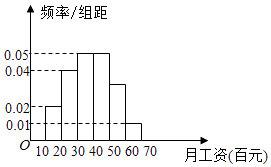
18. 某地政府调查了工薪阶层1000人的月工资收入，并根据调查结果画出如图所示的频率分布直方图，其中工资收入分组区间是[10，15），[15，20），[20，25），[25，30）[30，35），[35，40]（单位：百元）
（Ⅰ）为了了解工薪阶层对工资收入的满意程度，要用分层抽样的方法从调查的1000人中抽取100人做电话询问，求月工资收入在[30，35）内应抽取的人数；
（Ⅱ）根据频率分布直方图估计这1000人的平均月工资为多少元．

查看试题解析
19. 已知cos（π+α）= $\frac{4}{5}$ ，且 $\frac{π}{2}$ ＜α＜π．
（Ⅰ）求5sin（α+π）﹣4tan（3π﹣α）的值
（Ⅱ）若0＜β＜ $\frac{π}{2}$ ，cos（β﹣α）= $\frac{\sqrt{5}}{5}$ ，求sin（ $\frac{π}{2}$ +2β）的值．

查看试题解析
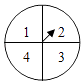
20. 游乐场推出了一项趣味活动，参加活动者需转动如图所示的转盘两次，每次转动后，待转盘停止转动时，记录指针所指区域中的数，设两次记录的数分别为x，y，奖励规则如下：
①若xy≤3，则奖励玩具一个；②若xy≥8，则奖励水杯一个；③其余情况奖励饮料一瓶，假设转盘质地均匀，四个区域划分均匀，小亮准备参加此项活动．
（Ⅰ）求小亮获得玩具的概率；
（Ⅱ）请比较小亮获得水杯与获得饮料的概率的大小，并说明理由．

查看试题解析
21. 已知 $\vec{a}$ =（2cosωx，cosωx）， $\vec{b}$ =（cosωx，2 $\sqrt{3}$ sinωx），函数f（x）= $\vec{a} \cdot \vec{b}$ +m（其中ω＞0，m∈R），且f（x）的图象在y轴右侧的第一个最高点的横坐标为 $\frac{π}{6}$ ，并过点（0，2）．
（Ⅰ）求函数f（x）的解析式及其单调增区间；
（Ⅱ）若对任意x₁ ， x₂∈[0， $\frac{π}{2}$ ]，都有|f（x₁）﹣f（x₂）|≤a，求实数a的取值范围．

查看试题解析
22. 如图，在平面直角坐标系xOy中，已知以M为圆心的圆M：x²+y²﹣12x﹣14y+60=0及其上的一点A（2，4）．
（Ⅰ）是否存在直线l：y=kx+3与圆M有两个交点B，C，并且|AB|=|AC|，若有，求此直线方程，若没有，请说明理由；
（Ⅱ）设点T（t，0）满足：存在圆M上的两点P和Q，使得 $\vec{T A} + \vec{T P}$ = $\vec{T Q}$ ，求实数t的取值范围．

查看试题解析

年龄x	21	24	34	41
脂肪y	9.5	17.5	24.9	28.1