河北省保定市2016-2017学年高一下学期数学期末考试试卷

试卷日期：2017-11-23 考试类型：期末考试

前去【出卷网】下载

一、选择题

1. 已知等差数列{a_n}中，a₁=1，d=2，则a₁₀=（）

A、19 B、22 C、23 D、24

查看试题解析
2. 在正方体ABCD﹣A₁B₁C₁D₁中，直线A₁C₁与平面DBB₁D₁所成的角为（）

A、30° B、45° C、60° D、90°

查看试题解析
3. 若等比数列{a_n}的前n项和S_n=3ⁿ﹣1，则其公比为（）

A、﹣3 B、3 C、﹣1 D、1

查看试题解析
4. 已知直线l，m，平面α，β且l⊥α，m⊂β，给出下列四个命题中，正确命题的个数为（）
⑴若α∥β，则l⊥m
⑵若l⊥m，则α∥β
⑶若α⊥β，则l⊥m
⑷若l∥m，则α⊥β

A、1 B、2 C、3 D、4

查看试题解析
5. 在等差数列{a_n}中，若a₁、a₁₀是方程2x²+5x+1=0的两个根，则公差d（d＞0）为（）

A、 $\frac{\sqrt{17}}{18}$ B、 $\frac{\sqrt{15}}{11}$ C、 $\frac{\sqrt{3}}{2}$ D、 $\frac{1}{2}$

查看试题解析
6. 不等式组 ${\begin{matrix} x^{2} - 1 < 0 \\ x^{2} - 3 x \geq 0 \end{matrix}$ 的解集是（）

A、{x|﹣1＜x＜1} B、{x|1＜x≤3} C、{x|﹣1＜x≤0} D、{x|x≥3或x＜1}

查看试题解析
7. 若直线x+y=0与圆x²+（y﹣a）²=1相切，则a的值为（）

A、1 B、±1 C、 $\sqrt{2}$ D、± $\sqrt{2}$

查看试题解析
8. 若变量x，y满足 ${\begin{matrix} x - 4 y + 3 \leq 0 ， \\ 3 x + 5 y < 25 ， \\ x \geq 1 ， \end{matrix}$ 则目标函数z=2x+y的最小值为（）

A、1 B、2 C、3 D、4

查看试题解析
9. 已知等比数列{a_n}满足a₁=3，且3a₁ ， 2a₂ ， a₃成等差数列，则公比等于（）

A、1或3 B、1或9 C、3 D、9

查看试题解析
10. 如图，两个正方形ABCD和ADEF所在平面互相垂直，设M、N分别是BD和AE的中点，那么①AD⊥MN；②MN∥平面CDE；③MN∥CE；④MN、CE异面．其中假命题的个数为（）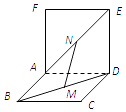

A、4 B、3 C、2 D、1

查看试题解析
11. 设三棱柱的侧棱垂直于底面，所有棱的长都为3，顶点都在同一个球面上，则该球的表面积为（）

A、2π B、 $\frac{4}{3}$ π C、21π D、23π

查看试题解析
12. 定义：在数列{a_n}中，若a_n²﹣a_n_﹣₁²=p，（n≥2，n∈N^* ， p为常数），则称{a_n}为“等方差数列”，下列是对“等方差数列”的有关判断：
①若{a_n}是“等方差数列”，则数列{ $\frac{1}{a_{n}}$ }是等差数列；
②{（﹣2）ⁿ}是“等方差数列”；
③若{a_n}是“等方差数列”，则数列{a_kn}（k∈N^* ， k为常数）也是“等方差数列”；
④若{a_n}既是“等方差数列”，又是等差数列，则该数列是常数数列．
其中正确命题的个数为（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

13. 已知直线l₁：x+my﹣2=0，l₂：mx+y+1=0，若l₁⊥l₂ ，则m= ．

查看试题解析
14. 在圆x²+y²﹣2x﹣6y=0内，过点E（0，1）的最长弦和最短弦之积为．

查看试题解析
15. 一个几何体的三视如图所示，其中正视图和俯视图均为腰长为2的等腰直角三角形，则用个这样的几何体可以拼成一个棱长为2的正方体．

查看试题解析
16. 已知数列{a_n}满足a₁=3，a_n_﹣₁a_na_n₊₁=3（n≥2），T_n=a₁a₂…a_n ，则log₃T₂₀₁₇= ．

查看试题解析

三、解答题

17. 若不等式ax²﹣bx+c＞0的解集为{x|﹣2＜x＜3}，求不等式cx²﹣bx﹣a＜0的解集．

查看试题解析
18. 已知△ABC中，内角A，B，C依次成等差数列，其对边分别为a，b，c，且b= $\sqrt{2}$ asinB．

(1)、求内角C；

(2)、若b=2，求△ABC的面积．

查看试题解析
19. 已知直线l经过点M（﹣3，﹣3），且圆x²+y²+4y﹣21=0的圆心到l的距离为 $\sqrt{5}$ ．

(1)、求直线l被该圆所截得的弦长；

(2)、求直线l的方程．

查看试题解析
20. 设数列{a_n}的前n项和为S_n ，且S_n+a_n=1，数列{b_n}为等差数列，且b₁+b₂=b₃=3．

(1)、求S_n；

(2)、求数列（a_nb_n）的前n项和T_n ．

查看试题解析
21. 为了培养学生的数学建模和应用能力，某校组织了一次实地测量活动，如图，假设待测量的树木AE的高度H（m），垂直放置的标杆BC的高度h=4m，仰角∠ABE=α，∠ADE=β（D，C，E三点共线），试根据上述测量方案，回答如下问题：

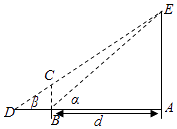(1)、若测得α=60°、β=30°，试求H的值；

(2)、经过分析若干次测得的数据后，大家一致认为适当调整标杆到树木的距离d（单位：m），使α与β之差较大时，可以提高测量精确度．
若树木的实际高度为8m，试问d为多少时，α﹣β最大？

查看试题解析
22. 如图，正方体ABCD﹣A₁B₁C₁D₁中，M，N分别为AB，BC的中点．

(1)、求证：平面B₁MN⊥平面BB₁D₁D；

(2)、当点P在DD₁上运动时，是否都有MN∥平面A₁C₁P，证明你的结论；

(3)、若P是D₁D的中点，试判断PB与平面B₁MN是否垂直？请说明理由．

查看试题解析