河北省石家庄三十二中2017年中考数学模拟试卷
试卷日期:2017-11-21 考试类型:中考模拟
一、选择题
-
1. 若等式﹣2□(﹣2)=4成立,则“□”内的运算符号是( )A、+ B、﹣ C、× D、÷2. 已知28a2bm÷4anb2=7b2 , 那么m、n的值为( )A、m=4,n=2 B、m=4,n=1 C、m=1,n=2 D、m=2,n=23. 下列四个图案中,属于中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 某厂接到加工720件衣服的订单,预计每天做48件,正好按时完成,后因客户要求提前5天交货,设每天应多做x件才能按时交货,则x应满足的方程为( )A、 B、 = C、 D、5. 当k>0时,正比例函数y=kx的图象大致是( )A、
4. 某厂接到加工720件衣服的订单,预计每天做48件,正好按时完成,后因客户要求提前5天交货,设每天应多做x件才能按时交货,则x应满足的方程为( )A、 B、 = C、 D、5. 当k>0时,正比例函数y=kx的图象大致是( )A、 B、
B、 C、
C、 D、
D、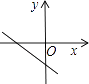 6. 如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长为( )
6. 如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长为( ) A、1.8 B、2.4 C、3.2 D、3.67. 若代数式 有意义,则x的取值范围是( )A、x>1且x≠2 B、x≥1 C、x≠2 D、x≥1且x≠28. 如图所示的几何体的俯视图是( )
A、1.8 B、2.4 C、3.2 D、3.67. 若代数式 有意义,则x的取值范围是( )A、x>1且x≠2 B、x≥1 C、x≠2 D、x≥1且x≠28. 如图所示的几何体的俯视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 9. 三角形是( )A、连接任意三点组成的图形 B、由不在同一条直线上的三条线段首尾顺次相接所成的图形 C、由三条线段组成的图形 D、以上说法均不对10. 如图,在CD上求一点P,使它到OA,OB的距离相等,则P点是( )
9. 三角形是( )A、连接任意三点组成的图形 B、由不在同一条直线上的三条线段首尾顺次相接所成的图形 C、由三条线段组成的图形 D、以上说法均不对10. 如图,在CD上求一点P,使它到OA,OB的距离相等,则P点是( ) A、线段CD的中点 B、OA与OB的中垂线的交点 C、OA与CD的中垂线的交点 D、CD与∠AOB的平分线的交点11. 如图,数轴上点M所表示的数可能是( )
A、线段CD的中点 B、OA与OB的中垂线的交点 C、OA与CD的中垂线的交点 D、CD与∠AOB的平分线的交点11. 如图,数轴上点M所表示的数可能是( )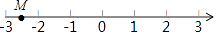 A、1.5 B、﹣1.6 C、﹣2.6 D、﹣3.412. 甲乙两地相距420千米,新修的高速公路开通后,在甲、乙两地行驶的长途客运车平均速度是原来的1.5倍,进而从甲地到乙地的时间缩短了2小时.设原来的平均速度为x千米/时,可列方程为( )A、 + =2 B、 ﹣ =2 C、 + = D、 ﹣ =13. 如图:在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于M,若CM=5,则CE2+CF2等于( )
A、1.5 B、﹣1.6 C、﹣2.6 D、﹣3.412. 甲乙两地相距420千米,新修的高速公路开通后,在甲、乙两地行驶的长途客运车平均速度是原来的1.5倍,进而从甲地到乙地的时间缩短了2小时.设原来的平均速度为x千米/时,可列方程为( )A、 + =2 B、 ﹣ =2 C、 + = D、 ﹣ =13. 如图:在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于M,若CM=5,则CE2+CF2等于( ) A、75 B、100 C、120 D、12514. 方程2x(x﹣3)=5(x﹣3)的解是( )A、x=3 B、x= C、x1=3,x2= D、x=﹣315. 如图,DE∥BC,在下列比例式中,不能成立的是( )
A、75 B、100 C、120 D、12514. 方程2x(x﹣3)=5(x﹣3)的解是( )A、x=3 B、x= C、x1=3,x2= D、x=﹣315. 如图,DE∥BC,在下列比例式中,不能成立的是( )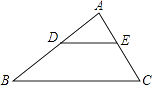 A、 = B、 = C、 = D、 =16. 若二次函数y=ax2+bx+c(a≠0)的图象上有两点,坐标分别为(x1 , y1),(x2 , y2),其中x1<x2 , y1y2<0,则下列判断正确的是( )A、a<0 B、a>0 C、方程ax2+bx+c=0必有一根x0满足x1<x0<x2 D、y1<y2
A、 = B、 = C、 = D、 =16. 若二次函数y=ax2+bx+c(a≠0)的图象上有两点,坐标分别为(x1 , y1),(x2 , y2),其中x1<x2 , y1y2<0,则下列判断正确的是( )A、a<0 B、a>0 C、方程ax2+bx+c=0必有一根x0满足x1<x0<x2 D、y1<y2二、填空题:
-
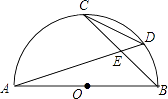
17. ﹣ 的绝对值的倒数是 .18. 把多项式2x2y﹣4xy2+2y3分解因式的结果是19. 如图,AB是⊙O直径,弦AD、BC相交于点E,若CD=5,AB=13,则 = .
三、计算题:
-
20. 计算:(﹣3)4÷(1.5)2﹣6×(﹣ )+|﹣32﹣9|.21. ﹣22÷(﹣1)2﹣ ×[4﹣(﹣5)2].
四、解答题:
-
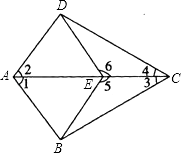
22. 已知:如图,在四边形ABCD中,E是AC上一点,∠1=∠2,∠3=∠4.求证:∠5=∠6.
 23. 如图,△ABC中BD、CD平分∠ABC、∠ACB,过D作直线平行于BC,交AB,AC于E,F,求证:EF=BE+CF.
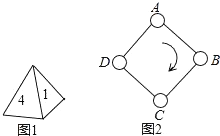
23. 如图,△ABC中BD、CD平分∠ABC、∠ACB,过D作直线平行于BC,交AB,AC于E,F,求证:EF=BE+CF.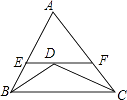 24. 如图1,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字1,2,3,4.如图2,正方形ABCD顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.
24. 如图1,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字1,2,3,4.如图2,正方形ABCD顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.如:若从圈A起跳,第一次掷得3,就顺时针连续跳3个边长,落到圈D;若第二次掷得2,就从D开始顺时针连续跳2个边长,落到圈B;…
设游戏者从圈A起跳.
 (1)、嘉嘉随机掷一次骰子,求落回到圈A的概率P1;(2)、淇淇随机掷两次骰子,用列表法求最后落回到圈A的概率P2 , 并指出她与嘉嘉落回到圈A的可能性一样吗?25. 为发展电信事业,方便用户,电信公司对移动电话采取不同的收费方式,其中,所使用的“便民卡”与“如意卡”在某市范围内每月(30天)的通话时间x(min)与通话费y(元)的关系如图所示:
(1)、嘉嘉随机掷一次骰子,求落回到圈A的概率P1;(2)、淇淇随机掷两次骰子,用列表法求最后落回到圈A的概率P2 , 并指出她与嘉嘉落回到圈A的可能性一样吗?25. 为发展电信事业,方便用户,电信公司对移动电话采取不同的收费方式,其中,所使用的“便民卡”与“如意卡”在某市范围内每月(30天)的通话时间x(min)与通话费y(元)的关系如图所示: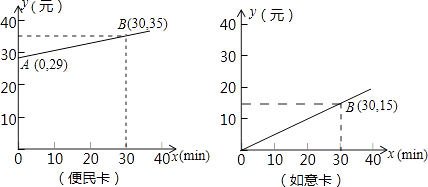 (1)、分别求出通话费y1 , y2与通话时间x之间的函数关系式;(2)、请帮用户计算,在一个月内使用哪一种卡便宜.26. 如图,一种某小区的两幢10层住宅楼间的距离为AC=30m,由地面向上依次为第1层、第2层、…、第10层,每层高度为3m.假设某一时刻甲楼在乙楼侧面的影长EC=h,太阳光线与水平线的夹角为α
(1)、分别求出通话费y1 , y2与通话时间x之间的函数关系式;(2)、请帮用户计算,在一个月内使用哪一种卡便宜.26. 如图,一种某小区的两幢10层住宅楼间的距离为AC=30m,由地面向上依次为第1层、第2层、…、第10层,每层高度为3m.假设某一时刻甲楼在乙楼侧面的影长EC=h,太阳光线与水平线的夹角为α (1)、用含α的式子表示h(不必指出α的取值范围);
(1)、用含α的式子表示h(不必指出α的取值范围);
(2)、用含α的式子表示h(不必指出α的取值范围);
27. 如图1,在Rt△ABC中,∠C=90°,BC=8厘米,点D在AC上,CD=3厘米.点P、Q分别由A、C两点同时出发,点P沿AC方向向点C匀速移动,速度为每秒k厘米,行完AC全程用时8秒;点Q沿CB方向向点B匀速移动,速度为每秒1厘米.设运动的时间为x秒(0<x<8),△DCQ的面积为y1平方厘米,△PCQ的面积为y2平方厘米. (1)、求y1与x的函数关系,并在图2中画出y1的图象;(2)、如图2,y2的图象是抛物线的一部分,其顶点坐标是(4,12),求点P的速度及AC的长;(3)、在图2中,点G是x轴正半轴上一点0<OG<6,过G作EF垂直于x轴,分别交y1、y2的图象于点E、F.
(1)、求y1与x的函数关系,并在图2中画出y1的图象;(2)、如图2,y2的图象是抛物线的一部分,其顶点坐标是(4,12),求点P的速度及AC的长;(3)、在图2中,点G是x轴正半轴上一点0<OG<6,过G作EF垂直于x轴,分别交y1、y2的图象于点E、F.①说出线段EF的长在图1中所表示的实际意义;
②当0<x<6时,求线段EF长的最大值.