河北省石家庄四十九中2017年中考数学模拟试卷

试卷日期：2017-11-07 考试类型：中考模拟

前去【出卷网】下载

一、选择题

1. 下列各对数互为相反数的是（）

A、4和﹣（﹣4） B、﹣3和 $\frac{1}{3}$ C、﹣2和﹣ $\frac{1}{2}$ D、0和0

查看试题解析
2. 若（x﹣3）（x+4）=x²+px+q，那么p、q的值是（　　）

A、p=1，q=﹣12 B、p=﹣1，q=12 C、p=7，q=12 D、p=7，q=﹣12

查看试题解析
3. 正三角形、正方形、等腰直角三角形、平行四边形中，既是轴对称图形又是中心对称图形的是（）

A、正三角形 B、正方形 C、等腰直角三角形 D、平行四边形

查看试题解析
4. 下列各式中，正确的是（）

A、 $\frac{a + b}{a b}$ = $\frac{1 + b}{b}$ B、 $\frac{x - y}{x + y}$ = $\frac{x^{2} - y^{2}}{{(x + y)}^{2}}$ C、 $\frac{x - 3}{x^{2} - 9}$ = $\frac{1}{x - 3}$ D、 $\frac{- x + y}{2}$ =﹣ $\frac{x + y}{2}$

查看试题解析
5. 下列说法正确的是（）

A、正比例函数是一次函数 B、一次函数是正比例函数 C、正比例函数不是一次函数 D、不是正比例函数就不是一次函数

查看试题解析
6. 若顺次连接四边形ABCD各边的中点所得四边形是菱形，则四边形ABCD一定是（）

A、菱形 B、对角线互相垂直的四边形 C、矩形 D、对角线相等的四边形

查看试题解析
7. 函数y= $\sqrt{x - 2}$ ，自变量x的取值范围是（）

A、x＞2 B、x＜2 C、x≥2 D、x≤2

查看试题解析
8. 如图是一个正方体的表面展开图，把展开图折叠成正方体后，与标号为1的顶点重合的是（）

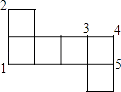A、标号为2的顶点 B、标号为3的顶点 C、标号为4的顶点 D、标号为5的顶点

查看试题解析
9. 已知AB=1.5，AC=4.5，若BC的长为整数，则BC的长为（）

A、3 B、6 C、3或6 D、4或5

查看试题解析
10. 如图，OP是∠AOB的平分线，点P到OA的距离为3，点N是OB上的任意一点，则线段PN的取值范围为（）

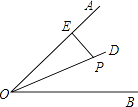A、PN＜3 B、PN＞3 C、PN≥3 D、PN≤3

查看试题解析
11. 如图，数轴上点M所表示的数可能是（）

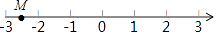A、1.5 B、﹣1.6 C、﹣2.6 D、﹣3.4

查看试题解析
12. 今年我市工业试验区投资50760万元开发了多个项目，今后还将投资106960万元开发多个新项目，每个新项目平均投资比今年每个项目平均投资多500万元，并且新增项目数量比今年多20个．假设今年每个项目平均投资是x万元，那么下列方程符合题意的是（）

A、 $\frac{106960}{x + 500}$ ﹣ $\frac{50760}{x}$ =20 B、 $\frac{50760}{x}$ ﹣ $\frac{106960}{x + 500}$ =20 C、 $\frac{106960}{x + 20}$ ﹣ $\frac{50760}{x}$ =500 D、 $\frac{50760}{x}$ ﹣ $\frac{106960}{x + 20}$ =500

查看试题解析
13. 如图，点E在正方形ABCD内，满足∠AEB=90°，AE=6，BE=8，则阴影部分的面积是（）

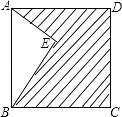A、48 B、60 C、76 D、80

查看试题解析
14. 方程2x（x﹣3）=5（x﹣3）的解是（）

A、x=3 B、x= $\frac{5}{2}$ C、x₁=3，x₂= $\frac{5}{2}$ D、x=﹣3

查看试题解析
15. 如图，在大小为4×4的正方形网格中，是相似三角形的是（）

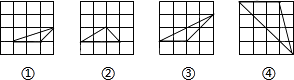A、①和② B、②和③ C、①和③ D、②和④

查看试题解析
16. 如图，在平面直角坐标系中，点A，B的坐标分别为（1，0），（0，2），某抛物线的顶点坐标为D（﹣1，1）且经过点B，连接AB，直线AB与此抛物线的另一个交点为C，则S_△_BCD：S_△_ABO=（）

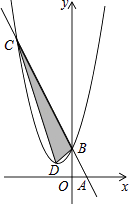A、8：1 B、6：1 C、5：1 D、4：1

查看试题解析

二、填空题：

17. 如果一个数的平方根是a+6和2a﹣15，则这个数为．

查看试题解析
18. 分解因式：ab²﹣2a²b+a³= ．

查看试题解析
19. 如图，锐角三角形ABC的边AB和AC上的高线CE和BF相交于点D．请写出图中的一对相似三角形，如．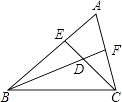

查看试题解析

三、计算题：

20. 计算：（﹣2）³÷ $\frac{4}{5}$ +3×|1﹣（﹣2）²|．

查看试题解析
21. 计算：﹣16÷（﹣2）³﹣|﹣ $\frac{1}{16}$ |×（﹣8）+[1﹣（﹣3）²]．

查看试题解析

四、解答题：

22. 如图，点A，C，D，B四点共线，且AC=BD，∠A=∠B，∠ADE=∠BCF，求证：DE=CF．

查看试题解析
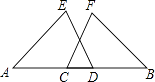23. 如图，△ABC中BD、CD平分∠ABC、∠ACB，过D作直线平行于BC，交AB，AC于E，F，求证：EF=BE+CF．

查看试题解析
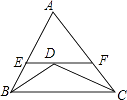24. 小美周末来到公园，发现在公园一角有一种“守株待兔”游戏．游戏设计者提供了一只兔子和一个有A，B，C，D，E五个出入口的兔笼，而且笼内的兔子从每个出入口走出兔笼的机会是均等的．规定：①玩家只能将小兔从A、B两个出入口放入，②如果小兔进入笼子后选择从开始进入的出入口离开，则可获得一只价值5元小兔玩具，否则每玩一次应付费3元．

(1)、请用表格或树状图求小美玩一次“守株待兔”游戏能得到小兔玩具的概率；

(2)、假设有1000人次玩此游戏，估计游戏设计者可赚多少元？

查看试题解析
25. 一水果经销商购进了A，B两种水果各10箱，分配给他的甲、乙两个零售店（分别简称甲店、乙店）销售，预计每箱水果的盈利情况如下表：

A种水果/箱
B种水果/箱
甲店
11元
17元
乙店
9元
13元

(1)、如果甲、乙两店各配货10箱，其中A种水果两店各5箱，B种水果两店各5箱，请你计算出经销商能盈利多少元？

(2)、在甲、乙两店各配货10箱（按整箱配送），且保证乙店盈利不小于100元的条件下，请你设计出使水果经销商盈利最大的配货方案，并求出最大盈利为多少？

查看试题解析
26. 如图，旗杆AB的顶端B在夕阳的余辉下落在一个斜坡上的点D处，某校数学课外兴趣小组的同学正在测量旗杆的高度，在旗杆的底部A处测得点D的仰角为15°，AC=10米，又测得∠BDA=45°．已知斜坡CD的坡度为i=1： $\sqrt{3}$ ，求旗杆AB的高度（ $\sqrt{3} \approx 1.7$ ，结果精确到个位）．

查看试题解析
27. 如图，二次函数 $y = - \frac{1}{4} x^{2} + b x + c$ 的图象经过点A（4，0），B（﹣4，﹣4），且与y轴交于点C．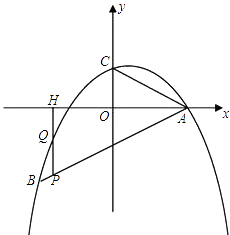

(1)、试求此二次函数的解析式；

(2)、试证明：∠BAO=∠CAO（其中O是原点）；

(3)、若P是线段AB上的一个动点（不与A、B重合），过P作y轴的平行线，分别交此二次函数图象及x轴于Q、H两点，试问：是否存在这样的点P，使PH=2QH？若存在，请求出点P的坐标；若不存在，请说明理由．

查看试题解析

	A种水果/箱	B种水果/箱
甲店	11元	17元
乙店	9元	13元