河北省石家庄九十七中2017年中考数学模拟试卷

试卷日期：2017-11-07 考试类型：中考模拟

前去【出卷网】下载

一、选择题

1. 陕西省元月份某一天的天气预报中，延安市的最低气温为﹣6℃，西安市的最低气温为2℃，这一天延安市的最低气温比西安市的最低气温低（）

A、8℃ B、﹣8℃ C、6℃ D、2℃

查看试题解析
2. 在①﹣a⁵•（﹣a）²；②（﹣a⁶）÷（﹣a³）；③（﹣a²）³•（a³）²；④[﹣（﹣a）²]⁵中计算结果为﹣a¹⁰的有（）

A、①② B、③④ C、②④ D、④

查看试题解析
3. 下列各图中，不是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 下列各式中，计算正确的是（）

A、3^﹣¹=﹣3 B、3^﹣³=﹣9 C、3^﹣²= $\frac{1}{9}$ D、3⁰=0

查看试题解析
5. 下列函数中，是一次函数的有（）
①y=πx ②y=2x﹣1 ③y= $\frac{1}{x}$ ④y=2﹣3x ⑤y=x²﹣1．

A、4个 B、3个 C、2个 D、1个

查看试题解析
6. 如图，平行四边形ABCD中，DB=DC，∠C=70°，AE⊥BD于E，则∠DAE等于（）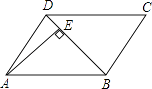

A、20° B、25° C、30° D、35°

查看试题解析
7. 在Rt△ABC中，∠C=90°，c为斜边，a、b为直角边，则化简 $\sqrt{{(a - b + c)}^{2}} - 2 | c - a - b |$ 的结果为（）

A、3a+b﹣c B、﹣a﹣3b+3c C、a+3b﹣3c D、2a

查看试题解析
8. 如图是一个水平放置的圆柱形物体，中间有一细棒，则此几何体的俯视图是（）

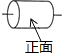A、 B、 C、 D、

查看试题解析
9. 用正四边形和正八边形镶嵌成一个平面，则在某一个顶点处，正四边形和正八边形的个数分别为（）

A、2个和1个 B、1个和2个 C、3个和1个 D、1个和3个

查看试题解析
10. 如图，△ABC的三边AB、BC、AC的长分别12，18，24，O是△ABC三条角平分线的交点，则S_△_OAB：S_△_OBC：S_△_OAC=（）

A、1：1：1 B、1：2：3 C、2：3：4 D、3：4：5

查看试题解析
11. 若a，b为有理数，a＞0，b＜0，且|a|＜|b|，那么a，b，﹣a，﹣b的大小关系是（）

A、b＜﹣a＜﹣b＜a B、b＜﹣b＜﹣a＜a C、b＜﹣a＜a＜﹣b D、﹣a＜﹣b＜b＜a

查看试题解析
12. 遂宁市某生态示范园，计划种植一批核桃，原计划总产量达36万千克，为了满足市场需求，现决定改良核桃品种，改良后平均每亩产量是原计划的1.5倍，总产量比原计划增加了9万千克，种植亩数减少了20亩，则原计划和改良后平均每亩产量各多少万千克？设原计划每亩平均产量x万千克，则改良后平均每亩产量为1.5x万千克，根据题意列方程为（）

A、 $\frac{36}{x}$ ﹣ $\frac{36 + 9}{1.5 x}$ =20 B、 $\frac{36}{x}$ ﹣ $\frac{36}{1.5 x}$ =20 C、 $\frac{36 + 9}{1.5 x}$ ﹣ $\frac{36}{x}$ =20 D、 $\frac{36}{x}$ + $\frac{36 + 9}{1.5 x}$ =20

查看试题解析
13. 在下列四组数中，不是勾股数的一组数是（　　）

A、a=15，b=8，c=17 B、a=9，b=12，c=15 C、a=7，b=24，c=25 D、a=3，b=5，c=7

查看试题解析
14. 关于x的方程kx²+3x﹣1=0有实数根，则k的取值范围是（）

A、k≤ $\frac{9}{4}$ B、k≥﹣ $\frac{9}{4}$ 且k≠0 C、k≥﹣ $\frac{9}{4}$ D、k＞﹣ $\frac{9}{4}$ 且k≠0

查看试题解析
15. 下列各组数中，成比例的是（）

A、﹣7，﹣5，14，5 B、﹣6，﹣8，3，4 C、3，5，9，12 D、2，3，6，12

查看试题解析
16. 二次函数y=ax²+bx+c（a，b，c为常数，且a≠0）中的x与y的部分对应值如下表：
X
﹣1
0
1
3
y
﹣1
3
5
3
下列结论：
①ac＜0；
②当x＞1时，y的值随x值的增大而减小．
③3是方程ax²+（b﹣1）x+c=0的一个根；
④当﹣1＜x＜3时，ax²+（b﹣1）x+c＞0．
其中正确的个数为（）

A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题：

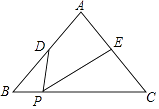
17. 计算： $\sqrt{9}$ ﹣2^﹣¹+ $\sqrt[3]{8}$ ﹣|﹣2|= ．

查看试题解析
18. 分解因式：xy﹣x﹣y+1= ．

查看试题解析
19. △ABC中，AB=AC=4，BC=5，点D是边AB的中点，点E是边AC的中点，点P是边BC上的动点，∠DPE=∠C，则BP= ．

查看试题解析

三、计算题：

20. 计算：﹣3³+（﹣1）²⁰¹⁶÷ $\frac{1}{6}$ +（﹣5）² ．

查看试题解析
21. ﹣0.5²+ $\frac{1}{4}$ ﹣|﹣3²﹣9|﹣（﹣1 $\frac{1}{2}$ ）³× $\frac{16}{27}$ ．

查看试题解析

四、解答题：

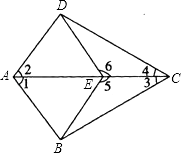
22. 已知：如图，在四边形ABCD中，E是AC上一点，∠1=∠2，∠3=∠4．求证：∠5=∠6．

查看试题解析
23. 如图，在△ABC中，AC=DC=DB，∠ACD=100°，求∠B的度数．

查看试题解析
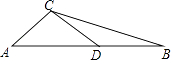24. 一袋中装有形状大小都相同的四个小球，每个小球上各标有一个数字，分别是1，4，7，8．现规定从袋中任取一个小球，对应的数字作为一个两位数的个位数；然后将小球放回袋中并搅拌均匀，再任取一个小球，对应的数字作为这个两位数的十位数．

(1)、写出按上述规定得到所有可能的两位数；

(2)、从这些两位数中任取一个，求其算术平方根大于4且小于7的概率．

查看试题解析
25. 建立一次函数关系解决问题：甲、乙两校为了绿化校园，甲校计划购买A种树苗，A种树苗每棵24元；乙校计划购买B种树苗，B种树苗每棵18元．两校共购买了35棵树苗．若购进B种树苗的数量少于A种树苗的数量，请给出一种两校总费用最少的方案，并求出该方案所需的总费用．

查看试题解析
26.
如图，某电信部门计划修建一条连接B、C两地的电缆．测量人员在山脚A点测得B、C两地的仰角分别为30°、45°，在B地测得C地的仰角为60°．已知C地比A地高200m，电缆BC至少长多少米（精确到1m）？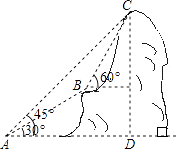

查看试题解析
27. 如图，在平面直角坐标系中，抛物线y=ax²+bx+c（a≠0）与x轴相交于A，B两点，与y轴相交于点C，直线y=kx+n（k≠0）经过B，C两点，已知A（1，0），C（0，3），且BC=5．

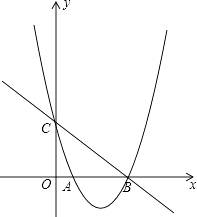(1)、分别求直线BC和抛物线的解析式（关系式）；

(2)、在抛物线的对称轴上是否存在点P，使得以B，C，P三点为顶点的三角形是直角三角形？若存在，请求出点P的坐标；若不存在，请说明理由．

查看试题解析

X	﹣1	0	1	3
y	﹣1	3	5	3