湖南省邵阳市邵阳县黄亭中学2016-2017学年中考数学二模试卷
试卷日期:2017-10-26 考试类型:中考模拟
一、选择题
-
1. ﹣ 的倒数是( )A、 B、﹣2 C、2 D、﹣2. 如图,已知点A(﹣8,0),B(2,0),点C在直线y=﹣ 上,则使△ABC是直角三角形的点C的个数为( )
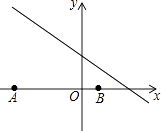 A、1 B、2 C、3 D、43. 在一个不透明的盒子中装有12个白球,若干个黄球,它们除颜色不同外,其余均相同.若从中随机摸出一个球是白球的概率是 ,则黄球的个数为( )
A、1 B、2 C、3 D、43. 在一个不透明的盒子中装有12个白球,若干个黄球,它们除颜色不同外,其余均相同.若从中随机摸出一个球是白球的概率是 ,则黄球的个数为( )
A、18 B、20 C、24 D、284. 如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )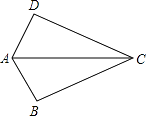 A、CB=CD B、∠BAC=∠DAC C、∠BCA=∠DCA D、∠B=∠D=90°5. 已知两圆半径分别为3、5,圆心距为8,则这两圆的位置关系为( )
A、CB=CD B、∠BAC=∠DAC C、∠BCA=∠DCA D、∠B=∠D=90°5. 已知两圆半径分别为3、5,圆心距为8,则这两圆的位置关系为( )
A、外离 B、内含 C、相交 D、外切6. 如图所示,是由5个相同的小正方体组合而成的几何体,它的左视图是( )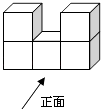 A、
A、 B、
B、 C、
C、 D、
D、 7. 下列图形中,既是中心对称,又是轴对称图形的是( )A、
7. 下列图形中,既是中心对称,又是轴对称图形的是( )A、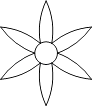 B、
B、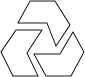 C、
C、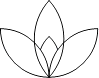 D、
D、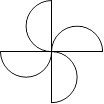 8. 已知如图,一次函数y=ax+b和反比例函数y= 的图象相交于A、B两点,不等式ax+b> 的解集为( )
8. 已知如图,一次函数y=ax+b和反比例函数y= 的图象相交于A、B两点,不等式ax+b> 的解集为( )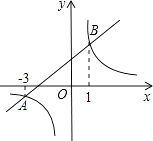 A、x<﹣3 B、﹣3<x<0或x>1 C、x<﹣3或x>1 D、﹣3<x<19. 甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500米,先到终点的人原地休息.已知甲先出发2秒.在跑步过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,给出以下结论:①a=8;②b=92;③c=123.其中正确的是( )
A、x<﹣3 B、﹣3<x<0或x>1 C、x<﹣3或x>1 D、﹣3<x<19. 甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500米,先到终点的人原地休息.已知甲先出发2秒.在跑步过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,给出以下结论:①a=8;②b=92;③c=123.其中正确的是( )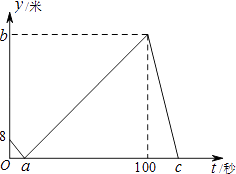 A、①②③ B、仅有①② C、仅有①③ D、仅有②③
A、①②③ B、仅有①② C、仅有①③ D、仅有②③二、填空题
-
10. 20140000用科学记数法表示(保留3个有效数字)为 .
11. 已知甲组数据的平均数为 甲 , 乙组数据的平均数为 乙 , 且 甲= 乙 , 而甲组数据的方差为S2甲=1.25,乙组数据的方差为S2乙=3,则较稳定.
12. 点P(﹣2,3)关于x轴对称的点的坐标为 . 关于y轴对称的点的坐标为 .13. 如图,直线AB∥CD,CA平分∠BCD,若∠1=50°,则∠2= .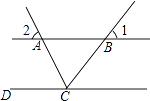 14. 如图,AB是⊙O的直径,AB=15,AC=9,则tan∠ADC= .
14. 如图,AB是⊙O的直径,AB=15,AC=9,则tan∠ADC= .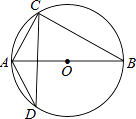 15. 如图,将矩形纸片ABCD折叠,使边AB,CB均落在对角线BD上,得折痕BE,BF,则∠EBF=°.
15. 如图,将矩形纸片ABCD折叠,使边AB,CB均落在对角线BD上,得折痕BE,BF,则∠EBF=°.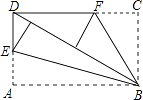 16. 在平面直角坐标系中,对于平面内任一点(m,n),规定以下两种变换:
16. 在平面直角坐标系中,对于平面内任一点(m,n),规定以下两种变换:①f(m,n)=(m,﹣n),如f(2,1)=(2,﹣1);
②g(m,n)=(﹣m,﹣n),如g (2,1)=(﹣2,﹣1)
按照以上变换有:f[g(3,4)]=f(﹣3,﹣4)=(﹣3,4),那么g[f(﹣3,2)]= .
三、解答题
-
17. 计算:( )﹣2+(π﹣2014)0+sin60°+| ﹣2|.18. 解方程: .
19. 如图,△ABC、△CDE均为等腰直角三角形,∠ACB=∠DCE=90°,点E在AB上.求证:△CDA≌△CEB.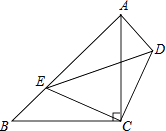
四、解答题
-
20. 某酒厂每天生产A,B两种品牌的白酒共600瓶,A,B两种品牌的白酒每瓶的成本和利润如下表:
设每天生产A种品牌白酒x瓶,每天获利y元.
(1)、请写出y关于x的函数关系式;
(2)、如果该酒厂每天至少投入成本26400元,那么每天至少获利多少元?A
B
成本(元/瓶)
50
35
利润(元/瓶)
20
15
21. 某调查小组采用简单随机抽样方法,对某市部分中小学生一天中阳光体育运动时间进行了抽样调查,并把所得数据整理后绘制成如下的统计图: (1)、该调查小组抽取的样本容量是多少?(2)、求样本学生中阳光体育运动时间为1.5小时的人数,并补全占频数分布直方图;
(1)、该调查小组抽取的样本容量是多少?(2)、求样本学生中阳光体育运动时间为1.5小时的人数,并补全占频数分布直方图;
(3)、请估计该市中小学生一天中阳光体育运动的平均时间.22. 如图,为了测量山顶铁塔AE的高,小明在27m高的楼CD底部D测得塔顶A的仰角为45°,在楼顶C测得塔顶A的仰角36°52′.已知山高BE为56m,楼的底部D与山脚在同一水平线上,求该铁塔的高AE.(参考数据:sin36°52′≈0.60,tan36°52′≈0.75)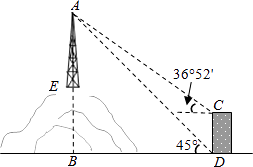
五、综合题
-
23. 如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,交AB于点E,过点D作DF⊥AB,垂足为F,连接DE.
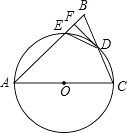 (1)、求证:直线DF与⊙O相切;(2)、若AE=7,BC=6,求AC的长.
(1)、求证:直线DF与⊙O相切;(2)、若AE=7,BC=6,求AC的长.
24. 如图所示,在平面直角坐标系中,抛物线y=ax2+bx+c经过A(﹣3,0)、B(1,0)、C(0,3)三点,其顶点为D,连接AD,点P是线段AD上一个动点(不与A、D重合),过点P作y轴的垂线,垂足点为E,连接AE.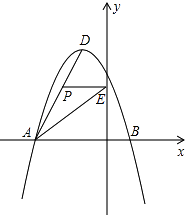 (1)、求抛物线的函数解析式,并写出顶点D的坐标;(2)、如果P点的坐标为(x,y),△PAE的面积为S,求S与x之间的函数关系式,直接写出自变量x的取值范围,并求出S的最大值;(3)、在(2)的条件下,当S取到最大值时,过点P作x轴的垂线,垂足为F,连接EF,把△PEF沿直线EF折叠,点P的对应点为点P′,求出P′的坐标,并判断P′是否在该抛物线上.
(1)、求抛物线的函数解析式,并写出顶点D的坐标;(2)、如果P点的坐标为(x,y),△PAE的面积为S,求S与x之间的函数关系式,直接写出自变量x的取值范围,并求出S的最大值;(3)、在(2)的条件下,当S取到最大值时,过点P作x轴的垂线,垂足为F,连接EF,把△PEF沿直线EF折叠,点P的对应点为点P′,求出P′的坐标,并判断P′是否在该抛物线上.