河北省石家庄四十中2016-2017学年中考数学模拟试卷
试卷日期:2017-10-26 考试类型:中考模拟
一、选择题
-
1. 如果规定收入为正,支出为负.收入500 元记作500元,那么支出237元应记作( )
A、﹣500元 B、﹣237元 C、237元 D、500元2. 若a+b=5,ab=﹣24,则a2+b2的值等于( )A、73 B、49 C、43 D、233. 下列各图中,不是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 4. 两个小组同时从甲地出发,匀速步行到乙地,甲乙两地相距7500米,第一组的步行速度是第二组的1.2倍,并且比第二组早15分钟到达乙地.设第二组的步行速度为x千米/小时,根据题意可列方程是( )A、 ﹣ =15 B、 ﹣ = C、 ﹣ =15 D、 ﹣ =5. 函数y=3x+1的图象一定经过点( )
4. 两个小组同时从甲地出发,匀速步行到乙地,甲乙两地相距7500米,第一组的步行速度是第二组的1.2倍,并且比第二组早15分钟到达乙地.设第二组的步行速度为x千米/小时,根据题意可列方程是( )A、 ﹣ =15 B、 ﹣ = C、 ﹣ =15 D、 ﹣ =5. 函数y=3x+1的图象一定经过点( )
A、(3,5) B、(﹣2,3) C、(2,7) D、(4,10)6. 如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,若BF=12,AB=10,则AE的长为( ) A、13 B、14 C、15 D、167. 在函数y= 中,自变量x的取值范围是( )A、x≤1 B、x≥1 C、x<1 D、x>18. 下面的四个图形都是由大小相同的正方形组成的,其中能围成正方体的是( )A、
A、13 B、14 C、15 D、167. 在函数y= 中,自变量x的取值范围是( )A、x≤1 B、x≥1 C、x<1 D、x>18. 下面的四个图形都是由大小相同的正方形组成的,其中能围成正方体的是( )A、 B、
B、 C、
C、 D、
D、 9. 若一个正多边形的一个外角是45°,则这个正多边形的边数是( )A、10 B、9 C、8 D、610. 如图,△ABC的三边AB,BC,CA长分别是20,30,40,其三条角平分线将△ABC分为三个三角形,则S△ABO:S△BCO:S△CAO等于( )
9. 若一个正多边形的一个外角是45°,则这个正多边形的边数是( )A、10 B、9 C、8 D、610. 如图,△ABC的三边AB,BC,CA长分别是20,30,40,其三条角平分线将△ABC分为三个三角形,则S△ABO:S△BCO:S△CAO等于( )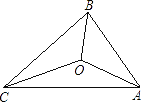 A、1:1:1 B、1:2:3 C、2:3:4 D、3:4:511. 如图所示的图形为四位同学画的数轴,其中正确的是( )A、
A、1:1:1 B、1:2:3 C、2:3:4 D、3:4:511. 如图所示的图形为四位同学画的数轴,其中正确的是( )A、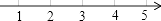 B、
B、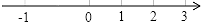 C、
C、 D、
D、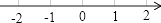 12. 某工厂现在平均每天比原计划多生产50台机器,现在生产600台机器所需时间与原计划生产450台机器所需时间相同.设原计划平均每天生产x台机器,根据题意,下面所列方程正确的是( )A、 = B、 = C、 = D、 =13. 点A(﹣3,﹣4)到原点的距离为( )A、3 B、4 C、5 D、714. 方程x2+6x﹣5=0的左边配成完全平方后所得方程为( )A、(x+3)2=14 B、(x﹣3)2=14 C、(x+3)2=4 D、(x﹣3)2=415. 如图,在矩形ABCD中,E、F分别是CD、BC上的点.若∠AEF=90°,则一定有( )
12. 某工厂现在平均每天比原计划多生产50台机器,现在生产600台机器所需时间与原计划生产450台机器所需时间相同.设原计划平均每天生产x台机器,根据题意,下面所列方程正确的是( )A、 = B、 = C、 = D、 =13. 点A(﹣3,﹣4)到原点的距离为( )A、3 B、4 C、5 D、714. 方程x2+6x﹣5=0的左边配成完全平方后所得方程为( )A、(x+3)2=14 B、(x﹣3)2=14 C、(x+3)2=4 D、(x﹣3)2=415. 如图,在矩形ABCD中,E、F分别是CD、BC上的点.若∠AEF=90°,则一定有( )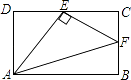 A、△ADE∽△ECF B、△BCF∽△AEF C、△ADE∽△AEF D、△AEF∽△ABF16. 已知二次函数y=ax2+bx+c(a≠0)的图象如图,其对称轴为直线x=﹣1,给出下列结果:(1)b2>4ac;(2)abc>0;(3)2a+b=0;(4)a+b+c>0;(5)a﹣b+c<0.
A、△ADE∽△ECF B、△BCF∽△AEF C、△ADE∽△AEF D、△AEF∽△ABF16. 已知二次函数y=ax2+bx+c(a≠0)的图象如图,其对称轴为直线x=﹣1,给出下列结果:(1)b2>4ac;(2)abc>0;(3)2a+b=0;(4)a+b+c>0;(5)a﹣b+c<0.则正确的结论是( )
 A、(1)(2)(3)(4) B、(2)(4)(5) C、(2)(3)(4) D、(1)(4)(5)
A、(1)(2)(3)(4) B、(2)(4)(5) C、(2)(3)(4) D、(1)(4)(5)二、填空题:
-
17. 点A在数轴上和原点相距3个单位长度,点B在数轴上和原点相距 个单位长度,则A、B两点这间的距离是 .18. 如图,一次函数y=kx+3分别与x,y轴交于点N,M,与反比例函数y= (x>0)的图象交于点A,若AM:MN=2:3,则k= .
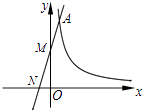
三、计算题:
-
19. 计算:﹣12016﹣[2﹣(﹣1)2016]÷(﹣ )× .20. 计算:(﹣2)3×8×( )3+8÷ .
四、解答题:
-
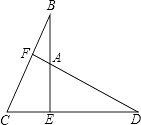
21. 已知:BE⊥CD,BE=DE,BC=DA,
求证:①△BEC≌△DEA;
②DF⊥BC.
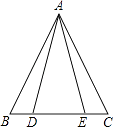
 22. 如图,已知D、E两点在线段BC上,AB=AC,AD=AE.
22. 如图,已知D、E两点在线段BC上,AB=AC,AD=AE.证明:BD=CE.
 23. 在四张编号为A,B,C,D的卡片(除编号外,其余完全相同)的正面分别写上如图所示的正整数后,背面向上,洗匀放好.
23. 在四张编号为A,B,C,D的卡片(除编号外,其余完全相同)的正面分别写上如图所示的正整数后,背面向上,洗匀放好. (1)、我们知道,满足a2+b2=c2的三个正整数a,b,c成为勾股数,嘉嘉从中随机抽取一张,求抽到的卡片上的数是勾股数的概率P1;(2)、琪琪从中随机抽取一张(不放回),再从剩下的卡片中随机抽取一张(卡片用A,B,C,D表示).请用列表或画树形图的方法求抽到的两张卡片上的数都是勾股数的概率P2 , 并指出她与嘉嘉抽到勾股数的可能性一样吗?24. 某市在城中村改造中,需要种植A、B两种不同的树苗共3000棵,经招标,承包商以15万元的报价中标承包了这项工程,根据调查及相关资料表明,A、B两种树苗的成本价及成活率如表:
(1)、我们知道,满足a2+b2=c2的三个正整数a,b,c成为勾股数,嘉嘉从中随机抽取一张,求抽到的卡片上的数是勾股数的概率P1;(2)、琪琪从中随机抽取一张(不放回),再从剩下的卡片中随机抽取一张(卡片用A,B,C,D表示).请用列表或画树形图的方法求抽到的两张卡片上的数都是勾股数的概率P2 , 并指出她与嘉嘉抽到勾股数的可能性一样吗?24. 某市在城中村改造中,需要种植A、B两种不同的树苗共3000棵,经招标,承包商以15万元的报价中标承包了这项工程,根据调查及相关资料表明,A、B两种树苗的成本价及成活率如表:品种
购买价(元/棵)
成活率
A
28
90%
B
40
95%
设种植A种树苗x棵,承包商获得的利润为y元.
(1)、求y与x之间的函数关系式;(2)、政府要求栽植这批树苗的成活率不低于93%,承包商应如何选种树苗才能获得最大利润?最大利润是多少?25. 已知:如图,斜坡AP的坡度为1:2.4,坡长AP为26米,在坡顶A处的同一水平面上有一座古塔BC,在斜坡底P处测得该塔的塔顶B的仰角为45°,在坡顶A处测得该塔的塔顶B的仰角为76°.求: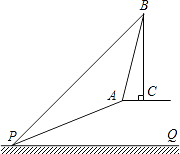 (1)、坡顶A到地面PQ的距离;(2)、古塔BC的高度(结果精确到1米).(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)26. 已知抛物线y=ax2﹣4a(a>0)与x轴相交于A,B两点(点A在点B的左侧),点P是抛物线上一点,且PB=AB,∠PBA=120°,如图所示.
(1)、坡顶A到地面PQ的距离;(2)、古塔BC的高度(结果精确到1米).(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)26. 已知抛物线y=ax2﹣4a(a>0)与x轴相交于A,B两点(点A在点B的左侧),点P是抛物线上一点,且PB=AB,∠PBA=120°,如图所示.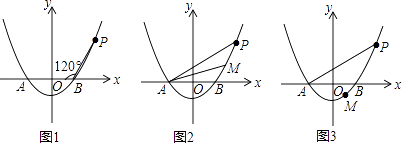 (1)、求抛物线的解析式.(2)、设点M(m,n)为抛物线上的一个动点,且在曲线PA上移动.
(1)、求抛物线的解析式.(2)、设点M(m,n)为抛物线上的一个动点,且在曲线PA上移动.①当点M在曲线PB之间(含端点)移动时,是否存在点M使△APM的面积为 ?若存在,求点M的坐标;若不存在,请说明理由.
②当点M在曲线BA之间(含端点)移动时,求|m|+|n|的最大值及取得最大值时点M的坐标.