上海市金山中学2016-2017学年高一上学期数学期中考试试卷

试卷日期：2017-10-19 考试类型：期中考试

前去【出卷网】下载

一、填空题

1. 若全集U={1，2，3，4，5}，且∁_UA={2，3}，则集合A= ．

查看试题解析
2. 已知集合A={﹣1，0，1}， $B = {x | \frac{x + 1}{x - 1} < 0}$ ，则A∩B= ．

查看试题解析
3. 函数f（x）= $\frac{x - 3}{x + 3}$ ，g（x）=x+3，则f（x）•g（x）= ．

查看试题解析
4. 函数f（x）= $\frac{\sqrt{x - 1}}{x - 2}$ 的定义域为．

查看试题解析
5. 设函数f（x）= ${\begin{matrix} - x ， x \leq 0 \\ x^{2} ， x > 0 \end{matrix}$ ，若f（a）=2，则实数a= ．

查看试题解析
6. 若0＜a＜1，则不等式（a﹣x）（x﹣ $\frac{1}{a}$ ）＞0的解集为．

查看试题解析
7. 已知p：x²+x﹣2＞0，q：x＞a，若q是p的充分不必要条件，则q的取值范围是．

查看试题解析
8. 若关于x的不等式|ax﹣2|＜3的解集为{x|﹣ $\frac{5}{3}$ ＜x＜ $\frac{1}{3}$ }，则a= ．

查看试题解析
9. 若关于x的不等式（a﹣1）x²+2（a﹣1）x﹣4≥0的解集为∅，则实数a的取值范围是

查看试题解析
10. 已知集合A={﹣1，2}，B={x|mx+1＞0}，若A∪B=B，则实数m的取值范围是．

查看试题解析
11. 设函数f（x）=x﹣2，若不等式|f（x+3）|＞|f（x）|+m对任意实数x恒成立，则m的取值范围是．

查看试题解析
12. 满足不等式|x﹣A|＜B（B＞0，A∈R）的实数x的集合叫做A的B邻域，若a+b﹣2的a+b邻域是一个关于原点对称的区间，则 $\frac{1}{a} + \frac{4}{b}$ 的取值范围是．

查看试题解析

二、选择题

13. 若集合中三个元素为边可构成一个三角形，则该三角形一定不可能是（）

A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰三角形

查看试题解析
14. 设x取实数，则f（x）与g（x）表示同一个函数的是（）

A、f（x）=x，g（x）= $\sqrt{x^{2}}$ B、f（x）= $\frac{{(\sqrt{x})}^{2}}{x}$ ，g（x）= $\frac{x}{{(\sqrt{x})}^{2}}$ C、f（x）=1，g（x）=（x﹣1）⁰ D、f（x）= $\frac{x^{2} - 9}{x + 3}$ ，g（x）=x﹣3

查看试题解析
15. 若a和b均为非零实数，则下列不等式中恒成立的是（）

A、 $\frac{a^{2} + b^{2}}{2} \geq {(\frac{a + b}{2})}^{2}$ B、 $\frac{b}{a} + \frac{a}{b} \geq 2$ C、 $(a + b) (\frac{1}{a} + \frac{1}{b}) \geq 4$ D、 $\frac{| a + b |}{2} \geq \sqrt{| a b |}$

查看试题解析
16. 若一系列函数的解析式相同，值域相同，但定义域不同，则称这些函数为“孪生函数”，那么函数解析式为y=2x²+1，值域为{5，19}的“孪生函数”共有（　　）

A、4个 B、6个 C、8个 D、9个

查看试题解析

三、解答下列各题

17. 解不等式组 ${\begin{matrix} \frac{x - 2}{x - 1} < 1 \\ - x^{2} + x + 2 < 0 \end{matrix}$ ．

查看试题解析
18. 已知集合A={x|x²﹣px﹣2=0}，B={x|x²+qx+r=0}，若A∪B={﹣2，1，5}，A∩B={﹣2}，求p+q+r的值．

查看试题解析
19. 已知集合P={a|不等式x²+ax+ $\frac{1}{16}$ ≤0有解}，集合Q={a|不等式ax²+4ax﹣4＜0对任意实数x恒成立}，求P∩Q．

查看试题解析
20. 我校为进行“阳光运动一小时”活动，计划在一块直角三角形ABC的空地上修建一个占地面积为S（平方米）的矩形AMPN健身场地．如图，点M在AC上，点N在AB上，且P点在斜边BC上．已知∠ACB=60°，|AC|=30米，|AM|=x米，x∈[10，20]．设矩形AMPN健身场地每平方米的造价为 $\frac{37 k}{\sqrt{S}}$ 元，再把矩形AMPN以外（阴影部分）铺上草坪，每平方米的造价为 $\frac{12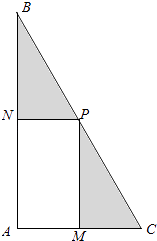 k}{\sqrt{S}}$ 元（k为正常数）．

(1)、试用x表示S，并求S的取值范围；

(2)、求总造价T关于面积S的函数T=f（S）；

(3)、如何选取|AM|，使总造价T最低（不要求求出最低造价）．

查看试题解析
21. 设函数 $g (x) = \sqrt{x} + 1$ ，函数 $h (x) = \frac{1}{x + 3} ， x \in (- 3 ， a]$ ，其中a为常数且a＞0，令函数f（x）=g（x）•h（x）．

(1)、求函数f（x）的表达式，并求其定义域；

(2)、当 $a = \frac{1}{4}$ 时，求函数f（x）的值域；

(3)、是否存在自然数a，使得函数f（x）的值域恰为 $[\frac{1}{3} ， \frac{1}{2}]$ ？若存在，试写出所有满足条件的自然数a所构成的集合；若不存在，试说明理由．

查看试题解析