江苏省盐城市东台市第一教研片2017-2018学年九年级上学期数学第一次阶段检测试卷
试卷日期:2017-10-18 考试类型:月考试卷
一、精心选一选
-
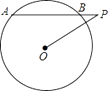
1. 下列方程中,是一元二次方程的为( )A、 B、 C、 D、2. 已知OA=4cm,以O为圆心,r为半径作⊙O.若使点A在⊙O内,则r的值可以是( )A、2cm B、3cm C、4cm D、5cm3. 方程x 2﹣5x=0的解是( )A、x1=0,x2=﹣5 B、x=5 C、x1=0,x2=5 D、x=04. 下列说法中,不正确的是( )A、过圆心的弦是圆的直径 B、等弧的长度一定相等 C、周长相等的两个圆是等圆 D、同一条弦所对的两条弧一定是等弧5. 如图,⊙O的半径是3,点P是弦AB延长线上的一点,连接OP,若OP=4,∠APO=30°,则弦AB的长为( )
 A、 B、 C、 D、6. 一元二次方程 的根的情况是( )
A、 B、 C、 D、6. 一元二次方程 的根的情况是( )
A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法判断7. 如图,△ABC内接于⊙O,BD是直径.若 ,则 等于( )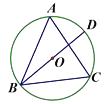 A、 B、 C、 D、8. 如图,半圆O的直径AB=10cm,弦AC=6cm,AD平分∠BAC,则AD长( )
A、 B、 C、 D、8. 如图,半圆O的直径AB=10cm,弦AC=6cm,AD平分∠BAC,则AD长( )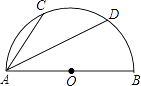 A、4 cm B、3 cm C、5 cm D、4 cm
A、4 cm B、3 cm C、5 cm D、4 cm二、用心做一做
-
9. 方程 的解为。10. 已知x=2是方程 的一个根,则m的值是 .
11. 如图,⊙O直径AB=8,∠CBD=30°,则CD= .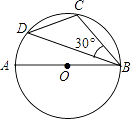 12. 已知点P为平面内一点,若点P 到⊙O上的点的最长距离为5,最短距离为1,则⊙O 的半径为 .
12. 已知点P为平面内一点,若点P 到⊙O上的点的最长距离为5,最短距离为1,则⊙O 的半径为 .
13. 菱形ABCD的一条对角线长为6,边AB的长是方程 的一个根,则菱形ABCD的周长为 .
14. 如图,⊙O的内接四边形ABCD中,∠A=110°,则∠BOD等于°. 15. 已知圆锥的侧面积为 cm2 , 侧面展开图的圆心角为45°,则该圆锥的母线长为 cm。
15. 已知圆锥的侧面积为 cm2 , 侧面展开图的圆心角为45°,则该圆锥的母线长为 cm。
16. 若实数a、b满足 ,则 .
17. 若一个三角形的三边长均满足方程x2﹣6x+8=0,则此三角形的周长为 .
18. 如图,MN是⊙O的直径,MN=2,点A在⊙O上,∠AMN=30°,B为弧AN的中点,P是直径MN上一动点,则PA+PB的最小值为 .
三、专心解一解
-
19. 解下列方程:
(1)、(2x-1)2=4
(2)、 (用配方法)
(3)、x2+2x=4.
(4)、
20. 已知:关于x的方程x2+2mx+m2﹣1=0(1)、不解方程,判别方程根的情况;(2)、若方程有一个根为3,求m的值.21. 在等腰△ABC中,三边分别为a、b、c,其中 ,若关于x的方程 有两个相等的实数根,求△ABC的周长.22. 某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,下图是水平放置的破裂管道有水部分的截面. (1)、请你补全这个输水管道的圆形截面;(2)、若这个输水管道有水部分的水面宽AB=16cm,水面最深地方的高度为4cm,求这个圆形截面的半径.23. 如图,AB是⊙O的弦,点C、D在AB上,且AC=BD.判断△OCD的形状,并说明理由.
(1)、请你补全这个输水管道的圆形截面;(2)、若这个输水管道有水部分的水面宽AB=16cm,水面最深地方的高度为4cm,求这个圆形截面的半径.23. 如图,AB是⊙O的弦,点C、D在AB上,且AC=BD.判断△OCD的形状,并说明理由.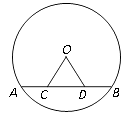 24. 如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D, AC交⊙O于点E,∠BAC=45°。
24. 如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D, AC交⊙O于点E,∠BAC=45°。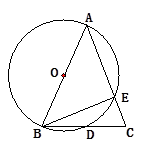 (1)、求∠EBC的度数;(2)、求证:BD=CD。25. 如图,点B、C、D都在⊙O上,过C点作CA∥BD交OD的延长线于点A,连接BC,∠B=∠A=30°,BD=4 .
(1)、求∠EBC的度数;(2)、求证:BD=CD。25. 如图,点B、C、D都在⊙O上,过C点作CA∥BD交OD的延长线于点A,连接BC,∠B=∠A=30°,BD=4 .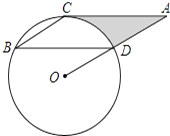 (1)、求证:AC是⊙O的切线;(2)、求由线段AC、AD与弧CD所围成的阴影部分的面积.(结果保留π)26. 如图有一圆锥形粮堆,其主视图是边长为6m的正三形ABC。
(1)、求证:AC是⊙O的切线;(2)、求由线段AC、AD与弧CD所围成的阴影部分的面积.(结果保留π)26. 如图有一圆锥形粮堆,其主视图是边长为6m的正三形ABC。 (1)、求该圆锥形粮堆的侧面积。(2)、母线AC的中点P处有一老鼠正在偷吃粮食,小猫从B处沿圆锥表面去偷袭老鼠,求小猫经过的最短路程。(结果不取近似数)27. 如图,A(-5,0),B(-3,0),点C在y轴的正半轴上,∠CBO=45°,CD∥AB.∠CDA=90°.点P从点Q(4,0)出发,沿x轴向左以每秒1个单位长度的速度运动,运动时时间t秒.
(1)、求该圆锥形粮堆的侧面积。(2)、母线AC的中点P处有一老鼠正在偷吃粮食,小猫从B处沿圆锥表面去偷袭老鼠,求小猫经过的最短路程。(结果不取近似数)27. 如图,A(-5,0),B(-3,0),点C在y轴的正半轴上,∠CBO=45°,CD∥AB.∠CDA=90°.点P从点Q(4,0)出发,沿x轴向左以每秒1个单位长度的速度运动,运动时时间t秒.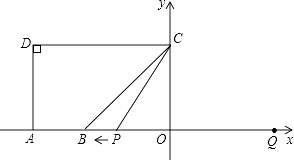 (1)、求点C的坐标;(2)、当∠BCP=15°时,求t的值;(3)、以点P为圆心,PC为半径的⊙P随点P的运动而变化,当⊙P与四边形ABCD的边(或边所在的直线)相切时,求t的值.
(1)、求点C的坐标;(2)、当∠BCP=15°时,求t的值;(3)、以点P为圆心,PC为半径的⊙P随点P的运动而变化,当⊙P与四边形ABCD的边(或边所在的直线)相切时,求t的值.