北京市昌平区2017年高考理数二模试卷

试卷日期：2017-10-16 考试类型：高考模拟

前去【出卷网】下载

一、选择题

1. 设集合A={x|﹣1≤x＜2}，B={x|x²＜1}，则A∩B=（　　）

A、{x|1＜x＜2} B、{x|﹣1＜x＜1} C、{x|﹣1≤x＜2} D、{x|﹣1≤x＜1}

查看试题解析
2. 下列函数中，在其定义域上既是奇函数又是增函数的是（　　）

A、y=2^x B、y=sinx C、y=x³ D、y=ln|x|

查看试题解析
3. 执行如图所示的程序框图，若输出的S值为 $\frac{1}{3}$ ，则①处应填写（　　）

A、k＜3 B、k＜4 C、k＜5 D、k＜6

查看试题解析
4. 在△ABC中，已知AB=3，AC=5，A=120°，则 $\frac{s i n A}{s i n B}$ =（　　）

A、 $\frac{5}{7}$ B、 $\frac{7}{5}$ C、 $\frac{3}{5}$ D、 $\frac{5}{3}$

查看试题解析
5. 命题p：数列{a_n}的前n项和S_n=an²+bn+c（a≠0）；命题q：数列{a_n}是等差数列．则p是q的（　　）

A、充分而不必要条件 B、必要而不充分条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
6. 第五届北京农业嘉年华于2017年3月11日至5月7日在昌平区兴寿镇草莓博览园中举办，设置“三馆两园一带一谷一线”八大功能板块．现安排六名志愿者去其中的“三馆两园”参加志愿者服务工作，若每个“馆”与“园”都至少安排一人，则不同的安排方法种数为（　　）

A、C $_{6}^{2}$ A $_{5}^{5}$ B、5C $_{6}^{1}$ A $_{5}^{5}$ C、5A $_{5}^{5}$ D、C $_{6}^{1}$ A $_{5}^{5}$

查看试题解析
7. 设点A（0，1），B（2，﹣1），点C在双曲线M： $\frac{x^{2}}{4}$ ﹣y²=1上，则使△ABC的面积为3的点C的个数为（　　）

A、4 B、3 C、2 D、1

查看试题解析
8. 四支足球队进行单循环比赛（每两队比赛一场），每场比赛胜者得3分，负者得0分，平局双方各得1分．比赛结束后发现没有足球队全胜，且四队得分各不相同，则所有比赛中最多可能出现的平局场数是（　　）

A、2 B、3 C、4 D、5

查看试题解析

二、填空题

9. 设 a∈R，若（1+i）（a﹣i）=﹣2i，则a= ．

查看试题解析
10. 若实数x，y满足 ${\begin{matrix} x - y + 1 \geq 0 \\ x + y \geq 0 \\ x \leq 0 \end{matrix}$ ，则2x+y的最小值为．

查看试题解析
11. 已知 $\vec{a}$ =（1， $\sqrt{3}$ ）， $\vec{b}$ =（﹣1，0）， $\vec{c}$ =（ $\sqrt{3}$ ，k），若2 $\vec{a}$ ﹣ $\vec{b}$ 与 $\vec{c}$ 垂直，则k= ．

查看试题解析
12. 在极坐标中，点（ $\sqrt{2}$ ， $\frac{π}{4}$ ）到直线ρcosθ=2的距离等于．

查看试题解析
13. 在空间直角坐标系O﹣xyz中，已知A（2，0，0），B（0，2，0），C（0，0，0），P（0，1， $\sqrt{3}$ ），则三棱锥P﹣ABC在坐标平面xOz上的正投影图形的面积为；该三棱锥的最长棱的棱长为．

查看试题解析
14. 若函数f（x）= . （a＞0且a≠1），函数g（x）=f（x）﹣k．
①若a= $\frac{1}{3}$ ，函数g（x）无零点，则实数k的取值范围为；
②若f（x）有最小值，则实数a的取值范围是．

查看试题解析

三、解答题

15. 已知函数f（x）=2sinxsin（ $\frac{π}{6}$ ﹣x）．
（Ⅰ）求f（ $\frac{π}{3}$ ）及f（x）的最小正周期T的值；
（Ⅱ）求f（x）在区间[﹣ $\frac{π}{6}$ ， $\frac{π}{4}$ ]上的最大值和最小值．

查看试题解析
16. 从某校随机抽取部分男生进行身体素质测试，获得掷实心球的成绩数据，整理得到数据分组及频率分布表，成绩在11.0米（精确到0.1米）以上（含）的男生为“优秀生”．
分组（米）
频数
频率
[3.0，5.0）

0.10
[5.0，7.0）

0.10
[7.0，9.0）

0.10
[9.0，11.0）

0.20
[11.0，13.0）

0.40
[13.0，15.0）
10

合计

1.00
（Ⅰ）求参加测试的男生中“优秀生”的人数；
（Ⅱ）从参加测试男生的成绩中，根据表中分组情况，按分层抽样的方法抽取10名男生的成绩作为一个样本，再从该样本中任选2名男生的成绩，求至少选出1名男生的成绩不低于13.0米的概率；
（Ⅲ）若将这次测试的频率作为概率，从该校全体男生中随机抽取3人，记X表示3人中“优秀生”的人数，求X的分布列及数学期望．

查看试题解析
17. 在四棱锥P﹣ABCD中，△PAD为正三角形，平面PAD⊥平面ABCD，E为AD的中点，AB∥CD，AB⊥AD，CD=2AB=2AD=4．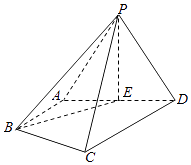
（Ⅰ）求证：平面PCD⊥平面PAD；
（Ⅱ）求直线PB与平面PCD所成角的正弦值；
（Ⅲ）在棱CD上是否存在点M，使得AM⊥平面PBE？若存在，求出 $\frac{D M}{D C}$ 的值；若不存在，说明理由．

查看试题解析
18. 设函数f（x）=a（x﹣1）²﹣xe²^﹣x ．
（Ⅰ）若曲线y=f（x）在点（2，f（2））处的切线与x轴平行，求a的值；
（Ⅱ）若 $a > - \frac{e}{2}$ ，求f（x）的单调区间．

查看试题解析
19. 已知椭圆E： $\frac{x^{2}}{a^{2}}$ + $\frac{y^{2}}{b^{2}}$ =1（a＞b＞0）的离心率为 $\frac{\sqrt{3}}{2}$ ，四边形ABCD的各顶点均在椭圆E上，且对角线AC，BD均过坐标原点O，点D（2，1），AC，BD的斜率之积为 $- \frac{1}{4}$ ．
（Ⅰ）求椭圆E的方程；
（Ⅱ）过D作直线l平行于AC．若直线l′平行于BD，且与椭圆E交于不同的两点M．N，与直线l交于点P．
⑴证明：直线l与椭圆E有且只有一个公共点；
⑵证明：存在常数λ，使得|PD|²=λ|PM|•|PN|，并求出λ的值．

查看试题解析
20. 设集合U={1，2，…，100}，T⊆U．对数列{a_n}（n∈N^*），规定：
①若T=∅，则S_T=0；
②若T={n₁ ， n₂ ， …，n_k}，则S_T=a $_{n_{1}}$ +a $_{n_{2}}$ +…+a $_{n_{k}}$ ．
例如：当a_n=2n，T={1，3，5}时，S_T=a₁+a₃+a₅=2+6+10=18．
已知等比数列{a_n}（n∈N^*），a₁=1，且当T={2，3}时，S_T=12，求数列{a_n}的通项公式．

查看试题解析

分组（米）	频数	频率
[3.0，5.0）		0.10
[5.0，7.0）		0.10
[7.0，9.0）		0.10
[9.0，11.0）		0.20
[11.0，13.0）		0.40
[13.0，15.0）	10
合计		1.00