2017年山东省淄博市中考数学试卷
试卷日期:2017-10-10 考试类型:中考真卷
一、选择题
-
1. ﹣ 的相反数是( )A、 B、 C、 D、﹣2. C919大飞机是中国完全具有自主知识产权的干线民用飞机,其零部件总数超过100万个,请将100万用科学记数法表示为( )A、1×106 B、100×104 C、1×107 D、0.1×1083. 下列几何体中,其主视图为三角形的是( )A、
 B、
B、 C、
C、 D、
D、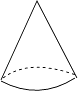 4. 下列运算正确的是( )A、a2•a3=a6 B、(﹣a2)3=﹣a5 C、a10÷a9=a(a≠0) D、(﹣bc)4÷(﹣bc)2=﹣b2c25. 若分式 的值为零,则x的值是( )A、1 B、﹣1 C、±1 D、26. 若a+b=3,a2+b2=7,则ab等于( )A、2 B、1 C、﹣2 D、﹣17. 将二次函数y=x2+2x﹣1的图象沿x轴向右平移2个单位长度,得到的函数表达式是( )
4. 下列运算正确的是( )A、a2•a3=a6 B、(﹣a2)3=﹣a5 C、a10÷a9=a(a≠0) D、(﹣bc)4÷(﹣bc)2=﹣b2c25. 若分式 的值为零,则x的值是( )A、1 B、﹣1 C、±1 D、26. 若a+b=3,a2+b2=7,则ab等于( )A、2 B、1 C、﹣2 D、﹣17. 将二次函数y=x2+2x﹣1的图象沿x轴向右平移2个单位长度,得到的函数表达式是( )
A、y=(x+3)2﹣2 B、y=(x+3)2+2 C、y=(x﹣1)2+2 D、y=(x﹣1)2﹣28. 若关于x的一元二次方程kx2﹣2x﹣1=0有两个不相等的实数根,则实数k的取值范围是( )A、k>﹣1 B、k>﹣1且k≠0 C、k<﹣1 D、k<﹣1或k=09. 如图,半圆的直径BC恰与等腰直角三角形ABC的一条直角边完全重合.若BC=4,则图中阴影部分的面积是( )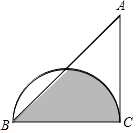 A、2+π B、2+2π C、4+π D、2+4π10. 在一个不透明的袋子里装有四个小球,球上分别标有6,7,8,9四个数字,这些小球除数字外都相同.甲、乙两人玩“猜数字”游戏,甲先从袋中任意摸出一个小球,将小球上的数字记为m,再由乙猜这个小球上的数字,记为n.如果m,n满足|m﹣n|≤1,那么就称甲、乙两人“心领神会”,则两人“心领神会”的概率是( )A、 B、 C、 D、11. 小明做了一个数学实验:将一个圆柱形的空玻璃杯放入形状相同的无水鱼缸内,看作一个容器.然后,小明对准玻璃杯口匀速注水,如图所示,在注水过程中,杯底始终紧贴鱼缸底部,则下面可以近似地刻画出容器最高水位h与注水时间t之间的变化情况的是( )
A、2+π B、2+2π C、4+π D、2+4π10. 在一个不透明的袋子里装有四个小球,球上分别标有6,7,8,9四个数字,这些小球除数字外都相同.甲、乙两人玩“猜数字”游戏,甲先从袋中任意摸出一个小球,将小球上的数字记为m,再由乙猜这个小球上的数字,记为n.如果m,n满足|m﹣n|≤1,那么就称甲、乙两人“心领神会”,则两人“心领神会”的概率是( )A、 B、 C、 D、11. 小明做了一个数学实验:将一个圆柱形的空玻璃杯放入形状相同的无水鱼缸内,看作一个容器.然后,小明对准玻璃杯口匀速注水,如图所示,在注水过程中,杯底始终紧贴鱼缸底部,则下面可以近似地刻画出容器最高水位h与注水时间t之间的变化情况的是( )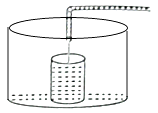 A、
A、 B、
B、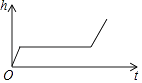 C、
C、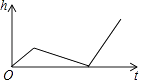 D、
D、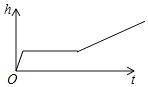 12. 如图,在Rt△ABC中,∠ABC=90°,AB=6,BC=8,∠BAC,∠ACB的平分线相交于点E,过点E作EF∥BC交AC于点F,则EF的长为( )
12. 如图,在Rt△ABC中,∠ABC=90°,AB=6,BC=8,∠BAC,∠ACB的平分线相交于点E,过点E作EF∥BC交AC于点F,则EF的长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 分解因式:2x3﹣8x= .14. 已知α,β是方程x2﹣3x﹣4=0的两个实数根,则α2+αβ﹣3α的值为 .15. 运用科学计算器(如图是其面板的部分截图)进行计算,按键顺序如下:
则计算器显示的结果是 .
16. 在边长为4的等边三角形ABC中,D为BC边上的任意一点,过点D分别作DE⊥AB,DF⊥AC,垂足分别为E,F,则DE+DF= .17. 设△ABC的面积为1.如图1,分别将AC,BC边2等分,D1 , E1是其分点,连接AE1 , BD1交于点F1 , 得到四边形CD1F1E1 , 其面积S1= .
如图2,分别将AC,BC边3等分,D1 , D2 , E1 , E2是其分点,连接AE2 , BD2交于点F2 , 得到四边形CD2F2E2 , 其面积S2= ;
如图3,分别将AC,BC边4等分,D1 , D2 , D3 , E1 , E2 , E3是其分点,连接AE3 , BD3交于点F3 , 得到四边形CD3F3E3 , 其面积S3= ;
…
按照这个规律进行下去,若分别将AC,BC边(n+1)等分,…,得到四边形CDnFnEn , 其面积Sn= .

三、解答题
-
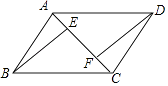
18. 解不等式: ≤ .19. 已知:如图,E,F为▱ABCD对角线AC上的两点,且AE=CF,连接BE,DF,求证:BE=DF.
 20. 某内陆城市为了落实国家“一带一路”倡议,促进经济发展,增强对外贸易的竞争力,把距离港口420km的普通公路升级成了同等长度的高速公路,结果汽车行驶的平均速度比原来提高了50%,行驶时间缩短了2h,求汽车原来的平均速度.21. 为了“天更蓝,水更绿”某市政府加大了对空气污染的治理力度,经过几年的努力,空气质量明显改善,现收集了该市连续30天的空气质量情况作为样本,整理并制作了如下表格和一幅不完整的条形统计图:
20. 某内陆城市为了落实国家“一带一路”倡议,促进经济发展,增强对外贸易的竞争力,把距离港口420km的普通公路升级成了同等长度的高速公路,结果汽车行驶的平均速度比原来提高了50%,行驶时间缩短了2h,求汽车原来的平均速度.21. 为了“天更蓝,水更绿”某市政府加大了对空气污染的治理力度,经过几年的努力,空气质量明显改善,现收集了该市连续30天的空气质量情况作为样本,整理并制作了如下表格和一幅不完整的条形统计图:空气污染指数(ω)
30
40
70
80
90
110
120
140
天数(t)
1
2
3
5
7
6
4
2
说明:环境空气质量指数(AQI)技术规定:ω≤50时,空气质量为优;51≤ω≤100时,空气质量为良;101≤ω≤150时,空气质量为轻度污染;151≤ω≤200时,空气质量为中度污染,…
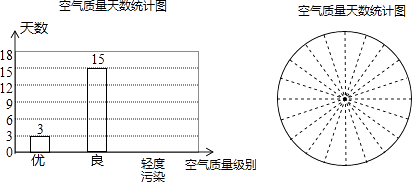
根据上述信息,解答下列问题:
(1)、直接写出空气污染指数这组数据的众数 , 中位数;(2)、请补全空气质量天数条形统计图;(3)、根据已完成的条形统计图,制作相应的扇形统计图;(4)、健康专家温馨提示:空气污染指数在100以下适合做户外运动.请根据以上信息,估计该市居民一年(以365天计)中有多少天适合做户外运动?22. 如图,在直角坐标系中,Rt△ABC的直角边AC在x轴上,∠ACB=90°,AC=1,反比例函数y= (k>0)的图象经过BC边的中点D(3,1).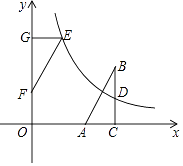 (1)、求这个反比例函数的表达式;(2)、若△ABC与△EFG成中心对称,且△EFG的边FG在y轴的正半轴上,点E在这个函数的图象上.
(1)、求这个反比例函数的表达式;(2)、若△ABC与△EFG成中心对称,且△EFG的边FG在y轴的正半轴上,点E在这个函数的图象上.①求OF的长;
②连接AF,BE,证明四边形ABEF是正方形.
23. 如图,将矩形纸片ABCD沿直线MN折叠,顶点B恰好与CD边上的动点P重合(点P不与点C,D重合),折痕为MN,点M,N分别在边AD,BC上,连接MB,MP,BP,BP与MN相交于点F.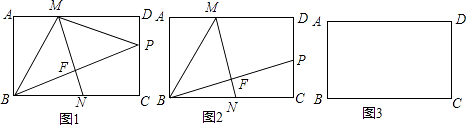 (1)、求证:△BFN∽△BCP;(2)、①在图2中,作出经过M,D,P三点的⊙O(要求保留作图痕迹,不写做法);
(1)、求证:△BFN∽△BCP;(2)、①在图2中,作出经过M,D,P三点的⊙O(要求保留作图痕迹,不写做法);②设AB=4,随着点P在CD上的运动,若①中的⊙O恰好与BM,BC同时相切,求此时DP的长.
24. 如图1,经过原点O的抛物线y=ax2+bx(a≠0)与x轴交于另一点A( ,0),在第一象限内与直线y=x交于点B(2,t).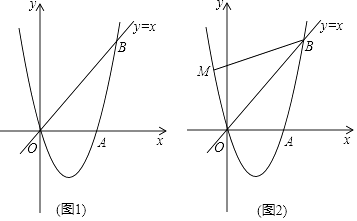 (1)、求这条抛物线的表达式;(2)、在第四象限内的抛物线上有一点C,满足以B,O,C为顶点的三角形的面积为2,求点C的坐标;(3)、如图2,若点M在这条抛物线上,且∠MBO=∠ABO,在(2)的条件下,是否存在点P,使得△POC∽△MOB?若存在,求出点P的坐标;若不存在,请说明理由.
(1)、求这条抛物线的表达式;(2)、在第四象限内的抛物线上有一点C,满足以B,O,C为顶点的三角形的面积为2,求点C的坐标;(3)、如图2,若点M在这条抛物线上,且∠MBO=∠ABO,在(2)的条件下,是否存在点P,使得△POC∽△MOB?若存在,求出点P的坐标;若不存在,请说明理由.