2017年江苏省镇江市中考数学试卷

试卷日期：2017-10-10 考试类型：中考真卷

前去【出卷网】下载

一、填空题

1. 3的倒数是．

查看试题解析
2. 计算：a⁵÷a³= ．

查看试题解析
3. 分解因式：9﹣b²= ．

查看试题解析
4. 当x=时，分式 $\frac{x - 5}{2 x + 3}$ 的值为零．

查看试题解析
5. 如图，转盘中6个扇形的面积都相等，任意转动转盘一次，当转盘停止转动时，指针指向奇数的概率是．

查看试题解析
6. 圆锥底面圆的半径为2，母线长为5，它的侧面积等于（结果保留π）．

查看试题解析
7. 如图，Rt△ABC中，∠ACB=90°，AB=6，点D是AB的中点，过AC的中点E作EF∥CD交AB于点F，则EF= ．

查看试题解析
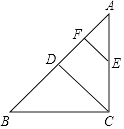8. 若二次函数y=x²﹣4x+n的图象与x轴只有一个公共点，则实数n= ．

查看试题解析
9. 如图，AB是⊙O的直径，AC与⊙O相切，CO交⊙O于点D．若∠CAD=30°，则∠BOD=°．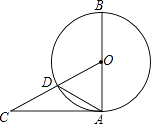

查看试题解析
10. 若实数a满足|a﹣ $\frac{1}{2}$ |= $\frac{3}{2}$ ，则a对应于图中数轴上的点可以是A，B，C三点中的点．

查看试题解析
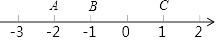11. 如图，△ABC中，AB=6，DE∥AC，将△BDE绕点B顺时针旋转得到△BD′E′，点D的对应点D′落在边BC上．已知BE′=5，D′C=4，则BC的长为．

查看试题解析
12. 已知实数m满足m²﹣3m+1=0，则代数式m²+ $\frac{19}{m^{2} + 2}$ 的值等于．

查看试题解析

二、选择题

13. 我国对“一带一路”沿线国家不断加大投资，目前已为有关国家创造了近1100000000美元税收，其中1100000000用科学记数法表示应为（）

A、0.11×10⁸ B、1.1×10⁹ C、1.1×10¹⁰ D、11×10⁸

查看试题解析
14. 如图是由6个大小相同的小正方体组成的几何体，它的主视图是（）

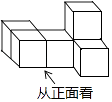A、 B、 C、 D、

查看试题解析
15. a、b是实数，点A（2，a）、B（3，b）在反比例函数y=﹣ $\frac{2}{x}$ 的图象上，则（）

A、a＜b＜0 B、b＜a＜0 C、a＜0＜b D、b＜0＜a

查看试题解析
16. 根据下表中的信息解决问题：
数据
37
38
39
40
41
频数
8
4
5
a
1
若该组数据的中位数不大于38，则符合条件的正整数a的取值共有（）

A、3个 B、4个 C、5个 D、6个

查看试题解析
17. 点E，F分别在平行四边形ABCD的边BC，AD上，BE=DF，点P在边AB上，AP：PB=1：n（n＞1），过点P且平行于AD的直线l将△ABE分成面积为S₁、S₂的两部分，将△CDF分成面积为S₃、S₄的两部分（如图），下列四个等式：
①S₁：S₃=1：n
②S₁：S₄=1：（2n+1）
③（S₁+S₄）：（S₂+S₃）=1：n
④（S₃﹣S₁）：（S₂﹣S₄）=n：（n+1）
其中成立的有（）

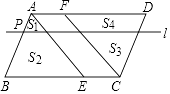A、①②④ B、②③ C、②③④ D、③④

查看试题解析

三、解答题

18. 计算题:

(1)、计算：（﹣2）²+tan45°﹣（ $\sqrt{3}$ ﹣2）⁰

(2)、化简：x（x+1）﹣（x+1）（x﹣2）

查看试题解析
19. 综合题:

(1)、解方程组： ${\begin{matrix} x - y = 4 \\ 2 x + y = 5 \end{matrix}$

(2)、解不等式： $\frac{x}{3}$ ＞1﹣ $\frac{x - 2}{2}$ ．

查看试题解析
20. 为了解射击运动员小杰的集训效果，教练统计了他集训前后的两次测试成绩（每次测试射击10次），制作了如图所示的条形统计图．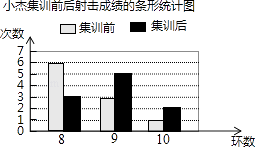

(1)、集训前小杰射击成绩的众数为；

(2)、分别计算小杰集训前后射击的平均成绩；

(3)、请用一句话评价小杰这次集训的效果．

查看试题解析
21. 某校5月份举行了八年级生物实验考查，有A和B两个考查实验，规定每位学生只参加其中一个实验的考查，并由学生自己抽签决定具体的考查实验，小明、小丽、小华都参加了本次考查．

(1)、小丽参加实验A考查的概率是；

(2)、用列表或画树状图的方法求小明、小丽都参加实验A考查的概率；

(3)、他们三人都参加实验A考查的概率是．

查看试题解析
22. 如图，点B，E分别在AC，DF上，AF分别交BD，CE于点M，N，∠A=∠F，∠1=∠2．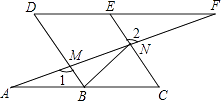

(1)、求证：四边形BCED是平行四边形；

(2)、已知DE=2，连接BN，若BN平分∠DBC，求CN的长．

查看试题解析
23. 如图，小明在教学楼A处分别观测对面实验楼CD底部的俯角为45°，顶部的仰角为37°，已知教学楼和实验楼在同一平面上，观测点距地面的垂直高度AB为15m，求实验楼的垂直高度即CD长（精确到1m）
参考值：sin37°=0.60，cos37°=0.80，tan37°=0.75．

查看试题解析
24. 如图，Rt△ABC中，∠B=90°，AB=3cm，BC=4cm．点D在AC上，AD=1cm，点P从点A出发，沿AB匀速运动；点Q从点C出发，沿C→B→A→C的路径匀速运动．两点同时出发，在B点处首次相遇后，点P的运动速度每秒提高了2cm，并沿B→C→A的路径匀速运动；点Q保持速度不变，并继续沿原路径匀速运动，两点在D点处再次相遇后停止运动，设点P原来的速度为xcm/s．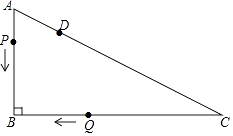

(1)、点Q的速度为cm/s（用含x的代数式表示）．

(2)、求点P原来的速度．

查看试题解析
25. 如图1，一次函数y=﹣x+b与反比例函数y= $\frac{k}{x}$ （k≠0）的图象交于点A（1，3），B（m，1），与x轴交于点D，直线OA与反比例函数y= $\frac{k}{x}$ （k≠0）的图象的另一支交于点C，过点B作直线l垂直于x轴，点E是点D关于直线l的对称点．

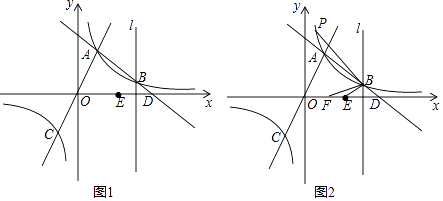(1)、k=；

(2)、判断点B，E，C是否在同一条直线上，并说明理由；

(3)、如图2，已知点F在x轴正半轴上，OF= $\frac{3}{2}$ ，点P是反比例函数y= $\frac{k}{x}$ （k≠0）的图象位于第一象限部分上的点（点P在点A的上方），∠ABP=∠EBF，则点P的坐标为（，）．

查看试题解析
26. 如图1，Rt△ACB 中，∠C=90°，点D在AC上，∠CBD=∠A，过A、D两点的圆的圆心O在AB上．

(1)、利用直尺和圆规在图1中画出⊙O（不写作法，保留作图痕迹，并用黑色水笔把线条描清楚）；

(2)、判断BD所在直线与（1）中所作的⊙O的位置关系，并证明你的结论；

(3)、设⊙O交AB于点E，连接DE，过点E作EF⊥BC，F为垂足，若点D是线段AC的黄金分割点（即 $\frac{D C}{A D}$ = $\frac{A D}{A C}$ ），如图2，试说明四边形DEFC是正方形）．

查看试题解析
27. 如图，在平面直角坐标系中，矩形OABC的边OA，OC分别在x轴、y轴上，点B坐标为（4，t）（t＞0），二次函数y=x²+bx（b＜0）的图象经过点B，顶点为点D．

(1)、当t=12时，顶点D到x轴的距离等于；

(2)、点E是二次函数y=x²+bx（b＜0）的图象与x轴的一个公共点（点E与点O不重合），求OE•EA的最大值及取得最大值时的二次函数表达式；

(3)、矩形OABC的对角线OB、AC交于点F，直线l平行于x轴，交二次函数y=x²+bx（b＜0）的图象于点M、N，连接DM、DN，当△DMN≌△FOC时，求t的值．

查看试题解析
28.

(1)、【回顾】
如图1，△ABC中，∠B=30°，AB=3，BC=4，则△ABC的面积等于．

(2)、【探究】
图2是同学们熟悉的一副三角尺，一个含有30°的角，较短的直角边长为a；另一个含有45°的角，直角边长为b，小明用两副这样的三角尺拼成一个平行四边形ABCD（如图3），用了两种不同的方法计算它的面积，从而推出sin75°= $\frac{\sqrt{6} + \sqrt{2}}{4}$ ，小丽用两副这样的三角尺拼成了一个矩形EFGH（如图4），也推出sin75°= $\frac{\sqrt{6} + \sqrt{2}}{4}$ ，请你写出小明或小丽推出sin75°= $\frac{\sqrt{6} + \sqrt{2}}{4}$ 的具体说理过程．

(3)、【应用】
在四边形ABCD中，AD∥BC，∠D=75°，BC=6，CD=5，AD=10（如图5）
①点E在AD上，设t=BE+CE，求t²的最小值；
②点F在AB上，将△BCF沿CF翻折，点B落在AD上的点G处，点G是AD的中点吗？说明理由．

查看试题解析

数据	37	38	39	40	41
频数	8	4	5	a	1