2017年江苏省泰州市中考数学试卷

试卷日期：2017-10-10 考试类型：中考真卷

前去【出卷网】下载

一、选择题

1. 2的算术平方根是（）

A、 $\pm \sqrt{2}$ B、 $\sqrt{2}$ C、 $- \sqrt{2}$ D、2

查看试题解析
2. 下列运算正确的是（）

A、a³•a³=2a⁶ B、a³+a³=2a⁶ C、（a³）²=a⁶ D、a⁶•a²=a³

查看试题解析
3. 把下列英文字母看成图形，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 三角形的重心是（）

A、三角形三条边上中线的交点 B、三角形三条边上高线的交点 C、三角形三条边垂直平分线的交点 D、三角形三条内角平分线的交点

查看试题解析
5. 某科普小组有5名成员，身高分别为（单位：cm）：160，165，170，163，167．增加1名身高为165cm的成员后，现科普小组成员的身高与原来相比，下列说法正确的是（）

A、平均数不变，方差不变 B、平均数不变，方差变大 C、平均数不变，方差变小 D、平均数变小，方差不变

查看试题解析
6. 如图，P为反比例函数y= $\frac{k}{x}$ （k＞0）在第一象限内图象上的一点，过点P分别作x轴，y轴的垂线交一次函数y=﹣x﹣4的图象于点A，B．若∠AOB=135°，则k的值是（）

A、2 B、4 C、6 D、8

查看试题解析

二、填空题

7. |﹣4|= ．

查看试题解析
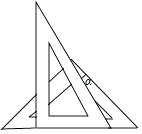
8. 天宫二号在太空绕地球一周大约飞行42500千米，将42500用科学记数法表示为．

查看试题解析
9. 已知2m﹣3n=﹣4，则代数式m（n﹣4）﹣n（m﹣6）的值为．

查看试题解析
10. “一只不透明的袋子共装有3个小球，它们的标号分别为1，2，3，从中摸出1个小球，标号为“4”，这个事件是．（填“必然事件”、“不可能事件”或“随机事件”）

查看试题解析
11. 将一副三角板如图叠放，则图中∠α的度数为．

查看试题解析
12. 扇形的半径为3cm，弧长为2πcm，则该扇形的面积为cm² ．

查看试题解析
13. 方程2x²+3x﹣1=0的两个根为x₁、x₂ ，则 $\frac{1}{x_{1}}$ + $\frac{1}{x_{2}}$ 的值等于．

查看试题解析
14. 小明沿着坡度i为1： $\sqrt{3}$ 的直路向上走了50m，则小明沿垂直方向升高了m．

查看试题解析
15. 如图，在平面直角坐标系xOy中，点A，B，P的坐标分别为（1，0），（2，5），（4，2）．若点C在第一象限内，且横坐标、纵坐标均为整数，P是△ABC的外心，则点C的坐标为．

查看试题解析
16. 如图，在平面内，线段AB=6，P为线段AB上的动点，三角形纸片CDE的边CD所在的直线与线段AB垂直相交于点P，且满足PC=PA．若点P沿AB方向从点A运动到点B，则点E运动的路径长为．

查看试题解析

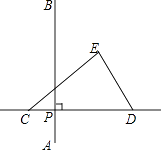
三、解答题

17. 计算题：

(1)、计算：（ $\sqrt{7}$ ﹣1）⁰﹣（﹣ $\frac{1}{2}$ ）^﹣²+ $\sqrt{3}$ tan30°；

(2)、解方程： $\frac{x + 1}{x - 1}$ + $\frac{4}{1 - x^{2}}$ =1．

查看试题解析
18. “泰微课”是学生自主学习的平台，某初级中学共有1200名学生，每人每周学习的数学泰微课都在6至30个之间（含6和30），为进一步了解该校学生每周学习数学泰微课的情况，从三个年级随机抽取了部分学生的相关学习数据，并整理、绘制成统计图如下：
根据以上信息完成下列问题：

(1)、补全条形统计图；

(2)、估计该校全体学生中每周学习数学泰微课在16至30个之间（含16和30）的人数．

查看试题解析
19. 在学校组织的朗诵比赛中，甲、乙两名学生以抽签的方式从3篇不同的文章中抽取一篇参加比赛，抽签规则是：在3个相同的标签上分别标注字母A、B、C，各代表1篇文章，一名学生随机抽取一个标签后放回，另一名学生再随机抽取．用画树状图或列表的方法列出所有等可能的结果，并求甲、乙抽中同一篇文章的概率．

查看试题解析
20. 如图，△ABC中，∠ACB＞∠ABC．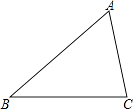

(1)、用直尺和圆规在∠ACB的内部作射线CM，使∠ACM=∠ABC（不要求写作法，保留作图痕迹）；

(2)、若（1）中的射线CM交AB于点D，AB=9，AC=6，求AD的长．

查看试题解析
21. 平面直角坐标系xOy中，点P的坐标为（m+1，m﹣1）．

(1)、试判断点P是否在一次函数y=x﹣2的图象上，并说明理由；

(2)、如图，一次函数y=﹣ $\frac{1}{2}$ x+3的图象与x轴、y轴分别相交于点A、B，若点P在△AOB的内部，求m的取值范围．

查看试题解析
22. 如图，正方形ABCD中，G为BC边上一点，BE⊥AG于E，DF⊥AG于F，连接DE．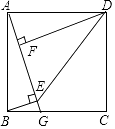

(1)、求证：△ABE≌△DAF；

(2)、若AF=1，四边形ABED的面积为6，求EF的长．

查看试题解析
23. 怡然美食店的A，B两种菜品，每份成本均为14元，售价分别为20元、18元，这两种菜品每天的营业额共为1120元，总利润为280元．

(1)、该店每天卖出这两种菜品共多少份？

(2)、该店为了增加利润，准备降低A种菜品的售价，同时提高B种菜品的售价，售卖时发现，A种菜品售价每降0.5元可多卖1份；B种菜品售价每提高0.5元就少卖1份，如果这两种菜品每天销售总份数不变，那么这两种菜品一天的总利润最多是多少？

查看试题解析
24. 如图，⊙O的直径AB=12cm，C为AB延长线上一点，CP与⊙O相切于点P，过点B作弦BD∥CP，连接PD．

(1)、求证：点P为 $\hat{B D}$ 的中点；

(2)、若∠C=∠D，求四边形BCPD的面积．

查看试题解析
25. 阅读理解：
如图①，图形l外一点P与图形l上各点连接的所有线段中，若线段PA₁最短，则线段PA₁的长度称为点P到图形l的距离．
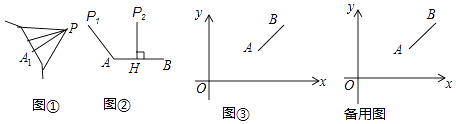
例如：图②中，线段P₁A的长度是点P₁到线段AB的距离；线段P₂H的长度是点P₂到线段AB的距离．
解决问题：
如图③，平面直角坐标系xOy中，点A、B的坐标分别为（8，4），（12，7），点P从原点O出发，以每秒1个单位长度的速度向x轴正方向运动了t秒．

(1)、当t=4时，求点P到线段AB的距离；

(2)、t为何值时，点P到线段AB的距离为5？

(3)、t满足什么条件时，点P到线段AB的距离不超过6？（直接写出此小题的结果）

查看试题解析
26. 平面直角坐标系xOy中，点A，B的横坐标分别为a、a+2，二次函数y=﹣x²+（m﹣2）x+2m的图象经过点A，B，且a、m满足2a﹣m=d（d为常数）．

(1)、若一次函数y₁=kx+b的图象经过A、B两点．
①当a=1、d=﹣1时，求k的值；
②若y₁随x的增大而减小，求d的取值范围；

(2)、当d=﹣4且a≠﹣2、a≠﹣4时，判断直线AB与x轴的位置关系，并说明理由；

(3)、点A，B的位置随着a的变化而变化，设点A，B运动的路线与y轴分别相交于点C，D，线段CD的长度会发生变化吗？如果不变，求出CD的长；如果变化，请说明理由．

查看试题解析