2017年湖南省永州市中考数学试卷
试卷日期:2017-09-30 考试类型:中考真卷
一、选择题
-
1. ﹣8的绝对值是( )A、8 B、﹣8 C、 D、﹣2. x=1是关于x的方程2x﹣a=0的解,则a的值是( )A、﹣2 B、2 C、﹣1 D、13. 江永女书诞生于宋朝,是世界上唯一一种女性文字,主要书写在精制布面、扇面、布帕等物品上,是一种独特而神奇的文化现象.下列四个文字依次为某女书传人书写的“女书文化”四个字,基本是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 下列运算正确的是( )A、a•a2=a2 B、(ab)2=ab C、3﹣1= D、5. 下面是某一天永州市11个旅游景区最高气温(单位:℃)的统计表:
4. 下列运算正确的是( )A、a•a2=a2 B、(ab)2=ab C、3﹣1= D、5. 下面是某一天永州市11个旅游景区最高气温(单位:℃)的统计表:景区
潇水湖
东山景区
浯溪碑林
舜皇山
阳明山
鬼崽岭
九嶷山
上甘棠
涔天河
湘江源
南武当
气温
31
30
31
25
28
27
26
28
28
25
29
则下列说法正确的是( )
A、该组数据的方差为0 B、该组数据的平均数为25 C、该组数据的中位数为27 D、该组数据的众数为286. 湖南省第二次文物普查时,省考古研究所在冷水滩钱家州征集到一个宋代“青釉瓜棱形瓷执壶”如图所示,该壶为盛酒器,瓷质,侈口,喇叭形长颈,长立把,则该“青釉瓜棱形瓷执壶”的主视图是( ) A、
A、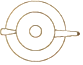 B、
B、 C、
C、 D、
D、 7. 小红不小心把家里的一块圆形玻璃打碎了,需要配制一块同样大小的玻璃镜,工人师傅在一块如图所示的玻璃镜残片的边缘描出了点A,B,C,给出三角形ABC,则这块玻璃镜的圆心是( )
7. 小红不小心把家里的一块圆形玻璃打碎了,需要配制一块同样大小的玻璃镜,工人师傅在一块如图所示的玻璃镜残片的边缘描出了点A,B,C,给出三角形ABC,则这块玻璃镜的圆心是( )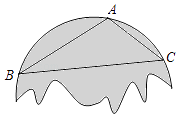 A、AB,AC边上的中线的交点 B、AB,AC边上的垂直平分线的交点 C、AB,AC边上的高所在直线的交点 D、∠BAC与∠ABC的角平分线的交点8. 如图,在△ABC中,点D是AB边上的一点,若∠ACD=∠B,AD=1,AC=2,△ADC的面积为1,则△BCD的面积为( )
A、AB,AC边上的中线的交点 B、AB,AC边上的垂直平分线的交点 C、AB,AC边上的高所在直线的交点 D、∠BAC与∠ABC的角平分线的交点8. 如图,在△ABC中,点D是AB边上的一点,若∠ACD=∠B,AD=1,AC=2,△ADC的面积为1,则△BCD的面积为( )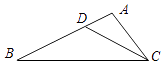 A、1 B、2 C、3 D、49. 在同一平面直角坐标系中,函数y=x+k与y= (k为常数,k≠0)的图象大致是( )A、
A、1 B、2 C、3 D、49. 在同一平面直角坐标系中,函数y=x+k与y= (k为常数,k≠0)的图象大致是( )A、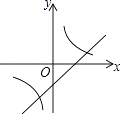 B、
B、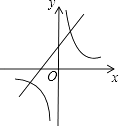 C、
C、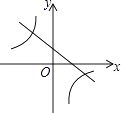 D、
D、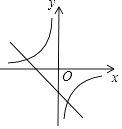 10. 已知从n个人中,选出m个人按照一定的顺序排成一行,所有不同的站位方法有n×(n﹣1)×…×(n﹣m+1)种.现某校九年级甲、乙、丙、丁4名同学和1位老师共5人在毕业前合影留念(站成一行).若老师站在中间,则不同的站位方法有( )A、6种 B、20种 C、24种 D、120种
10. 已知从n个人中,选出m个人按照一定的顺序排成一行,所有不同的站位方法有n×(n﹣1)×…×(n﹣m+1)种.现某校九年级甲、乙、丙、丁4名同学和1位老师共5人在毕业前合影留念(站成一行).若老师站在中间,则不同的站位方法有( )A、6种 B、20种 C、24种 D、120种二、填空题
-
11. 2017年端午小长假的第一天,永州市共接待旅客约275 000人次,请将275 000用科学记数法表示为 .12. 满足不等式组 的整数解是 .13. 某水果店搞促销活动,对某种水果打8折出售,若用60元钱买这种水果,可以比打折前多买3斤.设该种水果打折前的单价为x元,根据题意可列方程为 .
14. 把分别写有数字1,2,3,4,5的5张同样的小卡片放进不透明的盒子里,搅拌均匀后随机取出一张小卡片,则取出的卡片上的数字大于3的概率是 .15. 如图,已知反比例函数y= (k为常数,k≠0)的图象经过点A,过A点作AB⊥x轴,垂足为B.若△AOB的面积为1,则k= .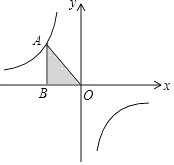 16. 如图,四边形ABCD是⊙O的内接四边形,点D是 的中点,点E是 上的一点,若∠CED=40°,则∠ADC=度.
16. 如图,四边形ABCD是⊙O的内接四边形,点D是 的中点,点E是 上的一点,若∠CED=40°,则∠ADC=度.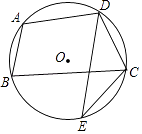 17. 如图,这是某同学用纸板做成的一个底面直径为10cm,高为12cm的无底圆锥形玩具(接缝忽略不计),则做这个玩具所需纸板的面积是cm2(结果保留π).
17. 如图,这是某同学用纸板做成的一个底面直径为10cm,高为12cm的无底圆锥形玩具(接缝忽略不计),则做这个玩具所需纸板的面积是cm2(结果保留π). 18. 一小球从距地面1m高处自由落下,每次着地后又跳回到原高度的一半再落下.(1)、小球第3次着地时,经过的总路程为m;(2)、小球第n次着地时,经过的总路程为m.
18. 一小球从距地面1m高处自由落下,每次着地后又跳回到原高度的一半再落下.(1)、小球第3次着地时,经过的总路程为m;(2)、小球第n次着地时,经过的总路程为m.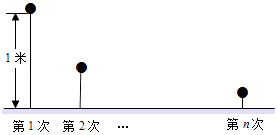
三、解答题
-
19. 计算: cos45°+(π﹣2017)0﹣ .20. 先化简,再求值:( + )÷ .其中x是0,1,2这三个数中合适的数.21. 某校组织了一次防溺水、防交通事故、防食物中毒、防校园欺凌及其他各种安全意识的调查活动,了解同学们在哪些方面的安全意识薄弱,便于今后更好地开展安全教育活动.根据调查结果,绘制出图1,图2两幅不完整的统计图.
请结合图中的信息解答下列问题:
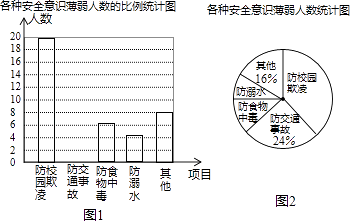 (1)、本次调查的人数为 , 其中防校园欺凌意识薄弱的人数占%;(2)、补全条形统计图;(3)、若该校共有1500名学生,请估计该校学生中防溺水意识薄弱的人数;(4)、请你根据题中的信息,给该校的安全教育提一个合理的建议.22. 如图,已知四边形ABCD是菱形,DF⊥AB于点F,BE⊥CD于点E.
(1)、本次调查的人数为 , 其中防校园欺凌意识薄弱的人数占%;(2)、补全条形统计图;(3)、若该校共有1500名学生,请估计该校学生中防溺水意识薄弱的人数;(4)、请你根据题中的信息,给该校的安全教育提一个合理的建议.22. 如图,已知四边形ABCD是菱形,DF⊥AB于点F,BE⊥CD于点E. (1)、求证:AF=CE;(2)、若DE=2,BE=4,求sin∠DAF的值.
(1)、求证:AF=CE;(2)、若DE=2,BE=4,求sin∠DAF的值.
23. 永州市是一个降水丰富的地区,今年4月初,某地连续降雨导致该地某水库水位持续上涨,下表是该水库4月1日~4月4日的水位变化情况:日期x
1
2
3
4
水位y(米)
20.00
20.50
21.00
21.50
(1)、请建立该水库水位y与日期x之间的函数模型;(2)、请用求出的函数表达式预测该水库今年4月6日的水位;(3)、你能用求出的函数表达式预测该水库今年12月1日的水位吗?24. 如图,已知AB是⊙O的直径,过O点作OP⊥AB,交弦AC于点D,交⊙O于点E,且使∠PCA=∠ABC. (1)、求证:PC是⊙O的切线;(2)、若∠P=60°,PC=2,求PE的长.25. 如图,已知抛物线y=ax2+bx+1经过A(﹣1,0),B(1,1)两点.
(1)、求证:PC是⊙O的切线;(2)、若∠P=60°,PC=2,求PE的长.25. 如图,已知抛物线y=ax2+bx+1经过A(﹣1,0),B(1,1)两点.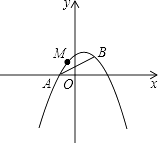 (1)、求该抛物线的解析式;(2)、阅读理解:
(1)、求该抛物线的解析式;(2)、阅读理解:在同一平面直角坐标系中,直线l1:y=k1x+b1(k1 , b1为常数,且k1≠0),直线l2:y=k2x+b2(k2 , b2为常数,且k2≠0),若l1⊥l2 , 则k1•k2=﹣1.
解决问题:
①若直线y=3x﹣1与直线y=mx+2互相垂直,求m的值;
②抛物线上是否存在点P,使得△PAB是以AB为直角边的直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)、M是抛物线上一动点,且在直线AB的上方(不与A,B重合),求点M到直线AB的距离的最大值.26. 已知点O是正方形ABCD对角线BD的中点.(1)、如图1,若点E是OD的中点,点F是AB上一点,且使得∠CEF=90°,过点E作ME∥AD,交AB于点M,交CD于点N.
①∠AEM=∠FEM; ②点F是AB的中点;
(2)、如图2,若点E是OD上一点,点F是AB上一点,且使 = = ,请判断△EFC的形状,并说明理由;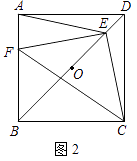 (3)、如图3,若E是OD上的动点(不与O,D重合),连接CE,过E点作EF⊥CE,交AB于点F,当 = 时,请猜想 的值(请直接写出结论).
(3)、如图3,若E是OD上的动点(不与O,D重合),连接CE,过E点作EF⊥CE,交AB于点F,当 = 时,请猜想 的值(请直接写出结论).