广西贵港市港南区2016-2017学年七年级下学期数学期末考试试卷
试卷日期:2017-09-21 考试类型:期末考试
一、选择题
-
1. 下列轴对称图形中,对称轴条数是四条的图形是( )A、
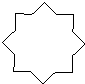 B、
B、 C、
C、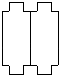 D、
D、 2. 下列等式中,正确的是( )A、3a﹣2a=1 B、a2•a3=a5 C、(﹣2a3)2=﹣4a6 D、(a﹣b)2=a2﹣b23. 下列因式分解正确的是( )A、x2﹣4=(x+4)(x﹣4) B、x2+2x+1=x(x+2)+1 C、3mx﹣6my=3m(x﹣6y) D、2x+4=2(x+2)4. 某班开展1分钟仰卧起坐比赛活动,5名同学的成绩如下(单位:个):37、38、40、40、42.这组数据的众数是( )A、37 B、38 C、40 D、425. 如果(x﹣2)(x+3)=x2+px+q,那么p、q的值为( )A、p=5,q=6 B、p=﹣1,q=6 C、p=1,q=﹣6 D、p=5,q=﹣66. 方程组 的解是( )A、 B、 C、 D、7. 为了开展阳光体育活动,某班计划购买毽子和跳绳两种体育用品,共花费35元,毽子单价3元,跳绳单价5元,购买方案有( )A、1种 B、2种 C、3种 D、4种8. 下列说法正确的是( )A、相等的两个角是对顶角 B、同位角相等 C、图形平移后的大小可以发生改变 D、两条直线相交所成的四个角都相等,则这两条直线互相垂直9. 如图是小芹6月1日﹣7日每天的自主学习时间统计图,则小芹这七天平均每天的自主学习时间是( )
2. 下列等式中,正确的是( )A、3a﹣2a=1 B、a2•a3=a5 C、(﹣2a3)2=﹣4a6 D、(a﹣b)2=a2﹣b23. 下列因式分解正确的是( )A、x2﹣4=(x+4)(x﹣4) B、x2+2x+1=x(x+2)+1 C、3mx﹣6my=3m(x﹣6y) D、2x+4=2(x+2)4. 某班开展1分钟仰卧起坐比赛活动,5名同学的成绩如下(单位:个):37、38、40、40、42.这组数据的众数是( )A、37 B、38 C、40 D、425. 如果(x﹣2)(x+3)=x2+px+q,那么p、q的值为( )A、p=5,q=6 B、p=﹣1,q=6 C、p=1,q=﹣6 D、p=5,q=﹣66. 方程组 的解是( )A、 B、 C、 D、7. 为了开展阳光体育活动,某班计划购买毽子和跳绳两种体育用品,共花费35元,毽子单价3元,跳绳单价5元,购买方案有( )A、1种 B、2种 C、3种 D、4种8. 下列说法正确的是( )A、相等的两个角是对顶角 B、同位角相等 C、图形平移后的大小可以发生改变 D、两条直线相交所成的四个角都相等,则这两条直线互相垂直9. 如图是小芹6月1日﹣7日每天的自主学习时间统计图,则小芹这七天平均每天的自主学习时间是( )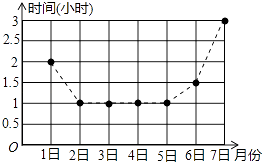 A、1小时 B、1.5小时 C、2小时 D、3小时10.
A、1小时 B、1.5小时 C、2小时 D、3小时10.如图,在△ABC中,点D、E、F分别是三条边上的点,EF∥AC,DF∥AB,∠B=45°,∠C=60°.则∠EFD=( )
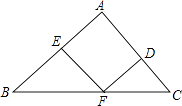 A、80° B、75° C、70° D、65°11.
A、80° B、75° C、70° D、65°11.如图,m∥n,直线l分别交m,n于点A,点B,AC⊥AB,AC交直线n于点C,若∠1=35°,则∠2等于( )
 A、35° B、45° C、55° D、65°12.
A、35° B、45° C、55° D、65°12.如图所示的直角三角形ABC向右翻滚,下列说法:(1)①到②是旋转;(2)①到③是平移;(3)①到④是平移;(4)②到③是旋转,其中正确的有( )
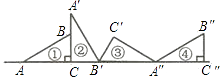 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 已知3a﹣2b=1,则9a﹣6b= .14. 在一次数学测验中,随机抽取了10份试卷,其成绩如下:85,81,89,81,72,82,77,81,79,83,则这组数据的中位数为 .15. 若|a﹣2|+(b+0.5)2=0,则(a•b)2017= .16. 若a2﹣b2= ,a﹣b= ,则a+b的值为 .17. 由方程组 ,可得到x与y的关系式是 .18. 任何一个正整数n都可以写成两个正整数相乘的形式,对于两个因数的差的绝对值最小的一种分解a=m×n(m≤n)可称为正整数a的最佳分解,并记作F(a)= .如:12=1×12=2×6=3×4,则F(12)= .则在以下结论:①F(5)=5;②F(24)= ;③若a是一个完全平方数,则F(a)=1;
④若a是一个完全立方数,即a=x3(x是正整数),则F(a)=x.则正确的结论有(填序号)
三、解答题
-
19. 综合题(1)、因式分解:4x2﹣16(2)、解方程组 .20. 已知实数a、b满足ab=1,a+b=2,求代数式a2b+ab2的值.21. 如图,已知AB∥CD,∠B=65°,CM平分∠BCE,∠MCN=90°,求∠DCN的度数.
 22. 我市某中学举行“中国梦•校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.
22. 我市某中学举行“中国梦•校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.平均分(分)
中位数(分)
众数(分)
初中部
85
高中部
85
100
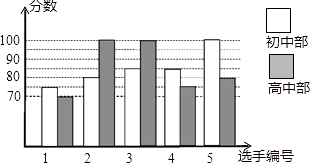 (1)、根据图示填写表;(2)、结合两队成绩的平均数和中位数进行分析,哪个队的决赛成绩较好?(3)、计算两队决赛成绩的方差,并判断哪一个代表队选手成绩较为稳定.23. 今年海南西瓜收成良好,小华家也喜获丰收,小华家今年种植“黑美人”西瓜5亩,“无籽”西瓜20亩,共收70000千克,按市场价“黑美人”每千克2.4元,“无籽”西瓜每千克4元出售,收入264000元.(1)、小华家今年种植的“黑美人”西瓜和“无籽”西瓜亩产各多少千克?(2)、如果知道种植1亩“黑美人”西瓜的成本为3000元,1亩“无籽”西瓜的成本为4000元,小华家今年种植西瓜共赚了多少钱?24. 将方格纸中的三角形ABC先向右平移2格得到三角形DEF,再将三角形DEF向上平移3格得到三角形GPH.
(1)、根据图示填写表;(2)、结合两队成绩的平均数和中位数进行分析,哪个队的决赛成绩较好?(3)、计算两队决赛成绩的方差,并判断哪一个代表队选手成绩较为稳定.23. 今年海南西瓜收成良好,小华家也喜获丰收,小华家今年种植“黑美人”西瓜5亩,“无籽”西瓜20亩,共收70000千克,按市场价“黑美人”每千克2.4元,“无籽”西瓜每千克4元出售,收入264000元.(1)、小华家今年种植的“黑美人”西瓜和“无籽”西瓜亩产各多少千克?(2)、如果知道种植1亩“黑美人”西瓜的成本为3000元,1亩“无籽”西瓜的成本为4000元,小华家今年种植西瓜共赚了多少钱?24. 将方格纸中的三角形ABC先向右平移2格得到三角形DEF,再将三角形DEF向上平移3格得到三角形GPH.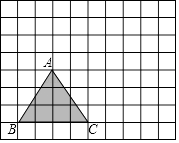 (1)、作图(不要求写作法):按上面步骤作出经过两次平移后分别得到的三角形;(2)、填空:图中与AC既平行又相等的线段有 , 图中有个平行四边形?(3)、线段AD与BF是什么位置关系和数量关系?25. 如图,直线EF,CD相交于点0,OA⊥OB,且OC平分∠AOF,
(1)、作图(不要求写作法):按上面步骤作出经过两次平移后分别得到的三角形;(2)、填空:图中与AC既平行又相等的线段有 , 图中有个平行四边形?(3)、线段AD与BF是什么位置关系和数量关系?25. 如图,直线EF,CD相交于点0,OA⊥OB,且OC平分∠AOF,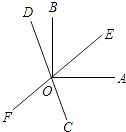 (1)、若∠AOE=40°,求∠BOD的度数;(2)、若∠AOE=α,求∠BOD的度数;(用含α的代数式表示)(3)、从(1)(2)的结果中能看出∠AOE和∠BOD有何关系?26.
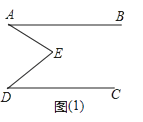
(1)、若∠AOE=40°,求∠BOD的度数;(2)、若∠AOE=α,求∠BOD的度数;(用含α的代数式表示)(3)、从(1)(2)的结果中能看出∠AOE和∠BOD有何关系?26.如图(1),E是直线AB,CD内部一点,AB∥CD,连接EA,ED.
 (1)、探究:
(1)、探究:①若∠A=30°,∠D=40°,则∠AED等于多少度?
②若∠A=20°,∠D=60°,则∠AED等于多少度?
③在图(1)中∠AED、∠EAB、∠EDC有什么数量关系,并证明你的结论.
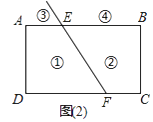
(2)、拓展:如图(2),射线FE与矩形ABCD的边AB交于点E,与边CD交于点F,①②③④分别是被射线FE隔开的四个区域(不含边界,其中③④位于直线AB的上方),P是位于以上四个区域上点,猜想:∠PEB、∠PFC、∠EPF之间的关系.(不要求证明)