陕西省咸阳市2016-2017学年高一上学期数学期末考试试卷
试卷日期:2017-09-16 考试类型:期末考试
一、选择题
-
1. 已知集合A={1,2,3},B={y|y=x﹣2,x∈A},则A∩B=( )A、{1} B、{4} C、{1,3} D、{1,4}2. 下列四条直线,倾斜角最大的是( )A、x=1 B、y=x+1 C、y=2x+1 D、y=﹣x+13. 如图,在正方体ABCD﹣A1B1C1D1中,直线BD与A1C1的位置关系是( )
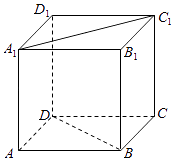 A、平行 B、相交 C、异面但不垂直 D、异面且垂直4. 函数y=f(x)和x=2的交点个数为( )A、0个 B、1个 C、2个 D、0个或1个5. 已知集合A={x|log2x>0},B={x|x<2},则( )A、A∩B=∅ B、A∪B=R C、B⊆A D、A⊆B6. 函数y=loga(x﹣1)(0<a<1)的图象大致是( )
A、平行 B、相交 C、异面但不垂直 D、异面且垂直4. 函数y=f(x)和x=2的交点个数为( )A、0个 B、1个 C、2个 D、0个或1个5. 已知集合A={x|log2x>0},B={x|x<2},则( )A、A∩B=∅ B、A∪B=R C、B⊆A D、A⊆B6. 函数y=loga(x﹣1)(0<a<1)的图象大致是( )
A、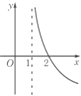 B、
B、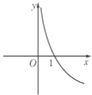 C、
C、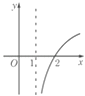 D、
D、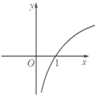 7. 已知两点P(4,0),Q(0,2),则以线段PQ为直径的圆的方程是( )A、(x+2)2+(y+1)2=5 B、(x﹣2)2+(y﹣1)2=10 C、(x﹣2)2+(y﹣1)2=5 D、(x+2)2+(y+1)2=108. 下列函数中,满足“对任意x1 , x2∈(0,+∞),当x1<x2时,都有f(x1)>f(x2)”的是( )A、f(x)=(x﹣1)2 B、f(x)= C、f(x)=ex D、f(x)=lnx9. 设a=( ) ,b=( ) ,c=log3 ,则a,b,c的大小关系是( )A、b<a<c B、c<b<a C、c<a<b D、b<c<a10. 若某空间几何体的三视图如图所示,则该几何体的表面积是( )
7. 已知两点P(4,0),Q(0,2),则以线段PQ为直径的圆的方程是( )A、(x+2)2+(y+1)2=5 B、(x﹣2)2+(y﹣1)2=10 C、(x﹣2)2+(y﹣1)2=5 D、(x+2)2+(y+1)2=108. 下列函数中,满足“对任意x1 , x2∈(0,+∞),当x1<x2时,都有f(x1)>f(x2)”的是( )A、f(x)=(x﹣1)2 B、f(x)= C、f(x)=ex D、f(x)=lnx9. 设a=( ) ,b=( ) ,c=log3 ,则a,b,c的大小关系是( )A、b<a<c B、c<b<a C、c<a<b D、b<c<a10. 若某空间几何体的三视图如图所示,则该几何体的表面积是( )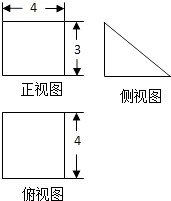 A、60 B、54 C、48 D、2411. 若幂函数f(x)=xα经过点 ,则f(x)是( )A、偶函数,且在(0,+∞)上是增函数 B、偶函数,且在(0,+∞)上是减函数 C、奇函数,且在(0,+∞)是减函数 D、非奇非偶函数,且在(0,+∞)上是增函数12. 已知直线l⊥平面α,直线m⊂平面β,给出下列命题
A、60 B、54 C、48 D、2411. 若幂函数f(x)=xα经过点 ,则f(x)是( )A、偶函数,且在(0,+∞)上是增函数 B、偶函数,且在(0,+∞)上是减函数 C、奇函数,且在(0,+∞)是减函数 D、非奇非偶函数,且在(0,+∞)上是增函数12. 已知直线l⊥平面α,直线m⊂平面β,给出下列命题①α∥β=l⊥m;
②α⊥β⇒l∥m;
③l∥m⇒α⊥β;
④l⊥m⇒α∥β.
其中正确命题的序号是( )
A、①②③ B、②③④ C、①③ D、②④二、填空题
-
13. 已知函数 ,其定义域是 .14. 圆x2+y2=2的圆心到直线 的距离为 .15. 函数y=αx﹣2﹣1(α>0且α≠1)的图象恒过的点的坐标是 .16. 圆柱形容器内盛有高度为6cm的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是cm.
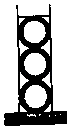
三、解答题
-
17. 已知函数f(x)= .
 (1)、在直角坐标系中画出该函数图象的草图;(2)、根据函数图象的草图,求函数y=f(x)值域,单调区间及零点.18. 已知直线l1的方程为3x+4y﹣12=0.(1)、若直线l2与l1平行,且过点(﹣1,3),求直线l2的方程;(2)、若直线l2与l1垂直,且l2与两坐标轴围成的三角形面积为4,求直线l2的方程.19. 综合:(1)、设f(x)= ,g(x)= ,证明:f(2x)=2f(x)•g(x);(2)、若xlog34=1,求4x+4﹣x的值.20. 如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.求证:
(1)、在直角坐标系中画出该函数图象的草图;(2)、根据函数图象的草图,求函数y=f(x)值域,单调区间及零点.18. 已知直线l1的方程为3x+4y﹣12=0.(1)、若直线l2与l1平行,且过点(﹣1,3),求直线l2的方程;(2)、若直线l2与l1垂直,且l2与两坐标轴围成的三角形面积为4,求直线l2的方程.19. 综合:(1)、设f(x)= ,g(x)= ,证明:f(2x)=2f(x)•g(x);(2)、若xlog34=1,求4x+4﹣x的值.20. 如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.求证: (1)、PA∥平面BDE;(2)、BD⊥平面PAC.21. 如图,四边形ABCD为矩形,四边形ADEF为梯形,AD∥FE,∠AFE=60°,∠AED=90°,且平面ABCD⊥平面ADEF,AF=FE=AB= AD=2,点G为AC的中点.
(1)、PA∥平面BDE;(2)、BD⊥平面PAC.21. 如图,四边形ABCD为矩形,四边形ADEF为梯形,AD∥FE,∠AFE=60°,∠AED=90°,且平面ABCD⊥平面ADEF,AF=FE=AB= AD=2,点G为AC的中点.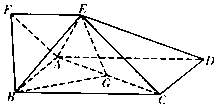
(Ⅰ)求证:平面BAE⊥平面DCE;
(Ⅱ)求三棱锥B﹣AEG的体积.
22. 已知点G(5,4),圆C1:(x﹣1)2+(y﹣4)2=25,过点G的动直线l与圆C1 , 相交于两点E、F,线段EF的中点为C.(Ⅰ)求点C的轨迹C2的方程;
(Ⅱ)若过点A(1,0)的直线l1:kx﹣y﹣k=0,与C2相交于两点P、Q,线段PQ的中点为M,l1与l2:x+2y+2=0的交点为N,求证:|AM|•|AN|为定值.