山东省威海市2016-2017学年高一上学期数学期末考试试卷

试卷日期：2017-09-16 考试类型：期末考试

前去【出卷网】下载

一、选择题

1. 下列选项中，表示同一集合的是（）

A、A={0，1}，B={（0，1）} B、A={2，3}，B={3，2} C、A={x|﹣1＜x≤1，x∈N}，B={1} D、 $A = \emptyset ， B = {x | x^{\frac{1}{2}} \leq 0}$

查看试题解析
2. 下列选项中与函数y=x是同一函数的是（）

A、 $y = \sqrt[3]{x^{3}}$ B、 $y = {(\sqrt{x})}^{2}$ C、 $y = \sqrt{x^{2}}$ D、 $y = \frac{x^{2}}{x}$

查看试题解析
3. 直线ax+2y﹣1=0与直线2x﹣3y﹣1=0垂直，则a的值为（）

A、3 B、﹣3 C、 $\frac{4}{3}$ D、 $- \frac{4}{3}$

查看试题解析
4. 如图，O为正方体ABCD﹣A₁B₁C₁D₁底面ABCD的中心，则下列直线中与D₁O垂直的是（）

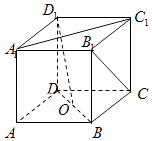A、B₁C B、AA₁ C、AD D、A₁C₁

查看试题解析
5. 下列函数在区间[0，1]上单调递增的是（）

A、y=|lnx| B、y=﹣lnx C、y=2^﹣x D、y=2^|x|

查看试题解析
6. 已知 $a = 2^{\frac{1}{2}} ， b = {(\frac{1}{2})}^{2} ， c = l o g_{2} \frac{1}{2}$ ，则三个数的大小关系正确的是（）

A、b＜a＜c B、c＜a＜b C、c＜b＜a D、b＜c＜a

查看试题解析
7. 设l、m两条不同的直线，α是一个平面，则下列命题不正确的是（）

A、若l⊥α，m⊂α，则l⊥m B、若l⊥α，l∥m，则m⊥α C、若l⊥α，则m⊥α，则l∥m D、若l∥α，m∥α，则l∥m

查看试题解析
8. 两平行直线x+2y﹣1=0与2x+4y+3=0间的距离为（）

A、 $\frac{2}{5} \sqrt{5}$ B、 $\frac{\sqrt{5}}{2}$ C、 $\frac{4}{5} \sqrt{5}$ D、 $\sqrt{5}$

查看试题解析
9. 已知函数g（x）=a^x﹣f（x）（a＞0且a≠1），其中f（x）是定义在[a﹣6，2a]上的奇函数，若 $g (- 1) = \frac{5}{2}$ ，则g（1）=（）

A、0 B、﹣3 C、1 D、﹣1

查看试题解析
10. 一笔投资的回报方案为：第一天回报0.5元，以后每天的回报翻一番，则投资第x天与当天的投资回报y之间的函数关系为（）

A、y=0.5x² ， x∈N^* B、y=2^x ， x∈N^* C、y=2^x^﹣1 ， x∈N^* D、y=2^x^﹣2 ， x∈N^*

查看试题解析
11. 将棱长为2的正方体（图1）切割后得一几何体，其三视图如图2所示，则该几何体的体积为（）

A、 $\frac{4}{3}$ B、 $\frac{8}{3}$ C、2 D、4

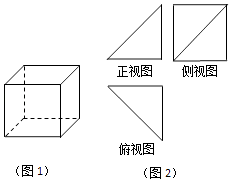查看试题解析
12. 已知函数f（x）=a（x+a）（x﹣a+3），g（x）=2^x+2﹣1，若对任意x∈R，f（x）＞0和g（x）＞0至少有一个成立，则实数a的取值范围是（）

A、（1，2） B、（2，3） C、（﹣2，﹣1）∪（1，+∞） D、（0，2）

查看试题解析

二、填空题

13. 一圆锥的母线长为20，母线与轴的夹角为30°，则圆锥的表面积为．

查看试题解析
14. 计算 ${(\frac{8}{27})}^{- \frac{2}{3}} + l g 25 + l g 4 + 3^{l o g_{3} 2}$ = ．

查看试题解析
15. 已知函数 $f (x) = {\begin{matrix} 3 x - \frac{1}{2} ， x < 1 \\ 2^{x} ， x \geq 1. \end{matrix}$ 则 $f (f (\frac{1}{2}))$ = ．

查看试题解析
16. 下列四个结论：
①函数 $y = {0.7}^{\frac{1}{x}}$ 的值域是（0，+∞）；
②直线2x+ay﹣1=0与直线（a﹣1）x﹣ay﹣1=0平行，则a=﹣1；
③过点A（1，2）且在坐标轴上的截距相等的直线的方程为x+y=3；
④若圆柱的底面直径与高都等于球的直径，则圆柱的侧面积等于球的表面积．
其中正确的结论序号为．

查看试题解析

三、解答题

17. 已知平面内点A（1，3），B（﹣2，﹣1），C（4，m）．
（Ⅰ）若A，B，C三点共线，求实数m的值；
（Ⅱ）若△ABC的面积为6，求实数m的值．

查看试题解析
18. 已知函数 $f (x) = \sqrt{5 - x} + l g (x + 1)$ 的定义域为集合A，函数g（x）=lg（x²﹣2x+a）的定义域为集合B．
（Ⅰ）当a=﹣8时，求A∩B；
（Ⅱ）若A∩∁_RB={x|﹣1＜x≤3}，求a的值．

查看试题解析
19. 已知四棱锥P﹣ABCD，底面ABCD为正方形，侧面PAD为直角三角形，且PA=PD，面PAD⊥面ABCD，E、F分别为AB、PD的中点．
（Ⅰ）求证：EF∥面PBC；
（Ⅱ）求证：AP⊥面PCD．

查看试题解析
20. 光线l₁从点M（﹣1，3）射到x轴上，在点P（1，0）处被x轴反射，得到光线l₂ ，再经直线x+y﹣4=0反射，得到光线l₃ ，求l₂和l₃的方程．

查看试题解析
21. 函数f（x）=（k﹣2）x²+2kx﹣3．
（Ⅰ）当k=4时，求f（x）在区间（﹣4，1）上的值域；
（Ⅱ）若函数f（x）在（0，+∞）上至少有一个零点，求实数k的取值范围；
（Ⅲ）若f（x）在区间[1，2]上单调递增，求实数k的取值范围．

查看试题解析
22. 函数f（x）的图象如图所示，曲线BCD为抛物线的一部分．
（Ⅰ）求f（x）解析式；
（Ⅱ）若f（x）=1，求x的值；
（Ⅲ）若f（x）＞f（2﹣x），求x的取值范围．

查看试题解析