江西省上饶市2016-2017学年高一上学期数学期末考试试卷

试卷日期：2017-09-16 考试类型：期末考试

前去【出卷网】下载

一、选择题

1. 已知直线ax+2y+2=0与3x﹣y﹣2=0平行，则系数a=（）

A、3 B、﹣6 C、﹣ $\frac{3}{2}$ D、 $\frac{2}{3}$

查看试题解析
2. 函数f（x）=ln（x²﹣x）的定义域为（　　）

A、（0，1） B、[0，1] C、（﹣∞，0）∪（1，+∞） D、（﹣∞，0]∪[1，+∞）

查看试题解析
3. 若l，m是两条不同的直线，α是一个平面，则下列命题正确的是（）

A、若l∥α，m∥α，则l∥m B、若l⊥m，m⊂α，则l⊥α C、若l∥α，m⊂α，则l∥m D、若l⊥α，l∥m，则m⊥α

查看试题解析
4. 已知点（3，m）到直线x+y﹣4=0的距离等于 $\sqrt{2}$ ，则m=（）

A、3 B、2 C、3或﹣1 D、2或﹣1

查看试题解析
5. 若x∈（e^﹣¹ ， 1），a=lnx，b=（ $\frac{1}{2}$ ）^lnx ， c=e^lnx ，则a，b，c的大小关系为（）

A、c＞b＞a B、b＞c＞a C、a＞b＞c D、b＞a＞c

查看试题解析
6. 函数f（x）=ln x﹣ $\frac{1}{x - 1}$ 的零点的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 函数y=（ $\frac{1}{2}$ ） $^{2 x^{2} - 3 x + 1}$ 的递减区间为（）

A、[ $\frac{3}{4}$ ，+∞） B、（﹣∞， $\frac{3}{4}$ ] C、（﹣∞，1） D、（1，+∞）

查看试题解析
8. 已知函数y=log₂（ax﹣1）在（﹣2，﹣1）上单调递减，则实数a的取值范围是（）

A、（﹣1，0] B、[﹣2，﹣1] C、（﹣∞，﹣1] D、（﹣∞，﹣1）

查看试题解析
9. 长方体的一个顶点上三条棱长分别为3、4、5，且它的8个顶点都在同一球面上，则这个球的表面积是（）

A、25π B、50π C、125π D、75π

查看试题解析
10. 一空间几何体的三视图如图所示，则该几何体的体积为（）

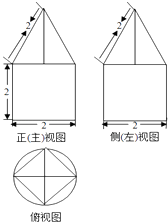A、2π+2 $\sqrt{3}$ B、4π+2 $\sqrt{3}$ C、2π+ $\frac{2 \sqrt{3}}{3}$ D、4π+ $\frac{2 \sqrt{3}}{3}$

查看试题解析
11. 已知函数f（x）=x⁵+ax³+bx﹣8，且f（﹣2017）=10，则f（2017）等于（）

A、﹣26 B、﹣18 C、﹣10 D、10

查看试题解析
12. 已知函数 $f (x) = {\begin{matrix} a x^{2} + 2 x + 1 ， (x \leq 0) \\ a x - 3 ， (x > 0) \end{matrix}$ 有3个零点，则实数a的取值范围是（）

A、a＜1 B、a＞0 C、a≥1 D、0＜a＜1

查看试题解析

二、填空题

13. 已知集合A={x|x∈N， $\frac{12}{6 - x}$ ∈N}，则集合A用列举法表示为

查看试题解析
14. 函数 $f (x) = (m^{2} - m - 1) x^{m^{2} - 2 m - 3}$ 是幂函数，且在x∈（0，+∞）上是减函数，则实数m= ．

查看试题解析
15. 过点P（2，﹣1），在x轴上和y轴上的截距分别是a，b且满足a=3b的直线方程为．

查看试题解析
16. 若[x]表示不超过x的最大整数，则[lg2]+[lg3]+…+lg[2017]+[lg $\frac{1}{2}$ ]+[lg $\frac{1}{3}$ ]+…+[lg $\frac{1}{2017}$ ]= ．

查看试题解析

三、解答题

17. 已知全集为全体实数R，集合A={x|3≤x≤7}，B={x|2＜x＜10}，C={x|x＜a}．

(1)、求（∁_RA）∩B；

(2)、若A∩C≠∅，求a的取值范围．

查看试题解析
18. 计算：

(1)、求值：（0.064） $^{- \frac{1}{3}}$ ﹣（﹣ $\frac{1}{2 \sqrt{2}}$ ）^﹣2÷16^0.75+（ $\sqrt{2}$ ﹣2017）⁰；

(2)、求值： $\frac{l g \sqrt{27} + l g 8 - l g \sqrt{1000}}{l g 1.2}$ ．

查看试题解析
19. 如图，三棱锥V﹣ABC中，VA=VB=AC=BC=2，AB= $2 \sqrt{3}$ ，VC=1．
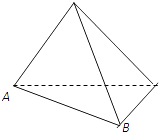
（Ⅰ）证明：AB⊥VC；
（Ⅱ）求三棱锥V﹣ABC的体积．

查看试题解析
20. 已知△ABC的顶点A（1，3），AB边上的中线CM所在直线方程为2x﹣3y+2=0，AC边上的高BH所在直线方程为2x+3y﹣9=0．求：

(1)、顶点C的坐标；

(2)、直线BC的方程．

查看试题解析
21. 如图所示，在等腰梯形CDEF中，DE=CD= $\sqrt{2}$ ，EF=2+ $\sqrt{2}$ ，将它沿着两条高AD，CB折叠成如图（2）所示的四棱锥E﹣ABCD（E，F重合）．

(1)、求证：BE⊥DE；

(2)、设点M为线段AB的中点，试在线段CE上确定一点N，使得MN∥平面DAE．

查看试题解析
22. 已知指数函数y=g（x）满足：g（3）=8，定义域为R的函数f（x）= $\frac{n - g (x)}{m + 2 g (x)}$ 是奇函数．

(1)、确定y=g（x），y=f（x）的解析式；

(2)、若h（x）=f（x）+a在（﹣1，1）上有零点，求a的取值范围；

(3)、若对任意的t∈（﹣4，4），不等式f（6t﹣3）+f（t²﹣k）＜0恒成立，求实数k的取值范围．

查看试题解析