河南省焦作市2016-2017学年高一上学期数学期末考试试卷
试卷日期:2017-09-16 考试类型:期末考试
一、选择题
-
1. 已知集合A={x|ax2﹣5x+6=0},若2∈A,则集合A的子集个数为( )A、4 B、3 C、2 D、12. 一个圆锥的侧面展开图是一个半径为2的半圆,则该圆锥的体积为( )A、2 π B、 π C、 D、3. 已知集合A={x∈N*|﹣2<x≤2},B={y|y=2x , x∈A}|,C={z|z=1+log2y,y∈B},则A∩C=( )A、{1,2} B、{2} C、{2,3,4} D、{1,2,3,4}4. 函数f(x)=( )x+ ﹣3的零点所在区间是( )A、(1,2) B、(0,1) C、(﹣1,0) D、(﹣2,﹣1)5. 如图为一个几何体的三视图,三视图中的两个不同的正方形的边长分别为1和2,则该几何体的体积为( )
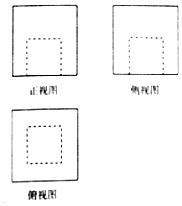 A、6 B、7 C、8 D、96. 已知α、β是两个不同平面,m,n,l是三条不同直线,则下列命题正确的是( )A、若m∥α,n⊥β且m⊥n,则α⊥β B、若m⊂α,n⊂α,l⊥n,则l⊥α C、若m∥α,n⊥β且α⊥β,则m∥n D、若l⊥α且l⊥β,则α∥β7. 已知幂函数f(x)=xk的图象经过函数g(x)=ax﹣2﹣ (a>0且a≠1)的图象所过的定点,则f( )的值等于( )A、8 B、4 C、2 D、18. 已知直线l1:x+2y+t2=0和直线l2:2x+4y+2t﹣3=0,则当l1与l2间的距离最短时t的值为( )A、1 B、 C、 D、29. 函数y=e|x|﹣x3的大致图象是( )A、
A、6 B、7 C、8 D、96. 已知α、β是两个不同平面,m,n,l是三条不同直线,则下列命题正确的是( )A、若m∥α,n⊥β且m⊥n,则α⊥β B、若m⊂α,n⊂α,l⊥n,则l⊥α C、若m∥α,n⊥β且α⊥β,则m∥n D、若l⊥α且l⊥β,则α∥β7. 已知幂函数f(x)=xk的图象经过函数g(x)=ax﹣2﹣ (a>0且a≠1)的图象所过的定点,则f( )的值等于( )A、8 B、4 C、2 D、18. 已知直线l1:x+2y+t2=0和直线l2:2x+4y+2t﹣3=0,则当l1与l2间的距离最短时t的值为( )A、1 B、 C、 D、29. 函数y=e|x|﹣x3的大致图象是( )A、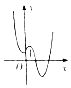 B、
B、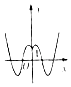 C、
C、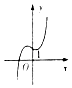 D、
D、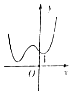 10. 如图,在底面为正方形的四棱锥P﹣ABCD中,侧面PAD⊥底面ABCD,PA⊥AD,PA=AD,则异面直线PB与AC所成的角为( )
10. 如图,在底面为正方形的四棱锥P﹣ABCD中,侧面PAD⊥底面ABCD,PA⊥AD,PA=AD,则异面直线PB与AC所成的角为( )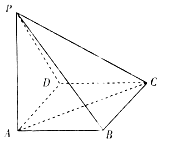 A、30° B、45° C、60° D、90°11. 若圆C1:(x﹣1)2+(y+3)2=1与圆C2:(x﹣a)2+(y﹣b)2=1外离,过直线l:x﹣y﹣1=0上任意一点P分别做圆C1 , C2的切线,切点分别为M,N,且均保持|PM|=|PN|,则a+b=( )A、﹣2 B、﹣1 C、1 D、212. 已知y=f(x)是定义在R上的奇函数,且当x<0时f(x)= 则方程f(x﹣2)=﹣ (x﹣2)的实数根的个数为( )A、8 B、7 C、6 D、5
A、30° B、45° C、60° D、90°11. 若圆C1:(x﹣1)2+(y+3)2=1与圆C2:(x﹣a)2+(y﹣b)2=1外离,过直线l:x﹣y﹣1=0上任意一点P分别做圆C1 , C2的切线,切点分别为M,N,且均保持|PM|=|PN|,则a+b=( )A、﹣2 B、﹣1 C、1 D、212. 已知y=f(x)是定义在R上的奇函数,且当x<0时f(x)= 则方程f(x﹣2)=﹣ (x﹣2)的实数根的个数为( )A、8 B、7 C、6 D、5二、填空题
-
13. 设函数f(x)= ,则f(f( ))= .14. 圆O1:(x﹣2)2+(y+3)2=4与圆O2:(x+1)2+(y﹣1)2=9的公切线有条.15. 如图所示,已知G,G1分别是棱长为4的正方体ABCD﹣A1B1C1D1的下底面和上地面的中心,点P在线段GG1上运动,点Q在下底面ABCD内运动,且始终保持PQ=2,则线段PQ的中点M运动形成的曲面与正方体下底面所围成的几何体的体积为 .
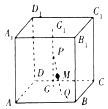 16. 函数f(x)=(2x﹣2)2+(2﹣x+2)2﹣10在区间[1,2]上的最大值与最小值之积为 .
16. 函数f(x)=(2x﹣2)2+(2﹣x+2)2﹣10在区间[1,2]上的最大值与最小值之积为 .三、解答题
-
17. 已知集合A={x|y= },B={x|x<﹣4或x>2}(1)、若m=﹣2,求A∩(∁RB);(2)、若A∪B=B,求实数m的取值范围.18. 在平面直角坐标系xOy中,已知△ABC的顶点A(5,1),B(1,5).(1)、若A为直角△ABC的直角顶点,且顶点C在y轴上,求BC边所在直线方程;(2)、若等腰△ABC的底边为BC,且C为直线l:y=2x+3上一点,求点C的坐标.19. 已知函数f(x)=logax(a>0且a≠1)在区间[1,2]上的最大值与函数g(x)=﹣ 在区间[1,2]上的最大值互为相反数.(1)、求a的值;(2)、若函数F(x)=f(x2﹣mx﹣m)在区间(﹣∞,1﹣ )上是减函数,求实数m的取值范围.20. 已知半径为 ,圆心在直线l1:x﹣y+1=0上的圆C与直线l2: x﹣y+1﹣ =0相交于M,N两点,且|MN|=(1)、求圆C的标准方程;(2)、当圆心C的横、纵坐标均为整数时,若对任意m∈R,直线l3:mx﹣y+ +1=0与圆C恒有公共点,求实数a的取值范围.21. 如图,在直三棱柱ABC﹣A1B1C1中,P,Q分别是AA1 , B1C1上的点,且AP=3A1P,B1C1=4B1Q.
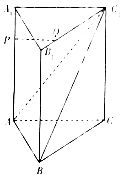 (1)、求证:PQ∥平面ABC1;(2)、若AB=AA1 , BC=3,AC1=3,BC1= ,求证:平面ABC1⊥平面AA1C1C.22. 已知函数f(x)对任意实数x,y均有f(x)=f( )+f( ).当x>0时,f(x)>0(1)、判断函数f(x)在R上的单调性并证明;(2)、设函数g(x)与函数f(x)的奇偶性相同,当x≥0时,g(x)=|x﹣m|﹣m(m>0),若对任意x∈R,不等式g(x﹣1)≤g(x)恒成立,求实数m的取值范围.
(1)、求证:PQ∥平面ABC1;(2)、若AB=AA1 , BC=3,AC1=3,BC1= ,求证:平面ABC1⊥平面AA1C1C.22. 已知函数f(x)对任意实数x,y均有f(x)=f( )+f( ).当x>0时,f(x)>0(1)、判断函数f(x)在R上的单调性并证明;(2)、设函数g(x)与函数f(x)的奇偶性相同,当x≥0时,g(x)=|x﹣m|﹣m(m>0),若对任意x∈R,不等式g(x﹣1)≤g(x)恒成立,求实数m的取值范围.