安徽省蚌埠市2016-2017学年高考理数三模考试试卷

试卷日期：2017-09-11 考试类型：高考模拟

前去【出卷网】下载

一、选择题

1. 设全集U={x|e^x＞1}，函数f（x）= $\frac{1}{\sqrt{x - 1}}$ 的定义域为A，则∁_UA为（）

A、（0，1] B、（0，1） C、（1，+∞） D、[1，+∞）

查看试题解析
2. 复数z的共轭复数为 $\bar{z}$ ，若 $\frac{1 - i}{z \cdot \bar{z} + i}$ 为纯虚数，则|z|=（）

A、2 B、 $\sqrt{3}$ C、 $\sqrt{2}$ D、1

查看试题解析
3. 已知向量 $\vec{a}$ 、 $\vec{b}$ 夹角为60°，且| $\vec{a}$ |=2，| $\vec{a}$ ﹣2 $\vec{b}$ |=2 $\sqrt{7}$ ，则| $\vec{b}$ |=（）

A、2 B、﹣2 C、3 D、﹣3

查看试题解析
4. 已知公差不为0的等差数列{a_n}满足a₁ ， a₃ ， a₄成等比数列，S_n为数列{a_n}的前n项和，则 $\frac{S_{3} - S_{2}}{S_{5} - S_{3}}$ 的值为（）

A、2 B、3 C、﹣2 D、﹣3

查看试题解析
5. 在如图所示的正方形中随机选择10000个点，则选点落入阴影部分（边界曲线C为正态分布N（﹣1，1）的密度曲线的一部分）的点的个数的估计值为（）
附：若X：N（μ，δ²），则P（μ﹣δ＜X≤μ+δ）=0.6826．P（μ﹣δ＜X≤μ+2δ）=0.9544．

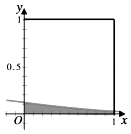A、906 B、1359 C、2718 D、3413

查看试题解析
6. 如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体各面直角三角形的个数是（）

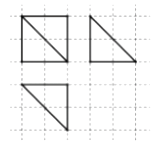A、2 B、3 C、4 D、5

查看试题解析
7. 二分法是求方程近似解的一种方法，其原理是“一分为二、无限逼近”．执行如图所示的程序框图，若输入x₁=1，x₂=2，d=0.01则输出n的值（）

A、6 B、7 C、8 D、9

查看试题解析
8. 设x，y满足约束条件 ${\begin{matrix} x \geq 0 \\ y \geq 0 \\ 2 x + y \leq 2 \end{matrix}$ ，目标函数z=ax+by（a＞0，b＞0）的最大值为M，若M的取值范围是[1，2]，则点M（a，b）所经过的区域面积为（）

A、 $\frac{1}{2}$ B、 $\frac{3}{2}$ C、 $\frac{5}{2}$ D、 $\frac{7}{2}$

查看试题解析
9. 已知函数f（x）=2sin（ωx+φ）+1（ω＞0，|φ|≤ $\frac{π}{2}$ ），其图象与直线y=﹣1相邻两个交点的距离为π，若f（x）＞1对∀x∈（﹣ $\frac{π}{12}$ ， $\frac{π}{3}$ ）恒成立，则φ的取值范围是（）

A、 $[\frac{π}{12} ， \frac{π}{6}]$ B、 $[\frac{π}{6} ， \frac{π}{2}]$ C、 $[\frac{π}{12} ， \frac{π}{3}]$ D、 $[\frac{π}{6} ， \frac{π}{3}]$

查看试题解析
10. 已知椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}}$ =1（a＞b＞0）的左、右焦点分别为F₁ ， F₂ ，过F₂作一条直线（不与x轴垂直）与椭圆交于A，B两点，如果△ABF₁恰好为等腰直角三角形，该直线的斜率为（）

A、±1 B、±2 C、 $\pm \sqrt{2}$ D、 $\pm \sqrt{3}$

查看试题解析
11. 现有10支队伍参加篮球比赛，规定：比赛采取单循环比赛制，即每支队伍与其他9支队伍各比赛一场；每场比赛中，胜方得2分，负方得0分，平局双方各得1分．下面关于这10支队伍得分的叙述正确的是（）

A、可能有两支队伍得分都是18分 B、各支队伍得分总和为180分 C、各支队伍中最高得分不少于10分 D、得偶数分的队伍必有偶数个

查看试题解析
12. 已知AD与BC是四面体ABCD中相互垂直的棱，若AD=BC=6，且∠ABD=∠ACD=60°，则四面体ABCD的体积的最大值是（）

A、 $18 \sqrt{2}$ B、 $36 \sqrt{2}$ C、18 D、36

查看试题解析

二、填空题

13. ${(2 x - \frac{1}{\sqrt{x}})}^{5}$ 的展开式中， $\sqrt{x}$ 的系数为．

查看试题解析
14. 已知函数f（x）=ax³+bx+1，若f（a）=8，则f（﹣a）= ．

查看试题解析
15. 已知双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a ， b > 0)$ ，过x轴上点P的直线与双曲线的右支交于M，N两点（M在第一象限），直线MO交双曲线左支于点Q（O为坐标原点），连接QN．若∠MPO=60°，∠MNQ=30°，则该双曲线的离心率为．

查看试题解析
16. 已知数列{a_n}满足a₁= $\frac{1}{256} ， a_{n + 1} = 2 \sqrt{a_{n}}$ ，若b_n=log₂a_n﹣2，则b₁•b₂•…•b_n的最大值为．

查看试题解析

三、解答题

17. 已知△ABC的内角A，B，C的对边分别为a，b，c，且ctanC= $\sqrt{3}$ （acosB+bcosA）．

(1)、求角C；

(2)、若c=2 $\sqrt{3}$ ，求△ABC面积的最大值．

查看试题解析
18. 当今信息时代，众多中小学生也配上了手机．某机构为研究经常使用手机是否对学习成绩有影响，在某校高三年级50名理科生第人的10次数学考成绩中随机抽取一次成绩，用茎叶图表示如图：

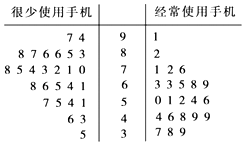(1)、根据茎叶图中的数据完成下面的2×2列联表，并判断是否有95%的把握认为经常使用手机对学习成绩有影响？
及格（60及60以上）
不及格
合计
很少使用手机
经常使用手机
合计

(2)、从50人中，选取一名很少使用手机的同学（记为甲）和一名经常使用手机的同学（记为乙）解一道函数题，甲、乙独立解决此题的概率分别为P₁ ， P₂ ， P₂=0.4，若P₁﹣P₂≥0.3，则此二人适合为学习上互帮互助的“对子”，记X为两人中解决此题的人数，若E（X）=1.12，问两人是否适合结为“对子”？
参考公式及数据： $K^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ，其中n=a+b+c+d
P（K²≥k₀）
0.10
0.05
0.025
k₀
2.706
3.841
5.024

查看试题解析
19. 如图所示，四面体ABCD中，已知平面BCD⊥平面ABC，BD⊥DC，BC=6，AB=4 $\sqrt{3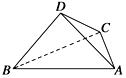}$ ，∠ABC=30°．

(1)、求证：AC⊥BD；

(2)、若二面角B﹣AC﹣D为45°，求直线AB与平面ACD所成的角的正弦值．

查看试题解析
20. 已知过抛物线E：x²=2py（p＞0）焦点F且倾斜角的60°直线l与抛物线E交于点M，N，△OMN的面积为4．

(1)、求抛物线E的方程；

(2)、设P是直线y=﹣2上的一个动点，过P作抛物线E的切线，切点分别为A、B，直线AB与直线OP、y轴的交点分别为Q、R，点C、D是以R为圆心、RQ为半径的圆上任意两点，求∠CPD最大时点P的坐标．

查看试题解析
21. 已知f（x）=ln（ax+b）+x²（a≠0）．

(1)、若曲线y=f（x）在点（1，f（1））处的切线方程为y=x，求a，b的值；

(2)、若f（x）≤x²+x恒成立，求ab的最大值．

查看试题解析
22. 在平面直角坐标系xOy中，直线l的参数方程为 ${\begin{matrix} x = 1 + t c o s α \\ y = 1 + t s i n α \end{matrix}$ （t为参数，0≤α＜π），以坐标原点O为极点，x轴的正半轴为极轴，并取相同的长度单位，建立极坐标系．曲线C₁：p=1．

(1)、若直线l与曲线C₁相交于点A，B，点M（1，1），证明：|MA|•|MB|为定值；

(2)、将曲线C₁上的任意点（x，y）作伸缩变换 ${\begin{matrix} x' = \sqrt{3 x} \\ y' = y \end{matrix}$ 后，得到曲线C₂上的点（x'，y'），求曲线C₂的内接矩形ABCD周长的最大值．

查看试题解析
23. 已知a＞0，b＞0，函数f（x）=|x+a|+|2x﹣b|的最小值为1．

(1)、求证：2a+b=2；

(2)、若a+2b≥tab恒成立，求实数t的最大值．

查看试题解析

	及格（60及60以上）	不及格	合计
很少使用手机
经常使用手机
合计

P（K²≥k₀）	0.10	0.05	0.025
k₀	2.706	3.841	5.024