四川省绵阳市2016-2017学年高一上学期数学期末考试试卷
试卷日期:2017-08-31 考试类型:期末考试
一、选择题
-
1. 如果全集U={1,2,3,4,5},M={1,2,5},则∁UM=( )A、{1,2} B、{3,4} C、{5} D、{1,2,5}2. 函数f(x)= 的定义域是( )A、(﹣∞, ) B、(﹣∞,0] C、(0,+∞) D、(﹣∞,0)3. 一个半径是R的扇形,其周长为4R,则该扇形圆心角的弧度数为( )A、1 B、2 C、π D、4. 下列各组中的函数f(x),g(x)表示同一函数的是( )A、f(x)=x,g(x)= B、f(x)=x+1,g(x)= C、f(x)=|x|,g(x)= D、f(x)=log22x , g(x)=2log2x5. 设函数f(x)= ,则f(f(2))=( )A、 B、16 C、 D、46. 已知幂函数y=f(x)的图象过点(2, ),则下列说法正确的是( )A、f(x)是奇函数,则在(0,+∞)上是增函数 B、f(x)是偶函数,则在(0,+∞)上是减函数 C、f(x)既不是奇函数也不是偶函数,且在(0,+∞)上是增函数 D、f(x)既不是奇函数也不是偶函数,且在(0,+∞)上是减函数7. 若函数f(x)=x2﹣a|x|+a2﹣3有且只有一个零点,则实数a=( )A、 B、﹣ C、2 D、08. 把函数f(x)=sin2x的图象向左平移 个单位,所得图象的解析式是( )A、y=sin(2x+ ) B、y=sin(2x﹣ ) C、y=cos2x D、y=﹣cos2x9. 函数f(x)= 的大致图象是( )A、
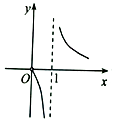 B、
B、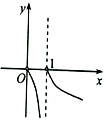 C、
C、 D、
D、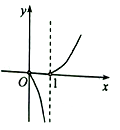 10. 设f(x)是R上的偶函数,且在[0,+∞)上是单调递增,若f(2)=0,则使f(log x)<0成立的x的取值范围是( )A、( ,4) B、(0, ) C、( , ) D、( ,4)11. 记[x]表示不超过x的最大整数,如[1.2]=1,[0.5]=0,则方程[x]﹣x=lnx的实数根的个数为( )A、0 B、1 C、2 D、312. 已知函数y=sinx+1与y= 在[﹣a,a](a∈Z,且a>2017)上有m个交点(x1 , y1),(x2 , y2),…,(xm , ym),则(x1+y1)+(x2+y2)+…+(xm+ym)=( )A、0 B、m C、2m D、2017
10. 设f(x)是R上的偶函数,且在[0,+∞)上是单调递增,若f(2)=0,则使f(log x)<0成立的x的取值范围是( )A、( ,4) B、(0, ) C、( , ) D、( ,4)11. 记[x]表示不超过x的最大整数,如[1.2]=1,[0.5]=0,则方程[x]﹣x=lnx的实数根的个数为( )A、0 B、1 C、2 D、312. 已知函数y=sinx+1与y= 在[﹣a,a](a∈Z,且a>2017)上有m个交点(x1 , y1),(x2 , y2),…,(xm , ym),则(x1+y1)+(x2+y2)+…+(xm+ym)=( )A、0 B、m C、2m D、2017二、填空题
-
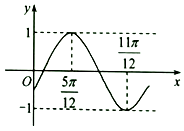
13. 计算:lg ﹣lg25= .14. 在△ABC中,已知tanA= ,则cos5A= .15. 函数f(x)=sin(ωx+φ)(ω>0,﹣ <φ< )的部分图象如图所示,则f(0)= .
 16. 雾霾是人体健康的隐形杀手,爱护环境,人人有责.某环保实验室在雾霾天采用清洁剂处理教室空气质量.实验发现,当在教室释放清洁剂的过程中,空气中清洁剂的含剂浓度y(mg/m3)与时间t(h)成正比;释放完毕后,y与t的函数关系为y=( )t﹣a(a为常数),如图,已知当教室的空气中含剂浓度在0.25mg/m3以上时,教室最适合人体活动.根据图中信息,从一次释放清洁剂开始,这间教室有 h最适合人体活动.
16. 雾霾是人体健康的隐形杀手,爱护环境,人人有责.某环保实验室在雾霾天采用清洁剂处理教室空气质量.实验发现,当在教室释放清洁剂的过程中,空气中清洁剂的含剂浓度y(mg/m3)与时间t(h)成正比;释放完毕后,y与t的函数关系为y=( )t﹣a(a为常数),如图,已知当教室的空气中含剂浓度在0.25mg/m3以上时,教室最适合人体活动.根据图中信息,从一次释放清洁剂开始,这间教室有 h最适合人体活动.
三、解答题
-
17. 已知函数f(x)= ,x∈[2,6].(1)、证明f(x)是减函数;(2)、若函数g(x)=f(x)+sinα的最大值为0,求α的值.18. 已知函数f(x)=sinx+cos(x+ ),x∈R.(1)、求f(x)的最小正周期及单调递增区间;(2)、若x是第二象限角,且f(x﹣ )=﹣ cos2x,求cosx﹣sinx的值.19. 如图,有一块半径为2的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上.设∠DAB=θ(0<θ< ),L为等腰梯形ABCD的周长.
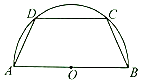 (1)、求周长L与θ的函数解析式;(2)、试问周长L是否存在最大值?若存在,请求出最大值,并指出此时θ的大小;若不存在,请说明理由.20. 已知函数f(x)=loga ,g(x)=loga(x+2a)+loga(4a﹣x),其中a>0,且a≠1.(1)、求f(x)的定义域,并判断f(x)的奇偶性;(2)、已知区间D=[2a+1,2a+ ]满足3a∉D,设函数h(x)=f(x)+g(x),h(x)的定义域为D,若对任意x∈D,不等式|h(x)|≤2恒成立,求实数a的取值范围.
(1)、求周长L与θ的函数解析式;(2)、试问周长L是否存在最大值?若存在,请求出最大值,并指出此时θ的大小;若不存在,请说明理由.20. 已知函数f(x)=loga ,g(x)=loga(x+2a)+loga(4a﹣x),其中a>0,且a≠1.(1)、求f(x)的定义域,并判断f(x)的奇偶性;(2)、已知区间D=[2a+1,2a+ ]满足3a∉D,设函数h(x)=f(x)+g(x),h(x)的定义域为D,若对任意x∈D,不等式|h(x)|≤2恒成立,求实数a的取值范围.