江苏省泰州市高港区2016-2017年中考三模数学考试试卷
试卷日期:2017-08-23 考试类型:中考模拟
一、选择题
-
1. 2的相反数是( )A、﹣2 B、﹣ C、 D、22. 等于( )A、﹣3 B、3 C、±3 D、3. 南京青奥会期间约有1020000人次参与了青奥文化教育活动.将数据1020000用科学记数法表示为( )A、10.2×105 B、1.02×105 C、1.02×106 D、1.02×1074. 如图,∠1=50°,如果AB∥DE,那么∠D=( )
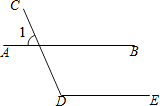 A、40° B、50° C、130° D、140°5. 刻画一组数据波动大小的统计量是( )A、平均数 B、方差 C、众数 D、中位数6. 如图,水平线l1∥l2 , 铅垂线l3∥l4 , l1⊥l3 , 若选择l1、l2其中一条当成x轴,且向右为正方向,再选择l3、l4其中一条当成y轴,且向上为正方向,并在此平面直角坐标系中画出二次函数y=ax2﹣ax﹣a的图象,则下列关于x、y轴的叙述,正确的是( )
A、40° B、50° C、130° D、140°5. 刻画一组数据波动大小的统计量是( )A、平均数 B、方差 C、众数 D、中位数6. 如图,水平线l1∥l2 , 铅垂线l3∥l4 , l1⊥l3 , 若选择l1、l2其中一条当成x轴,且向右为正方向,再选择l3、l4其中一条当成y轴,且向上为正方向,并在此平面直角坐标系中画出二次函数y=ax2﹣ax﹣a的图象,则下列关于x、y轴的叙述,正确的是( )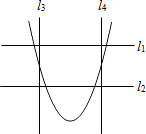 A、l1为x轴,l3为y轴 B、l1为x轴,l4为y轴 C、l2为x轴,l3为y轴 D、l2为x轴,l4为y轴
A、l1为x轴,l3为y轴 B、l1为x轴,l4为y轴 C、l2为x轴,l3为y轴 D、l2为x轴,l4为y轴二、填空题
-
7. 使式子 有意义的x取值范围是 .8. 一组数据1,4,2,5,3的中位数是 .9. 在比例尺为1:200000的地图上,小明家到单位的图上距离为20cm,则小明家到单位的实际距离为千米.10. 若圆锥的底面半径为2cm,母线长为5cm,则此圆锥的表面积为 .11. 已知△ABC的周长为24,面积为48,则它的内切圆的半径为 .12. 若m<﹣2,则下列函数:①y= (x>0);②y=﹣mx+1;③y=mx;④y=(m+1)x﹣1中y随x的增大而增大的函数是 . (填序号)13. 如图,△ABC内接于⊙O,∠B=30°,AC=2cm,则⊙O半径长为 cm.
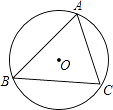 14. 如图,在矩形ABCD中,点E为边CD上一点,沿AE折叠,点D恰好落在BC边上的F点处,若AB=3,BC=5,则tan∠EFC的值为 .
14. 如图,在矩形ABCD中,点E为边CD上一点,沿AE折叠,点D恰好落在BC边上的F点处,若AB=3,BC=5,则tan∠EFC的值为 .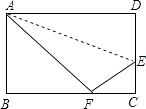 15. 如图,已知双曲线y= (k>0)经过直角三角形OAB斜边OB的中点D,与直角边AB相交于点C.若△OBC的面积为3,则k= .
15. 如图,已知双曲线y= (k>0)经过直角三角形OAB斜边OB的中点D,与直角边AB相交于点C.若△OBC的面积为3,则k= .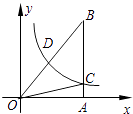 16. 如图,矩形ABCD中,AB=4,BC=3,边CD在直线l上,将矩形ABCD沿直线l作无滑动翻滚,当点A第一次翻滚到点A1位置时,则点A经过的路线长为 .
16. 如图,矩形ABCD中,AB=4,BC=3,边CD在直线l上,将矩形ABCD沿直线l作无滑动翻滚,当点A第一次翻滚到点A1位置时,则点A经过的路线长为 .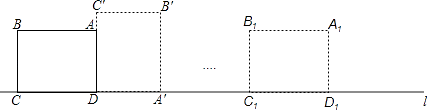
三、解答题
-
17. 根据要求进行计算:(1)、计算:( )﹣2﹣(π﹣2011)0+| ﹣2|+2cos45°.(2)、先化简,再求值:( + )÷ ,其中x= ﹣1.18. 为增强学生体质,各学校普遍开展了阳光体育活动,某校为了解全校1000名学生每周课外体育活动时间的情况,随机调查了其中的50名学生,对这50名学生每周课外体育活动时间x(单位:小时)进行了统计.根据所得数据绘制了一幅不完整的统计图,并知道每周课外体育活动时间在6≤x<8小时的学生人数占24%.根据以上信息及统计图解答下列问题:
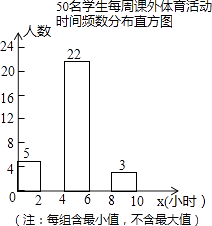 (1)、本次调查属于调查,样本容量是;(2)、请补全频数分布直方图中空缺的部分;(3)、求这50名学生每周课外体育活动时间的平均数;(4)、估计全校学生每周课外体育活动时间不少于6小时的人数.19. 在▱ABCD中,AB=2BC=4,E、F分别为AB、CD的中点
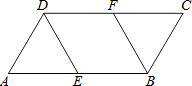
(1)、本次调查属于调查,样本容量是;(2)、请补全频数分布直方图中空缺的部分;(3)、求这50名学生每周课外体育活动时间的平均数;(4)、估计全校学生每周课外体育活动时间不少于6小时的人数.19. 在▱ABCD中,AB=2BC=4,E、F分别为AB、CD的中点①求证:△ADE≌△CBF;
②若四边形DEBF为菱形,求四边形ABCD的面积.
 20. 在一个箱子中有三个分别标有数字1,2,3的材质、大小都相同的小球,从中任意摸出一个小球,记下小球的数字x后,放回箱中并摇匀,再摸出一个小球,又记下小球的数字y.以先后记下的两个数字(x,y)作为点P的坐标.(1)、用列表或画树状图,求点P的横坐标与纵坐标的和为4的概率;(2)、求点P落在以坐标原点为圆心、 为半径的圆的内部的概率.21. 如图,一次函数y=kx+b的图象与反比例函数 的图象交于A(﹣3,1),B(2,n)两点,直线AB分交x轴、y轴于D,C两点.
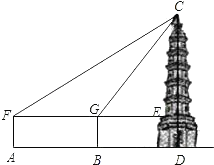
20. 在一个箱子中有三个分别标有数字1,2,3的材质、大小都相同的小球,从中任意摸出一个小球,记下小球的数字x后,放回箱中并摇匀,再摸出一个小球,又记下小球的数字y.以先后记下的两个数字(x,y)作为点P的坐标.(1)、用列表或画树状图,求点P的横坐标与纵坐标的和为4的概率;(2)、求点P落在以坐标原点为圆心、 为半径的圆的内部的概率.21. 如图,一次函数y=kx+b的图象与反比例函数 的图象交于A(﹣3,1),B(2,n)两点,直线AB分交x轴、y轴于D,C两点.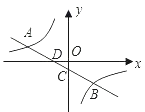 (1)、求上述反比例函数和一次函数的解析式;(2)、求 的值.22. 在一次数学活动课上,老师带领同学们去测量一座古塔CD的高度.他们首先从A处安置测倾器,测得塔顶C的仰角∠CFE=21°,然后往塔的方向前进50米到达B处,此时测得仰角∠CGE=37°,已知测倾器高1.5米,请你根据以上数据计算出古塔CD的高度.
(1)、求上述反比例函数和一次函数的解析式;(2)、求 的值.22. 在一次数学活动课上,老师带领同学们去测量一座古塔CD的高度.他们首先从A处安置测倾器,测得塔顶C的仰角∠CFE=21°,然后往塔的方向前进50米到达B处,此时测得仰角∠CGE=37°,已知测倾器高1.5米,请你根据以上数据计算出古塔CD的高度.(参考数据:sin37°≈ ,tan37°≈ ,sin21°≈ ,tan21°≈ )
 23. 某农户生产经销一种农副产品,已知这种产品的成本价为20元/千克.市场调查发现,该产品每天的销售量w (千克)与销售价x(元/千克)有如下关系:w=﹣2x+80.设这种产品每天的销售利润为y(元).(1)、求y与x之间的函数关系式.(2)、当销售价定为多少元时,每天的销售利润最大?最大利润是多少?(3)、如果物价部门规定这种产品的销售价不得高于28元/千克,该农户每天能否获得比150元更大的利润?如果能请求出最大利润,如果不能请说明理由.24. 如图,两个同心圆的圆心是O,大圆的半径为13,小圆的半径为5,AD是大圆的直径.大圆的弦AB,BE分别与小圆相切于点C,F.AD,BE相交于点G,连接BD.
23. 某农户生产经销一种农副产品,已知这种产品的成本价为20元/千克.市场调查发现,该产品每天的销售量w (千克)与销售价x(元/千克)有如下关系:w=﹣2x+80.设这种产品每天的销售利润为y(元).(1)、求y与x之间的函数关系式.(2)、当销售价定为多少元时,每天的销售利润最大?最大利润是多少?(3)、如果物价部门规定这种产品的销售价不得高于28元/千克,该农户每天能否获得比150元更大的利润?如果能请求出最大利润,如果不能请说明理由.24. 如图,两个同心圆的圆心是O,大圆的半径为13,小圆的半径为5,AD是大圆的直径.大圆的弦AB,BE分别与小圆相切于点C,F.AD,BE相交于点G,连接BD.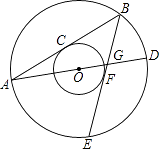 (1)、求BD的长;(2)、求∠ABE+2∠D的度数;(3)、求 的值.25. 已知矩形ABCD中,AD=6,AB=12,P为边CD上的动点,过A点作AQ⊥AP,交CB的延长线于点Q,交AB于点E,若DP=x,CQ=y,
(1)、求BD的长;(2)、求∠ABE+2∠D的度数;(3)、求 的值.25. 已知矩形ABCD中,AD=6,AB=12,P为边CD上的动点,过A点作AQ⊥AP,交CB的延长线于点Q,交AB于点E,若DP=x,CQ=y,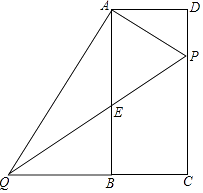 (1)、试写出y与x的函数关系式.(2)、当x为何值时,△APE为等腰直角三角形?(3)、直接写出P点由D向C运动过程中,PQ的中点F运动的路径的长?26. 已知二次函数y=ax2﹣(3a+1)x+2a+1 (a≠0),与x轴交与A(x1 , 0)B(x2 , 0)两点,与y轴交与C点.(1)、求出该函数的图象经过的定点的坐标.(2)、若A为(1)中所求的某一定点,且x1、x2 , 之间的整数恰有3个(不包括x1、x2),试求a的取值范围.(3)、当a= 时,将与x轴重合的直线绕着D(﹣5,0)逆时针旋转得到直线l:y=kx+b,过点C、B分别作l的垂线段,距离为d1、d2 , 试分别求出当|d1﹣d2|最大和最小时b的值.
(1)、试写出y与x的函数关系式.(2)、当x为何值时,△APE为等腰直角三角形?(3)、直接写出P点由D向C运动过程中,PQ的中点F运动的路径的长?26. 已知二次函数y=ax2﹣(3a+1)x+2a+1 (a≠0),与x轴交与A(x1 , 0)B(x2 , 0)两点,与y轴交与C点.(1)、求出该函数的图象经过的定点的坐标.(2)、若A为(1)中所求的某一定点,且x1、x2 , 之间的整数恰有3个(不包括x1、x2),试求a的取值范围.(3)、当a= 时,将与x轴重合的直线绕着D(﹣5,0)逆时针旋转得到直线l:y=kx+b,过点C、B分别作l的垂线段,距离为d1、d2 , 试分别求出当|d1﹣d2|最大和最小时b的值.