2017年山东省德州市陵城区中考数学模拟试卷
试卷日期:2017-07-25 考试类型:中考模拟
一、选择题
-
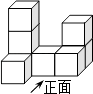
1. ﹣ 的倒数是( )A、 B、 C、﹣ D、﹣2. PM2.5是指大气中直径小于或等于0.0000025m的颗粒物,将0.0000025用科学记数法表示为( )A、0.25×10﹣5 B、0.25×10﹣6 C、2.5×10﹣5 D、2.5×10﹣63. 下列各式:①a0=1;②a2•a3=a5;③2﹣2=﹣;④﹣(3﹣5)+(﹣2)4÷8×(﹣1)=0;⑤x2+x2=2x2 , 其中正确的是( )A、①②③ B、①③⑤ C、②③④ D、②④⑤4. 如图是由八个相同小正方体组合而成的几何体,则其左视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 5. 若等腰三角形的周长是100cm,则能反映这个等腰三角形的腰长y(cm)与底边长x(cm)之间的函数关系式的图象是( )A、
5. 若等腰三角形的周长是100cm,则能反映这个等腰三角形的腰长y(cm)与底边长x(cm)之间的函数关系式的图象是( )A、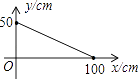 B、
B、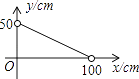 C、
C、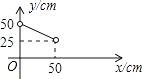 D、
D、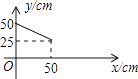 6. 如果不等式 的解集是x<2,那么m的取值范围是( )A、m=2 B、m>2 C、m<2 D、m≥27. 已知:线段AB,BC,∠ABC=90°.求作:矩形ABCD.以下是甲、乙两同学的作业:
6. 如果不等式 的解集是x<2,那么m的取值范围是( )A、m=2 B、m>2 C、m<2 D、m≥27. 已知:线段AB,BC,∠ABC=90°.求作:矩形ABCD.以下是甲、乙两同学的作业:
对于两人的作业,下列说法正确的是( )
A、两人都对 B、两人都不对 C、甲对,乙不对 D、甲不对,乙对8. 如图,△ABO缩小后变为△A′B′O,其中A、B的对应点分别为A′、B′点A、B、A′、B′均在图中在格点上.若线段AB上有一点P(m,n),则点P在A′B′上的对应点P′的坐标为( )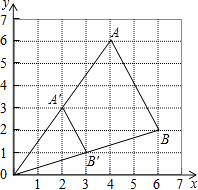 A、( ,n) B、(m,n) C、(m, ) D、( )9. 某校九年级开展“光盘行动”宣传活动,各班级参加该活动的人数统计结果如下表,对于这组统计数据,下列说法中正确的是( )
A、( ,n) B、(m,n) C、(m, ) D、( )9. 某校九年级开展“光盘行动”宣传活动,各班级参加该活动的人数统计结果如下表,对于这组统计数据,下列说法中正确的是( )班级
1班
2班
3班
4班
5班
6班
人数
52
60
62
54
58
62
A、平均数是58 B、中位数是58 C、极差是40 D、众数是6010. 如图,PA、PB是⊙O的切线,A、B是切点,点C是劣弧AB上的一个动点,若∠P=40°,则∠ACB的度数是( )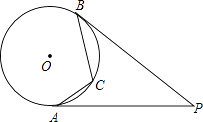 A、80° B、110° C、120° D、140°11. 设点A(x1 , y1)和B(x2 , y2)是反比例函数y= 图象上的两个点,当x1<x2<0时,y1<y2 , 则一次函数y=﹣2x+k的图象不经过的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限12. 如图,∠BAC=∠DAF=90°,AB=AC,AD=AF,点D、E为BC边上的两点,且∠DAE=45°,连接EF、BF,则下列结论:
A、80° B、110° C、120° D、140°11. 设点A(x1 , y1)和B(x2 , y2)是反比例函数y= 图象上的两个点,当x1<x2<0时,y1<y2 , 则一次函数y=﹣2x+k的图象不经过的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限12. 如图,∠BAC=∠DAF=90°,AB=AC,AD=AF,点D、E为BC边上的两点,且∠DAE=45°,连接EF、BF,则下列结论:①△AED≌△AEF;②△ABE∽△ACD;③BE+DC>DE;④BE2+DC2=DE2 , 其中正确的有( )个.
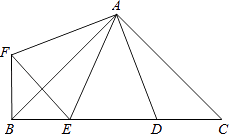 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
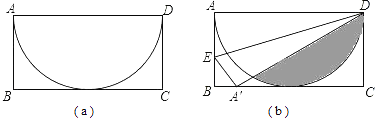
13. 计算 的结果是 .14. 有六张分别印有三角形、正方形、等腰梯形、正五边形、矩形、正六边形图案的卡片(这些卡片除图案不同外,其余均相同).现将有图案的一面朝下任意摆放,从中任意抽取一张,抽到卡片的图案既是中心对称图形,又是轴对称图形的概率为 .15. 若|b﹣1|+ =0,且一元二次方程kx2+ax+b=0有实数根,则k的取值范围是 .16. 如图(a),有一张矩形纸片ABCD,其中AD=6cm,以AD为直径的半圆,正好与对边BC相切,将矩形纸片ABCD沿DE折叠,使点A落在BC上,如图(b).则半圆还露在外面的部分(阴影部分)的面积为 .
 17.
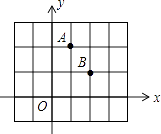
17.点A、B均在由面积为1的相同小矩形组成的网格的格点上,建立平面直角坐标系如图所示.若P是x轴上使得|PA﹣PB|的值最大的点,Q是y轴上使得QA+QB的值最小的点,则OP•OQ= .
三、解答题
-
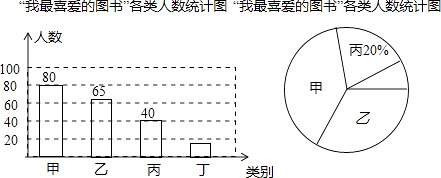
18. 先化简,再求值: ,其中a= +2.19. 在我市中小学生“我的中国梦”读书活动中,某校对部分学生做了一次主题为“我最喜爱的图书”的调查活动,将图书分为甲、乙、丙、丁四类,学生可根据自己的爱好任选其中一类.学校根据调查情况进行了统计,并绘制了不完整的条形统计图和扇形统计图.
请你结合图中信息,解答下列问题:
(1)、本次共调查了名学生;(2)、被调查的学生中,最喜爱丁类图书的有人,最喜爱甲类图书的人数占本次被调查人数的 %;(3)、在最喜爱丙类学生的图书的学生中,女生人数是男生人数的1.5倍,若这所学校共有学生1500人,请你估计该校最喜爱丙类图书的女生和男生分别有多少人.20.如图,在活动课上,小明和小红合作用一副三角板来测量学校旗杆高度.已知小明的眼睛与地面的距离(AB)是1.7m,他调整自己的位置,设法使得三角板的一条直角边保持水平,且斜边与旗杆顶端M在同一条直线上,测得旗杆顶端M仰角为45°;小红眼睛与地面的距离(CD)是1.5m,用同样的方法测得旗杆顶端M的仰角为30°.两人相距28米且位于旗杆两侧(点B、N、D在同一条直线上).求出旗杆MN的高度.(参考数据: , ,结果保留整数.)
 21. 某汽车租赁公司拥有20辆汽车.据统计,当每辆车的日租金为400元时,可全部租出;当每 辆车的日租金每增加50元,未租出的车将增加1辆;公司平均每日的各项支出共4800元.设公司每日租出x辆车时,日收益为y元.(日收益=日租金收入一平均每日各项支出)(1)、公司每日租出x辆车时,每辆车的日租金为元(用含x的代数式表示);(2)、当每日租出多少辆时,租赁公司日收益最大?最大是多少元?(3)、当每日租出多少辆时,租赁公司的日收益不盈也不亏?22. 已知直线PD垂直平分⊙O的半径OA于点B,PD交⊙O于点C、D,PE是⊙O的切线,E为切点,连结AE,交CD于点F.
21. 某汽车租赁公司拥有20辆汽车.据统计,当每辆车的日租金为400元时,可全部租出;当每 辆车的日租金每增加50元,未租出的车将增加1辆;公司平均每日的各项支出共4800元.设公司每日租出x辆车时,日收益为y元.(日收益=日租金收入一平均每日各项支出)(1)、公司每日租出x辆车时,每辆车的日租金为元(用含x的代数式表示);(2)、当每日租出多少辆时,租赁公司日收益最大?最大是多少元?(3)、当每日租出多少辆时,租赁公司的日收益不盈也不亏?22. 已知直线PD垂直平分⊙O的半径OA于点B,PD交⊙O于点C、D,PE是⊙O的切线,E为切点,连结AE,交CD于点F.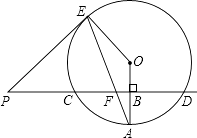 (1)、若⊙O的半径为8,求CD的长;(2)、证明:PE=PF;(3)、若PF=13,sinA= ,求EF的长.23. 联想三角形外心的概念,我们可引入如下概念.
(1)、若⊙O的半径为8,求CD的长;(2)、证明:PE=PF;(3)、若PF=13,sinA= ,求EF的长.23. 联想三角形外心的概念,我们可引入如下概念.定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.
举例:如图1,若PA=PB,则点P为△ABC的准外心.
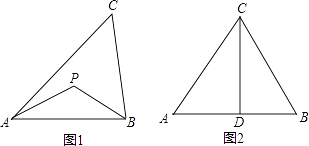 (1)、应用:如图2,CD为等边三角形ABC的高,准外心P在高CD上,且PD= AB,求∠APB的度数.
(1)、应用:如图2,CD为等边三角形ABC的高,准外心P在高CD上,且PD= AB,求∠APB的度数.
(2)、探究:已知△ABC为直角三角形,斜边BC=5,AB=3,准外心P在AC边上,试探究PA的长.24.如图,抛物线y= x2+bx+c与y轴交于点C(0,﹣4),与x轴交于点A,B,且B点的坐标为(2,0).
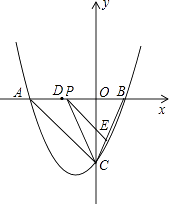 (1)、求该抛物线的解析式.(2)、若点P是AB上的一动点,过点P作PE∥AC,交BC于E,连接CP,求△PCE面积的最大值.(3)、若点D为OA的中点,点M是线段AC上一点,且△OMD为等腰三角形,求M点的坐标.
(1)、求该抛物线的解析式.(2)、若点P是AB上的一动点,过点P作PE∥AC,交BC于E,连接CP,求△PCE面积的最大值.(3)、若点D为OA的中点,点M是线段AC上一点,且△OMD为等腰三角形,求M点的坐标.