2017年上海市中考数学试卷

试卷日期：2017-07-13 考试类型：中考真卷

前去【出卷网】下载

一、选择题

1. 下列实数中，无理数是（）

A、0 B、 $\sqrt{2}$ C、﹣2 D、 $\frac{2}{7}$

查看试题解析
2. 下列方程中，没有实数根的是（）

A、x²﹣2x=0 B、x²﹣2x﹣1=0 C、x²﹣2x+1=0 D、x²﹣2x+2=0

查看试题解析
3. 如果一次函数y=kx+b（k、b是常数，k≠0）的图象经过第一、二、四象限，那么k、b应满足的条件是（）

A、k＞0，且b＞0 B、k＜0，且b＞0 C、k＞0，且b＜0 D、k＜0，且b＜0

查看试题解析
4. 数据2、5、6、0、6、1、8的中位数和众数分别是（）

A、0和6 B、0和8 C、5和6 D、5和8

查看试题解析
5. 下列图形中，既是轴对称又是中心对称图形的是（）

A、菱形 B、等边三角形 C、平行四边形 D、等腰梯形

查看试题解析
6. 已知平行四边形ABCD，AC、BD是它的两条对角线，那么下列条件中，能判断这个平行四边形为矩形的是（）

A、∠BAC=∠DCA B、∠BAC=∠DAC C、∠BAC=∠ABD D、∠BAC=∠ADB

查看试题解析

二、填空题

7. 计算：2a•a²= ．

查看试题解析
8. 不等式组 ${\begin{matrix} 2 x > 6 \\ x - 2 > 0 \end{matrix}$ 的解集是．

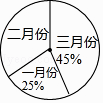
查看试题解析
9. 方程 $\sqrt{2 x - 3}$ =1的解是．

查看试题解析
10. 如果反比例函数y= $\frac{k}{x}$ （k是常数，k≠0）的图象经过点（2，3），那么在这个函数图象所在的每个象限内，y的值随x的值增大而．（填“增大”或“减小”）

查看试题解析
11. 某市前年PM2.5的年均浓度为50微克/立方米，去年比前年下降了10%，如果今年PM2.5的年均浓度比去年也下降10%，那么今年PM2.5的年均浓度将是微克/立方米．

查看试题解析
12. 不透明的布袋里有2个黄球、3个红球、5个白球，它们除颜色外其它都相同，那么从布袋中任意摸出一球恰好为红球的概率是．

查看试题解析
13. 已知一个二次函数的图象开口向上，顶点坐标为（0，﹣1 ），那么这个二次函数的解析式可以是．（只需写一个）

查看试题解析
14.
某企业今年第一季度各月份产值占这个季度总产值的百分比如图所示，又知二月份产值是72万元，那么该企业第一季度月产值的平均数是万元．

查看试题解析
15. 如图，已知AB∥CD，CD=2AB，AD、BC相交于点E，设 $\vec{A E}$ = $\vec{a}$ ， $\vec{C E}$ = $\vec{b}$ ，那么向量 $\vec{C D}$ 用向量 $\vec{a}$ 、 $\vec{b}$ 表示为．

查看试题解析
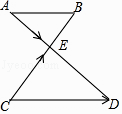16. 一副三角尺按如图的位置摆放（顶点C 与F 重合，边CA与边FE叠合，顶点B、C、D在一条直线上）．将三角尺DEF绕着点F按顺时针方向旋转n°后（0＜n＜180 ），如果EF∥AB，那么n的值是．

查看试题解析
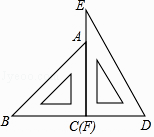17. 如图，已知Rt△ABC，∠C=90°，AC=3，BC=4．分别以点A、B为圆心画圆．如果点C在⊙A内，点B在⊙A外，且⊙B与⊙A内切，那么⊙B的半径长r的取值范围是．

查看试题解析
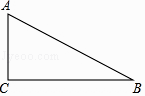18. 我们规定：一个正n边形（n为整数，n≥4）的最短对角线与最长对角线长度的比值叫做这个正n边形的“特征值”，记为λ_n ，那么λ₆= ．

查看试题解析

三、解答题

19. 计算： $\sqrt{18}$ +（ $\sqrt{2}$ ﹣1）²﹣9 $^{\frac{1}{2}}$ +（ $\frac{1}{2}$ ）^﹣1 ．

查看试题解析
20. 解方程： $\frac{3}{x^{2} - 3 x}$ ﹣ $\frac{1}{x - 3}$ =1．

查看试题解析
21.
如图，一座钢结构桥梁的框架是△ABC，水平横梁BC长18米，中柱AD高6米，其中D是BC的中点，且AD⊥BC．

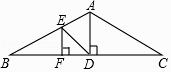(1)、求sinB的值；

(2)、现需要加装支架DE、EF，其中点E在AB上，BE=2AE，且EF⊥BC，垂足为点F，求支架DE的长．

查看试题解析
22. 甲、乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案．
甲公司方案：每月的养护费用y（元）与绿化面积x（平方米）是一次函数关系，如图所示．
乙公司方案：绿化面积不超过1000平方米时，每月收取费用5500 元；绿化面积超过1000平方米时，每月在收取5500元的基础上，超过部分每平方米收取4元．

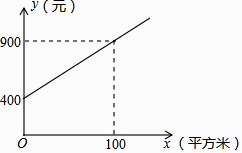(1)、求如图所示的y与x的函数解析式：（不要求写出定义域）；

(2)、如果某学校目前的绿化面积是1200平方米，试通过计算说明：选择哪家公司的服务，每月的绿化养护费用较少．

查看试题解析
23.
已知：如图，四边形ABCD中，AD∥BC，AD=CD，E是对角线BD上一点，且EA=EC．

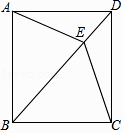(1)、求证：四边形ABCD是菱形；

(2)、如果BE=BC，且∠CBE：∠BCE=2：3，求证：四边形ABCD是正方形．

查看试题解析
24.
已知在平面直角坐标系xOy中（如图），已知抛物线y=﹣x²+bx+c经过点A（2，2），对称轴是直线x=1，顶点为B．

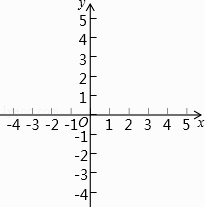(1)、求这条抛物线的表达式和点B的坐标；

(2)、点M在对称轴上，且位于顶点上方，设它的纵坐标为m，联结AM，用含m的代数式表示∠AMB的余切值；

(3)、将该抛物线向上或向下平移，使得新抛物线的顶点C在x轴上．原抛物线上一点P平移后的对应点为点Q，如果OP=OQ，求点Q的坐标．

查看试题解析
25.
如图，已知⊙O的半径长为1，AB、AC是⊙O的两条弦，且AB=AC，BO的延长线交AC于点D，联结OA、OC．

(1)、求证：△OAD∽△ABD；

(2)、当△OCD是直角三角形时，求B、C两点的距离；

(3)、记△AOB、△AOD、△COD 的面积分别为S₁、S₂、S₃ ，如果S₂是S₁和S₃的比例中项，求OD的长．

查看试题解析