2017年上海市徐汇区中考数学二模试卷

试卷日期：2017-06-29 考试类型：中考模拟

前去【出卷网】下载

一、选择题

1. 如果数轴上表示2和﹣4的两点分别是点A和点B，那么点A和点B之间的距离是（）

A、﹣2 B、2 C、﹣6 D、6．

查看试题解析
2. 已知点M（1﹣2m，m﹣1）在第四象限内，那么m的取值范围是（）

A、m＞1 B、m＜ $\frac{1}{2}$ C、 $\frac{1}{2}$ ＜m＜1 D、m＜ $\frac{1}{2}$ 或m＞1

查看试题解析
3. 如图，AB∥CD，BE平分∠ABC，∠C=36°，那么∠ABE的大小是（）

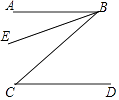A、18° B、24° C、36° D、54°．

查看试题解析
4. 已知直线y=ax+b（a≠0）经过点A（﹣3，0）和点B（0，2），那么关于x的方程ax+b=0的解是（）

A、x=﹣3 B、x=﹣1 C、x=0 D、x=2

查看试题解析
5. 某校开展“阅读季”活动，小明调查了班级里40名同学计划购书的花费情况，并将结果绘制成如图所示的条形统计图，根据图中相关信息，这次调查获取的样本数据的众数和中位数分别是（）

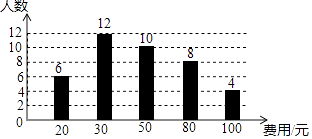A、12和10 B、30和50 C、10和12 D、50和30．

查看试题解析
6. 如图，在△ABC中，AC=BC，点D、E分别是边AB、AC的中点，延长DE到F，使得EF=DE，那么四边形ADCF是（）

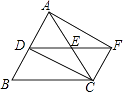A、等腰梯形 B、直角梯形 C、矩形 D、菱形

查看试题解析

二、填空题

7. 人体中成熟的红细胞的平均直径为0.0000077m，0.0000077用科学记数法表示为．

查看试题解析
8. 方程 $\sqrt{x^{2} - x}$ = $\sqrt{2}$ 的解是．

查看试题解析
9. 如果反比例函数y= $\frac{k}{x}$ （k≠0）的图象经过点P（﹣1，4），那么k的范围是．

查看试题解析
10. 如果关于x的方程x²+3x﹣k=0有两个不相等的实数根，那么k的取值范围是．

查看试题解析
11. 将抛物线y=x²﹣2x+1向上平移2个单位后，所得抛物线的顶点坐标是．

查看试题解析
12. 在实数 $\sqrt{5}$ ，π，3°，tan60°，2中，随机抽取一个数，抽得的数大于2的概率是．

查看试题解析
13. 甲，乙，丙，丁四名跳高运动员赛前几次选拔赛成绩如表所示，根据表中的信息，如果要从中，选择一名成绩好又发挥稳定的运动员参加比赛，那么应选．
甲
乙
丙
丁
平均数（cm）
185
180
185
180
方差
3.6
3.6
7.9
8.2

查看试题解析
14. 如果t是方程x²﹣2x﹣1=0的根，那么代数式2t²﹣4t的值是．

查看试题解析
15. 如图，四边形DEFG是△ABC的内接矩形，其中D、G分别在边AB，AC上，点E、F在边BC上，DG=2DE，AH是△ABC的高，BC=20，AH=15，那么矩形DEFG的周长是．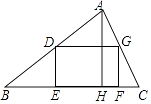

查看试题解析
16. 如图，在平行四边形ABCD中，AE⊥CD，垂足为E，AF⊥BC，垂足为F，AD=4，BF=3，∠EAF=60°，设 $\vec{A B}$ = $\vec{a}$ ，如果向量 $\vec{C E}$ =k $\vec{a}$ （k≠0），那么k的值是．

查看试题解析
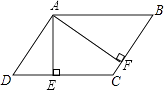17. 如图，在△ABC中，AD平分∠BAC交边BC于点D，BD=AD，AB=3，AC=2，那么AD的长是．

查看试题解析
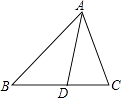18. 如图，在△ABC中，∠ACB=α（90°＜α＜180°），将△ABC绕着点A逆时针旋转2β（0°＜β＜90°）后得△AED，其中点E、D分别和点B、C对应，联结CD，如果CD⊥ED，请写出一个关于α与β的等量关系的式子．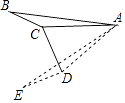

查看试题解析

三、解答题

19. 先化简，再求值： $\frac{a^{2} - 3 a}{a^{2} + a}$ ÷ $\frac{a - 3}{a^{2} - 1}$ ﹣ $\frac{3 a + 3}{a + 1}$ （其中a= $\frac{1}{\sqrt{2} - 1}$ ）

查看试题解析
20. 解方程组： ${\begin{matrix} x - 2 y = 3 \\ 4 x^{2} - 12 x y + 9 y^{2} = 16 \end{matrix}$ ．

查看试题解析
21. 某足球特色学校在商场购买甲、乙两种品牌的足球．已知乙种足球比甲种足球每只贵20元，该校分别花费2000元、1400元购买甲、乙两种足球，这样购得甲种足球的数量是购得乙种足球数量的2倍，求甲、乙两种足球的单价各是多少元？

查看试题解析
22. 如图，已知梯形ABCD中，ADǁBC，AC、BD相交于点O，AB⊥AC，AD=CD，AB=3，BC=5．求：

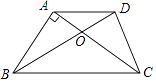(1)、tan∠ACD的值；

(2)、梯形ABCD的面积．

查看试题解析
23. 如图1，在Rt△ABC中，∠ACB=90°，点D是边AB的中点，点E在边BC上，AE=BE，点M是AE的中点，联结CM，点G在线段CM上，作∠GDN=∠AEB交边BC于N．

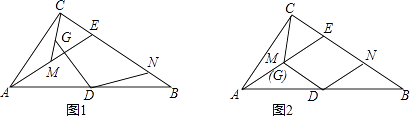(1)、如图2，当点G和点M重合时，求证：四边形DMEN是菱形；

(2)、如图1，当点G和点M、C不重合时，求证：DG=DN．

查看试题解析
24.
如图，已知抛物线y=ax²+4（a≠0）与x轴交于点A和点B（2，0），与y轴交于点C，点D是抛物线在第一象限的点．

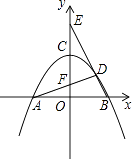(1)、当△ABD的面积为4时，
①求点D的坐标；
②联结OD，点M是抛物线上的点，且∠MDO=∠BOD，求点M的坐标；

(2)、直线BD、AD分别与y轴交于点E、F，那么OE+OF的值是否变化，请说明理由．

查看试题解析
25. 如图，已知△ABC中，AB=AC=5，BC=6，点O是边BC上的动点，以点O为圆心，OB为半径作圆O，交AB边于点D，过点D作∠ODP=∠B，交边AC于点P，交圆O与点E．设OB=x．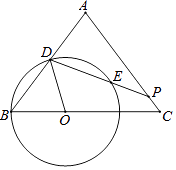

(1)、当点P与点C重合时，求PD的长；

(2)、设AP﹣EP=y，求y关于x的解析式及定义域；

(3)、联结OP，当OP⊥OD时，试判断以点P为圆心，PC为半径的圆P与圆O的位置关系．

查看试题解析

	甲	乙	丙	丁
平均数（cm）	185	180	185	180
方差	3.6	3.6	7.9	8.2