2017年上海市长宁区、嘉定区高考数学一模试卷

试卷日期：2017-04-27 考试类型：高考模拟

前去【出卷网】下载

一、填空题

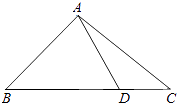
1. 设集合A={x||x﹣2|＜1，x∈R}，集合B=Z，则A∩B= ．

查看试题解析
2. 函数y=sin（ωx﹣ $\frac{π}{3}$ ）（ω＞0）的最小正周期是π，则ω= ．

查看试题解析
3. 设i为虚数单位，在复平面上，复数 $\frac{3}{{(2 - i)}^{2}}$ 对应的点到原点的距离为．

查看试题解析
4. 若函数f（x）=log₂（x+1）+a的反函数的图象经过点（4，1），则实数a= ．

查看试题解析
5. 已知（a+3b）ⁿ展开式中，各项系数的和与各项二项式系数的和之比为64，则n= ．

查看试题解析
6. 甲、乙两人从5门不同的选修课中各选修2门，则甲、乙所选的课程中恰有1门相同的选法有种．

查看试题解析
7. 若圆锥的侧面展开图是半径为2cm，圆心角为270°的扇形，则这个圆锥的体积为 cm³ ．

查看试题解析
8. 若数列{a_n}的所有项都是正数，且 $\sqrt{a_{1}}$ + $\sqrt{a_{2}}$ +…+ $\sqrt{a_{n}}$ =n²+3n（n∈N^*），则 $\lim_{n \to \infty}$ $\frac{1}{n^{2}}$ （ $\frac{a_{1}}{2} + \frac{a_{2}}{3} + \dots + \frac{a_{n}}{n + 1}$ ）= ．

查看试题解析
9. 如图，在△ABC中，∠B=45°，D是BC边上的一点，AD=5，AC=7，DC=3，则AB的长为．

查看试题解析
10. 有以下命题：

①若函数f（x）既是奇函数又是偶函数，则f（x）的值域为{0}；
②若函数f（x）是偶函数，则f（|x|）=f（x）；
③若函数f（x）在其定义域内不是单调函数，则f（x）不存在反函数；
④若函数f（x）存在反函数f^﹣¹（x），且f^﹣¹（x）与f（x）不完全相同，则f（x）与f^﹣¹（x）图象的公共点必在直线y=x上；
其中真命题的序号是．（写出所有真命题的序号）

查看试题解析
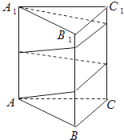
11. 设向量 $\vec{O A}$ =（1，﹣2）， $\vec{O B}$ =（a，﹣1）， $\vec{O C}$ =（﹣b，0），其中O为坐标原点，a＞0，b＞0，若A、B、C三点共线，则 $\frac{1}{a} + \frac{2}{b}$ 的最小值为．

查看试题解析
12.
如图，已知正三棱柱ABC﹣A₁B₁C₁的底面边长为2cm，高为5cm，一质点自A点出发，沿着三棱柱的侧面绕行两周到达A₁点的最短路线的长为 cm．

查看试题解析

二、选择题

13. “x＜2”是“x²＜4”的（）

A、充分非必要条件 B、必要非充分条件 C、充要条件 D、既非充分也非必要条件

查看试题解析
14. 若无穷等差数列{a_n}的首项a₁＜0，公差d＞0，{a_n}的前n项和为S_n ，则以下结论中一定正确的是（）

A、S_n单调递增 B、S_n单调递减 C、S_n有最小值 D、S_n有最大值

查看试题解析
15. 给出下列命题：

①存在实数α使 $\sin α + \cos α = \frac{3}{2}$ ．
②直线 $x = - \frac{π}{2}$ 是函数y=sinx图象的一条对称轴．
③y=cos（cosx）（x∈R）的值域是[cos1，1]．
④若α，β都是第一象限角，且α＞β，则tanα＞tanβ．
其中正确命题的题号为（）

A、①② B、②③ C、③④ D、①④

查看试题解析
16. 如果对一切实数x、y，不等式 $\frac{y}{4}$ ﹣cos²x≥asinx﹣ $\frac{9}{y}$ 恒成立，则实数a的取值范围是（）

A、（﹣∞， $\frac{4}{3}$ ] B、[3，+∞） C、[﹣2 $\sqrt{2}$ ，2 $\sqrt{2}$ ] D、[﹣3，3]

查看试题解析

三、解答题

17. 如图，已知AB⊥平面BCD，BC⊥CD，AD与平面BCD所成的角为30°，且AB=BC=2；

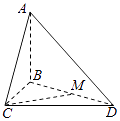(1)、求三棱锥A﹣BCD的体积；

(2)、设M为BD的中点，求异面直线AD与CM所成角的大小（结果用反三角函数值表示）．

查看试题解析
18. 在△ABC中，a，b，c分别是角A，B，C的对边，且8sin² $\frac{B + C}{2} - 2 \cos 2 A = 7$ ．

(1)、求角A的大小；

(2)、若a= $\sqrt{3}$ ，b+c=3，求b和c的值．

查看试题解析
19. 某地要建造一个边长为2（单位：km）的正方形市民休闲公园OABC，将其中的区域ODC开挖成一个池塘，如图建立平面直角坐标系后，点D的坐标为（1，2），曲线OD是函数y=ax²图象的一部分，对边OA上一点M在区域OABD内作一次函数y=kx+b（k＞0）的图象，与线段DB交于点N（点N不与点D重合），且线段MN与曲线OD有且只有一个公共点P，四边形MABN为绿化风景区：

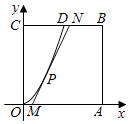(1)、求证：b=﹣ $\frac{k^{2}}{8}$ ；

(2)、设点P的横坐标为t，①用t表示M、N两点坐标；②将四边形MABN的面积S表示成关于t的函数S=S（t），并求S的最大值．

查看试题解析
20. 已知函数f（x）=9^x﹣2a•3^x+3：

(1)、若a=1，x∈[0，1]时，求f（x）的值域；

(2)、当x∈[﹣1，1]时，求f（x）的最小值h（a）；

(3)、是否存在实数m、n，同时满足下列条件：①n＞m＞3；②当h（a）的定义域为[m，n]时，其值域为[m² ， n²]，若存在，求出m、n的值，若不存在，请说明理由．

查看试题解析
21. 已知无穷数列{a_n}的各项都是正数，其前n项和为S_n ，且满足：a₁=a，rS_n=a_na_n₊₁﹣1，其中a≠1，常数r∈N；

(1)、求证：a_n₊₂﹣a_n是一个定值；

(2)、若数列{a_n}是一个周期数列（存在正整数T，使得对任意n∈N^* ，都有a_n₊_T=a_n成立，则称{a_n}为周期数列，T为它的一个周期，求该数列的最小周期；

(3)、若数列{a_n}是各项均为有理数的等差数列，c_n=2•3ⁿ^﹣¹（n∈N^*），问：数列{c_n}中的所有项是否都是数列{a_n}中的项？若是，请说明理由，若不是，请举出反例．

查看试题解析