2016年四川省高考数学适应性试卷（理科）

试卷日期：2017-01-19 考试类型：高考模拟

前去【出卷网】下载

一、选择题：

1. 已知集合M，N满足M∪N={1，2，3}，M∩N={a}，则（）

A、a=1 B、a=2 C、a=3 D、a∈M∪N

查看试题解析
2. 若不等式x²+ax+b＜0的解集为（﹣1，2），则ab的值为（）

A、﹣1 B、1 C、﹣2 D、2

查看试题解析
3. 设函数f（x）=（m+nx）³=a₀+a₁x+a₂x²+a₃x³ ， mn≠0，则 $\frac{a_{0} a_{3}}{a_{1} a_{2}}$ 的值为（）

A、 $\frac{1}{9}$ B、 $\frac{1}{6}$ C、 $\frac{1}{3}$ D、1

查看试题解析
4. 若“∃x∈[﹣1，m]（m＞﹣1），|x|﹣1＞0”是假命题，则实数m的取值范围是（）

A、（﹣1，1） B、（﹣1，1] C、[1，+∞） D、[0，1]

查看试题解析
5. 若复数z=cos $\frac{π}{12}$ +isin $\frac{π}{12}$ （i是虚数单位），复数z²的实部虚部分别为a，b，则下列结论正确的是（）

A、ab＜0 B、a²+b²≠1 C、 $\frac{a}{b} = \sqrt{3}$ D、 $\frac{b}{a} = \sqrt{3}$

查看试题解析
6. 执行如图所示的程序框图，输出的结果是（）

A、﹣2 B、 $- \frac{1}{3}$ C、 $\frac{1}{2}$ D、3

查看试题解析
7. 在△A BC中，若 $\vec{A B}$ =（1，2）， $\vec{A C}$ =（﹣2，3），则△ABC的面积为（）

A、 $\frac{7}{2}$ B、4 C、7 D、8

查看试题解析
8. 已知P，Q，R是圆x²+y²﹣2x﹣8=0上不同三点，它们到直线l：x+ $\sqrt{3}$ y+7=0的距离分别为x₁ ， x₂ ， x₃ ，若x₁ ， x₂ ， x₃成等差数列，则公差的最大值为（）

A、1 B、2 C、3 D、4

查看试题解析
9. 设P是左、右顶点分别为A，B的双曲线x²﹣y²=1上的点，若直线PA的倾斜角为 $\frac{2 π}{3}$ ，则直线PB的倾斜角是（）

A、 $\frac{π}{6}$ B、 $\frac{3 π}{4}$ C、 $\frac{5 π}{6}$ D、 $\frac{11 π}{12}$

查看试题解析
10. 设0＜a＜1，已知函数f（x）= ${\begin{matrix} - x \ln x ， 0 < x \leq a \\ \frac{1}{e} \cos 2 π x ， a < x \leq 1 \end{matrix}$ ，若对任意b∈（0， $\frac{1}{e}$ ），函数g（x）=f（x）﹣b至少有两个零点，则a的取值范围是（）

A、 $(0 ， \frac{1}{e}]$ B、 $(0 ， \frac{3}{4}]$ C、 $[\frac{1}{e} ， 1)$ D、 $[\frac{1}{e} ， \frac{3}{4}]$

查看试题解析

二、填空题

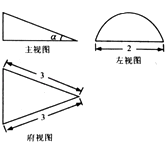
11. 若抛物线y=ax²的焦点F的坐标为（0，﹣1），则实数a的值为．

查看试题解析
12. 某几何体的三视图如图所示，其中左视图为半圆，则主视图中α角的正切值为．

查看试题解析
13. 若函数f（x）=x+ $\frac{k}{x}$ 在[1，3]上的最小值为t，若t≠2 $\sqrt{k}$ ，则正数k的取值范围为．

查看试题解析
14. 当实数a在区间[1，m]（m＞1）随机取值时，函数f（x）=﹣x²+ax+2在区间（1，+∞）上是单调减函数的概率为 $\frac{1}{3}$ ，则实数m= ．

查看试题解析
15. 已知实数a，b满足：5﹣a≤3b≤12﹣3a，e^b≤a，则 $\frac{b}{a}$ 的取值范围为．

查看试题解析

三、解答题

16. 已知数列{a_n}的前n项和S_n=k•3ⁿ﹣m，且a₁=3，a₃=27．
（I）求证：数列{a_n}是等比数列；
（II）若a_nb_n=log₃a_n₊₁ ，求数列{b_n}的前n项和T_n ．

查看试题解析
17. 为了解学生寒假阅读名著的情况，一名教师对某班级的所有学生进行了调查，调查结果如下表：
本数
人数
性别
0
1
2
3
4
5
男生
0
1
4
3
2
2
女生
0
0
1
3
3
1
（I）从这班学生中任选一名男生，一名女生，求这两名学生阅读名著本数之和为4的概率；
（II）若从阅读名著不少于4本的学生中任选4人，设选到的男学生人数为 X，求随机变量 X的分布列和数学期望；
（III）试判断男学生阅读名著本数的方差 $s_{1}^{2}$ 与女学生阅读名著本数的方差 $s_{2}^{2}$ 的大小（只需写出结论）．

查看试题解析
18. 如图ABCD是平面四边形，∠ADB=∠BCD=90°，AB=4，BD=2．
（Ⅰ）若BC=1，求AC的长；
（Ⅱ）若∠ACD=30°，求tan∠BDC的值．

查看试题解析
19. 在斜三棱柱ABC﹣A₁B₁C₁中，底面ABC是正三角形，E是AB中点，A₁E⊥平面ABC．
（I）证明：BC₁∥平面 A₁EC；
（II）若A₁A⊥A₁B，且AB=2．
①求点B到平面ACC₁A₁的距离；
②求直线CB₁与平面ACC₁A₁所成角的正弦值．

查看试题解析
20. 已知圆锥曲线 E： $\sqrt{{(x - 2 \sqrt{3})}^{2} + y^{2}} + \sqrt{{(x + 2 \sqrt{3})}^{2} + y^{2}} = 4 \sqrt{6}$ ．
（I）求曲线 E的离心率及标准方程；
（II）设 M（x₀ ， y₀）是曲线 E上的任意一点，过原点作⊙M：（x﹣x₀）²+（y﹣y₀）²=8的两条切线，分别交曲线 E于点 P、Q．
①若直线OP，OQ的斜率存在分别为k₁ ， k₂ ，求证：k₁k₂=﹣ $\frac{1}{2}$ ；
②试问OP²+OQ²是否为定值．若是求出这个定值，若不是请说明理由．

查看试题解析
21. 设函数f（x）=e^x ， g（x）=kx+1．
（I）求函数y=f（x）﹣（x+1）的最小值；
（II）证明：当k＞1时，存在x₀＞0，使对于任意x∈（0，x₀）都有f（x）＜g（x）；
（III）若存在实数m使对任意x∈（0，m）都有|f（x）﹣g（x）|＞x成立，求实数k的取值范围．

查看试题解析